福建省莆田市名校2022-2023学年高二下学期期中考试数学(B卷)试题(PDF版含答案)
文档属性
| 名称 | 福建省莆田市名校2022-2023学年高二下学期期中考试数学(B卷)试题(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 20:56:03 | ||
图片预览




文档简介
莆田名校 2022- 2023学年高二期下学期期中考 (B卷)
数 学 试 题
本试卷共 4页 全卷满分 150分 考试用时 120分钟
一、单选题 (本大题共 8小题,共 40分)
1.甲、乙两个元件构成一并联电路,设E=“甲元件故障”,F=“乙元件故障”,则表示电路故障的事件
为 ( )
A. E∪F B. E∪F C. E∩F D. E∩F
2.在 a和 b两数之间插入n个数,使它们与 a,b组成等差数列,则该数列的公差为 ( )
A. b- an+ 1 B.
b- a C. b- an n+ 2 D.
a- b
n+ 2
3.已知某运动员每次射击击中目标的概率为 80%.现采用随机模拟的方法估计某运动员射击 4次,至
少击中 3次的概率.先由计算器给出 0到 9之间取整数值的随机数,指定 0,1表示没有击中目标,
2,3,4,5,6,7,8,9表示击中目标,以 4个随机数为一组,代表射击 4次的结果,经随机模拟产生
了 20组随机数:
7527 0293 7140 9857 0347 4373 8636
6947 7610 4281 1417 4698 0371 6233
2616 8045 6011 3661 9597 7424
根据以上数据估计该射击运动员射击 4次,至少击中 3次的概率为 ( )
A. 0.8 B. 0.75 C. 0.7 D. 0.65
4.某单位入职面试中有三道题目,有三次答题机会,一旦某次答对抽到的题目,则面试通过,否则就一
直抽题到第 3次为止.若求职者小王答对每道题目的概率都是 0.7,则他最终通过面试的概率为
( )
A. 0.7 B. 0.91 C. 0.973 D. 0.981
y2
5.已知双曲线E:x2- 3 = 1的左焦点为F,过点F作双曲线E的一条渐近线的垂线(垂足为B)交另
一条渐近线于点C,则线段BC的长度为 ( )
A. 1 B. 3 C. 2 D. 2 3
2 y2
6.设F1,F2分别为椭圆C: x2 + 2 = 1(a> b> 0)的左、右焦点,点A,B在C上,若F1A= 2BF1,2|F2B|a b
= 5|F1A|,则椭圆C的离心率为 ( )
A. 2 62 B. 4 C.
5 D. 103 5
·1·
7.图 1所示,抛物面天线是指由抛物面 (抛物线绕其对称轴旋转形成的曲面)反射器和位于焦点上的
照射器 (馈源,通常采用喇叭天线)组成的单反射面型天线,广泛应用于微波和卫星通讯等领域,具
有结构简单、方向性强、工作频带宽等特点.图 2是图
1的轴截面,A,B两点关于抛物线的对称轴对称,F是
抛物线的焦点,∠AFB是馈源的方向角,记为 θ,焦点F
f
到顶点的距离 f与口径 d的比值 称为抛物面天线的
d
焦径比,它直接影响天线的效率与信噪比等.如果某抛
物面天线馈源的方向角 θ满足 tanθ=-4 5,则其焦径
图 1 图 2
比为 ( )
A. 5 10 10 54 B. 4 C. 8 D. 8
8.在编号分别为 (i= 0,1,2,…,n- 1)的 n名同学中挑选一人参加某项活动,挑选方法如下:抛掷两枚
骰子,将两枚骰子的点数之和除以 n所得的余数如果恰好为 i,则选编号为 i的同学.下列哪种情况
是不 公 平 的挑选方法 ( )
A. n= 2 B. n= 3 C. n= 4 D. n= 6
二、多选题 (本大题共 4小题,共 20分,每道题全部选对的得 5分,部分选对得 2分,有选错得 0分.)
9.设A,B是两个随机事件,则下列说法正确的有 ( )
A. AB+AB表示两个事件至少有一个发生 B. A+B表示两个事件至少有一个发生
C. A+B表示两个事件均不发生 D. A B表示两个事件均不发生
10.某班级体温检测员对一周内甲 乙两名同学的体温进行了统计,其结果如图所示,则下列说法正确
的有 ( )
A. 乙同学体温的极差为 0.2℃
B. 乙同学体温的众数为 36.4℃,中位数与平均数相等
C. 甲同学的体温比乙同学的体温稳定
D. 甲同学体温的第 70百分位数为 36.6℃
11.抛掷一红一绿两枚质地均匀的骰子,记下骰子朝上面的点数.用 x表示红色骰子的点数,用 y表示绿
色骰子的点数,用 (x,y)表示一次试验的结果.定义事件:A=“x+ y= 7”,事件B=“xy为奇数”,
事件C=“x> 3”,则下列结论正确的有 ( )
A. A与B互斥但不对立 B. A与B对立
C. A与C相互独立 D. B与C相互独立
12.已知抛物线 E:y2= 4x的焦点为 F,准线交 x 轴于点 C ,直线 l 过 C 且交 E 于不同的A,B 两
点,且CA= λCB(λ> 1),下列命题正确的有 ( )
A. 直线 l的斜率 k∈ (-1,0) ∪ (0,1) B. 3若 |BF| = 2 ,则 |AF| = 4
C. 若 λ= 2,则 |AF| = 2|BF| D. 存在 λ使得BF平分∠AFC
·2·
三、填空题 (本大题共 4小题,共 20分)
13.从 5张分别写有 1,2,3,4,5的卡片中不放回随机抽取 2张,则抽到的 2张卡片上的数字之积是偶
数的概率为 .
14.袋子中有 6个大小质地相同的球,其中 3个红球,3个黄球,从中不放回随机取出 3个球,
则概率大于 0且与事件“至多取出一个黄球”互斥不对立的事件可以是 .
15.在平面直角坐标系 xOy中,A(6,0), B(6,1)点P满足 |PO| = 2|PA|,
则动点P的运动轨迹方程为 ,|PB| +2|PA|的最小值为 .
16. 若已知 30个数 x1,x2, ,x30的平均数为 6,方差为 9;现从原 30个数中剔除 x1,x2, ,x10这 10个数,且
剔除的这 10个数的平均数为 8,方差为 5,则剩余的 20个数 x11,x12, ,x30的方差为 .
四、解答题 (本大题共 6小题,共 70分)
17. (9分)设等比数列 {an}的前n项和为Sn,且 a4- a1= 7,S3= 7.
(1)求数列 {an}的通项公式;
an,n为偶数,(2)设 bn= 数列 {bn}的前 2n项和为T, 2n,求T2n.log2an n为奇数,
18. (11分) 树人中学为了学生的身心健康,加强食堂用餐质量 (简称“美食”)的过程中,后勤部门需了
认可程度平均分
解学生对“美食”工作的认可程度,若学生认可系数 (认可系数= 100 )不低于 0.85,
“美食”工作按原方案继续实施,否则需进一步整改. 为此该部门随机调查了 600 名学生,根据这
600名学生对“美食”工作认可程度给出的评分,分成 [50,60),[60,70),[70,80),[80,90),[90,
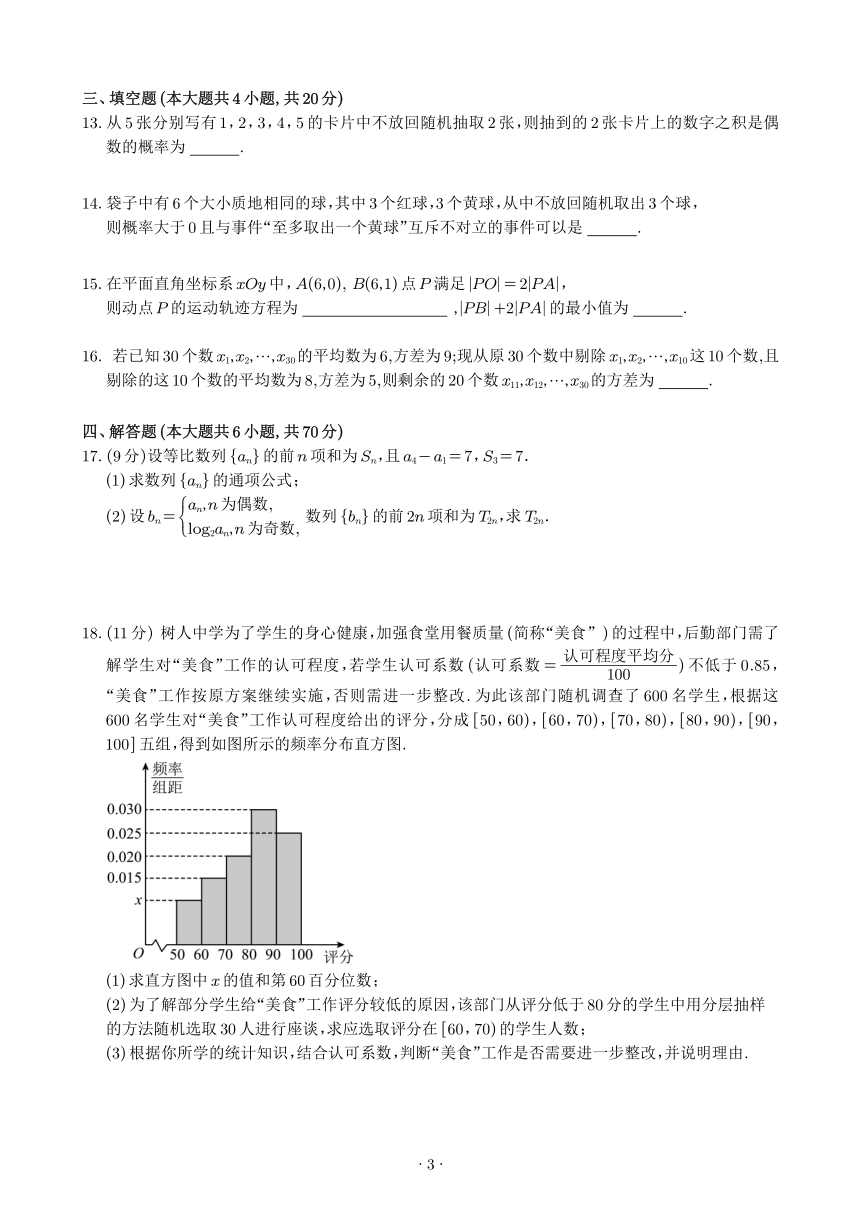
100]五组,得到如图所示的频率分布直方图.
(1)求直方图中 x的值和第 60百分位数;
(2)为了解部分学生给“美食”工作评分较低的原因,该部门从评分低于 80分的学生中用分层抽样
的方法随机选取 30人进行座谈,求应选取评分在 [60,70)的学生人数;
(3)根据你所学的统计知识,结合认可系数,判断“美食”工作是否需要进一步整改,并说明理由.
·3·
19. (11分)已知函数 f(x) = x3- 3ax- 1在 x=-1处取得极值.
(1)求实数 a的值;
(2)当 x∈ [-2,1]时,求函数 f(x)的值域.
20. (12 1分)在平面直角坐标系 xOy中,动点N到F(2,0)的距离与它到直线 l:x= 2 的距离之比为 2,
记N的轨迹为曲线C.
(1)求曲线C的方程;
(2)过F的直线交曲线C于A,B两点 (均位于 y轴右侧),F关于原点的对称点为M ,
求△ABM的面积的取值范围.
21. (12分)甲、乙、丙三人进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空
者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,
直至其中一人被淘汰,另一人最终获胜,比赛结束。已知在每场比赛中,甲胜乙和甲胜丙的概率均
2 1
为 3 ,乙胜丙的概率为 2 ,各场比赛的结果相互独立.经抽签,第一场比赛甲轮空.
(1)求前三场比赛结束后,丙被淘汰的概率;
(2)求只需四场比赛就决出冠军的概率.
2
22. (12 ) C x分 已知椭圆 :4 + y
2= 1,设过点A 1,0 的直线 l交椭圆C于M,N两点,交直线 x= 4于
点P,点E为直线 x= 1上不同于点A的任意一点.
(1)求 AM 的最小值;
(2)记直线EM,EN,EP的斜率分别为 k1,k2,k3,问是否存在
k1,k2,k3的某种排列 ki,ki,ki (其中 i1 2 3 1,i2,i3 = 1,2,3 ),使得
ki,ki,ki 成等差数列或等比数列?若存在,写出结论,并加以证1 2 3
明;若不存在,说明理由.
23. (3分卷面分)
·4·
莆田名校 2022- 2023学年高二期下学期期中考参考答案 (B卷)
1. D
两个元件均故障,则电路故障
2. A
在 a和 b两数之间插入n个数,使它们与 a,b组成等差数列,则这个数列共有n+ 2项,
设该数列的公差为 d,则 d= b- a = b- a .
n+ 2 - 1 n+ 1
3. B
在 20组随机数中含 {2,3,4,5,6,7,8,9}中的数至少 3个 (含 3个或 4个),共有 15组,即模拟结果中射击 4
15
次,至少击中 3次的频率为 20 = 0.75.
据此估计该运动员射击 4次,至少击中 3次的概率为 0.75. (另外,正难则反)
4. C
分为三种情况:第一次通过,第二次通过,第三次通过,结合相互独立事件概率乘法公式求解.
【详解】由题意知,小王最终通过面试的概率为P= 0.7+ 0.3× 0.7+ 0.3× 0.3× 0.7= 0.973.
故选:C.
5. B
双曲线的渐近线为 y=± 3x,所以∠BOF=∠COx= 60°,所以∠BOC= 60°
所以BC=FB= b= 3
y C
B
F O x
6. C
设BF1=m,则AF1= 2m,BF2= 5m,AF
y
2= 4m,a= 3m A
于是∠DAF2= 90°,
所以AF 2 +AF 2 21 2 =F1F2 ,即 (2m)2+ (4m) 2= (2c)2,得 c = 5m, F1
故 e= ca =
5 O F2 x
3 B
7. A
2= , = p设抛物线方程为 y 2px 则 f 2 , (可令 p= 2)
2tan θ
由 tanθ= 2 =-4 5,则 tan θ = 52 2 sin
θ = 5 2
1- tan2 θ 2 3
,cosθ= 3
2
p p θ 2p
所以 |AF| = = ,d= 2|AF|sin 2 = sin
θ 2 5
1- cos(π- θ ) 1+ cos θ 1+ cos θ 2
= 5 p
2 2 2
f = 5所以 4 ,d
p 2
思路 2.设抛物线方程为 y2= 2px(p> 0),F( ,0),y = d ( d2 A 2 2 )
2= 2px x= d8p
·5·
d
2 = tan θ = 5由 4 5p2p 2 2 2 - 8dp-
f p
5d2= 0 p= 52 d = =
5
- d d 2d 42 8p
8. C
如图抛掷两枚骰子,点数之和如下:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
则投掷出的点数和频数如下
点数和 2 3 4 5 6 7 8 9 10 11 12
频数 1 2 3 4 5 6 5 4 3 2 1
若n= 2,则如下图所示,游戏是公平的
点数和余数 0 1
频数 18 18
若n= 3则如下图所示,游戏是公平的
点数和余数 0 1 2
频数 12 12 12
若n= 4则如下图所示,游戏是不公平的
点数和余数 0 1 2 3
频数 9 8 9 10
若n= 6则如下图所示,游戏是公平的
点数和余数 0 1 2 3 4 5
频数 6 6 6 6 6 6
9. BCD
因为A,B是两个随机事件,
所以A+B表示两个事件至少有一个发生,故B正确;
AB+AB表示两个事件恰有一个发生,故A错误;
A+B表示两个事件均不发生,故C正确;
AB表示两个事件均不发生,故D正确.故选:BCD.
10. AB
选项A,乙同学体温的极差为 36.5- 36.3= 0.2℃,故A正确;
选项B,乙同学的体温从低到高依次为 36.3℃,36.3℃,36.4℃,36.4℃,36.4℃,36.5℃,36.5℃,故众数
为 36.4℃,而中位数和平均数都是 36.4℃,故B正确;
选项C,从折线图上可以看出,乙同学的体温比甲同学的体温稳定,故C错误;
选项D,甲同学的体温从低到高依次为 36.2℃,36.2℃,36.4℃,36.4℃,36.5℃,36.5℃,36.6℃,
由 70%× 7= 4.9,可知数据的第 70百分位数为第 5项数据 36.5℃,故D错误.
11. AC
由题可知,A=“x+ y= 7”,B=“xy奇数”,C=“x> 3”,
则事件A的所有情况为:(1,6),(2,5),(3,4),(4,3) (5,2) (6,1) 6 P(A) = 6 1, , 共 种情况,所以 6× 6 = 6 ;
事件B的所有情况为:(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5)共 9种情况,
·6·
所以P(B) = 9 16× 6 = 4 ,所以A与B互斥但不对立,故A正确;B错误;
事件C的所有情况为:(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 18 P(C) = 18 = 1, , , , , ,共 种情况, 6× 6 2
P(AC) = 3 = 1 P(A) P(C) = 1 × 1 = 16× 6 12 , 6 2 12 ,P(AC) =P(A) P(C),所以A与C独立,C正确.
P(BC) = 3 16× 6 = 12 ≠P(B)P(C),可知,D错误,
12. ACD
由抛物线的对称性,不妨设直线 l的方程为 y= k(x- 1),A(x1,y1),B(x2,y2)
y2= 4x
则由 λ> 1则 x1> x2由 = ( - )整理得 k
2x2+ (2k2- 4)x+ k2= 0
y k x 1
由Δ= 16- 16k2> 0且 k2≠ 0,由韦达定理得 x1x2= 1,
选项A.由上述不等式解得 k∈ (-1,0) ∪ (0,1),故A正确
M N
选项B.若 |BF| = x + 1= 3 , x 12 2 则 2= 2 ,x1= 2,|AF| = x1+ 1= 3,故B错误. B
选项C.|CB| = |BA|,设A,B在准线上的投影分别为A1,B1,
则 |BB1| = 12 |AA | |BF| =
1
1 即 2 |AF|故C正确.
|BM | = |CB| = |BBD. 1. 1| |BF|选项 思路 如图 | | | | | = △BFM △AFNAN CA AA1| |AF|
所以∠AFN= 60° |AF| = 2- ° = 41 cos60
思路 2.由抛物线几何平均性质可知,B关于 x轴的对称点B'与F,A三点共线,
所以∠BFM=∠B'FM=∠AFx=∠AFB ∠AFN= 60°,其余同上
∠ |CF| = |CB|思路 3.若BF平分 AFC,则由角平分线定理可得 |AF| |AB|,
|CF| |CB| |CB| |BB1| |BF|
所以 |AF| +|CF| = | | +| | =AB CB | = =AC| |AA1| |AF|
2 = x2+ 1即 x + 3 x + 1 化简得 3x2- x1+ 2= 0
3
,所以 x - x1+ 2= 0解得 x1= 3,故选项D正确。1 1 1
思路 4.只需∠AFC= 2∠BFC即 tan∠AFC= tan2∠BFC,所以有
y1 = 2y2(x2- 1) k(x1+ 1) = 2k(x2+ 1) (x2- 1) (x1+ x1x2) 2(x2+ 1) (x2- 1)x - 1 (x - 1)2- y21 2 2 x - 1 (x - 1)2 2
=
1 2 - y2 x1- x1x2 (x2- 1)2- y22
即-2(x2- 1)2= (x - 1)2- y22 2= (x - 1)2- 4x 即 3x22 2 2- 10x2+ 3= 0 x = 1解得 2 3 或 3(舍去)
13. 710
从 5张卡片中无放回抽取 2张,共有 1,2 , 1,3 , 1,4 , 1,5 , 2,3 , 2,4 , 2,5 , 3,4 , 3,5 , 4,5 这 10
3 7
种情况,其中数字之积为奇数的有 1,3 , 1,5 , 3,5 共 3种情况,故所求概率为 1- 10 = 10 .
14. 取出 2个黄球和 1个红球; 取出 3个黄球
事件“至多取出一个黄球”的对立事件为“至少取出 2个黄球”
15.
答案:(x- 8)2+ y2= 16, 37
解析:由阿波罗尼斯圆性质知:点P在圆 (x- 8)2+ y2= 16上,
|PB| +2|PA| = |PB| +|PM | ≥ |BM | = 37
16. 8
: 依题意 z= 6,S2z= ,
9 x= 8,S 2x= 5,
由 z= 13 x+
2
3 y得 y= 5
·7·
由S2z= 1 2
3 (Sx+ (x- z)
2) + 2 23 (Sy+ (
y- z)2) = 9 S2y= 8
a1q
3- a1= 7, ①
17. 则有 a1(1- q3) 2分1- q = 7, ②
由①÷②得 q- 1= 1,所以 q= 2,代入①得 a1= 1,所以 a = 2n-1n ; 4分
2n-1,n为偶数,
(2)由 (1)可得 bn= 5分n- 1,n为奇数,
所以T2n= b1+ b2+ +b2n= (b1+ b3+ +b2n-1) + (b2+ b4+ +b2n)
= (0+ 2+ 4+ +2n- 2) + (2+ 23+ +22n-1) 6分
= (2n- 2)n
n
2 +
2(1- 4 )
1- 4 8分
= 13 2
2n+1+n2-n- 23 . 9分
18. (1)由图可知:10× (x+ 0.015+ 0.02+ 0.03+ 0.025) = 1,∴ x= 0.01, 3分
0.6- 0.1+ 0.15+ 0.2
60百分位数:80+ 0.03 = 80+
15
3 = 85; 5分
(2)低于 80分的学生中三组学生的人数比例为 0.1:0.15:0.2= 2:3:4,
3
则应选取评分在 60,70 的学生人数为:30× 2+ 3+ 4 = 10(人) 8分
(3)由图可知,认可程度平均分为:
x = 55× 0.1+ 65× 0.15+ 75× 0.2+ 85× 0.3+ 95× 0.25= 79.5< 0.85× 100= 85, 10分
∴“美食”工作需要进一步整改. 11分
19. 解:(1) ∵ f(x) = x3- 3ax- 1在 x=-1处取得极值,且 f′ x = 3x2- 3a,
∴ f′ (-1) = 3× (-1)2- 3a= 0,
∴ a= 1,经验证符合题意; 4分
(2)由 (1)得 f(x) = x3- 3x- 1,f′ (x) = 3x2- 3,
∴由 f′ (x) = 0解得 x1=-1,x2= 1,
当 x∈ [-2,-1)时,f′ (x)> 0,当 x∈ (-1,1]时,f′ (x)≤ 0,
∴ f(x)在 [-2,-1)上单调递增,在 (-1,1]上单调递减,
∴当 x=-1时,函数取得最大值 f(-1) = 1,
又 f(-2) =-3,f(1) =-3,
∴函数 f(x)在 [-2,1]上的值域是 [-3,1]. 11分
(x- 2)2+ y2
20. (1)设点N (x,y),依题意有 1 = 2|x- 2 |
2
即 (x- 2)2+ y2= (2x- 1)2, y化简得 x2- 3 = 1 4分
2
(2) y由题意,直线 l的斜率不为 0,设直线 l的方程为 x=my+ 2,代入 x2- 3 = 1,
整理可得:(3m2- 1)y2+ 12my+ 9= 0,设A(x1,y1),B(x2,y2),
-12m 9
则 y1+ y 22= 2 ,y1y2= 2 < 0,所以 3m - 1< 0,△= 36(m
2+ 1)
3m - 1 3m - 1
2 2
∴ |y - y | = 6 m + 1 11 2 ( 2- )2 ,∴S△ABF= 2 × 2c× |y1- y | = 12
m + 1 ,
3m 1 1 2 (3m2- 1)2
1
设 3m2- 1= t,则-1≤ t< 0,t ≤-1,
∴S t+ 4△ABF= 12 2 = 12
1 ( 43 2 +
1
t ) = 12
4 1 1 2 1
1 3t t 3
( t + 8 ) - 48 ≥ 12,
·8·
1
当 t =-1时,取等号,所以△ABM的面积的取值范围是 12,+∞ . 12分
21. 【分析】(1)前三场比赛结束后,丙被淘汰的情况有 2种①乙胜丙、乙胜甲、乙胜丙②乙胜丙、甲胜乙、甲
胜丙,再利用相互独立事件概率的乘法运算即可得出答案.
(2)首先分析出只需四场比赛就决出冠军的情况,再利用相互独立事件概率的乘法运算即可得出答案.
(3)首先分析出甲最终获胜的情况,再利用相互独立事件概率的乘法运算即可得出答案.
2 (1) A P A = P A = 1【详解】 记事件 为甲胜乙,则 3 , 3 ,
事件B为甲胜丙,则P B = 2 3 ,P B =
1
3 ,
事件C 1 1为乙胜丙,则P C = 2 ,P C = 2 ,
前三场比赛结束后,丙被淘汰的概率为
P1=P CAC +P CAB = 1 × 1 × 1 + 1 × 2 × 2 = 11 2 3 2 2 3 3 36 6分
(2)只需四场比赛就决出冠军的概率为
P2=P CACA +P CBCB +P CABA +P CBAB
= 1 1 12 × 3 × 2 ×
1 1 1 1 1 1 2 2 2 1 2 2 2
3 + 2 × 3 × 2 × 3 + 2 × 3 × 3 × 3 + 2 × 3 × 3 × 3 =
19
54. 12分
根据“累计负两场者被淘汰”列表如下:
第一场负方 第二场负方 第三场负方 第四场负方 第五场负方 最终获胜者
甲 丙
乙 丙 甲 丙丙 甲
甲 甲 乙 丙丙 乙
丙
乙 甲 丙
乙 丙 甲丙 甲
乙 甲 甲 丙丙 甲
丙 丙 甲 乙
甲 乙 甲
乙 甲 丙丙 甲
丙
22. (1)
2
设点M x,y x ,其中 24 + y = 1,
2
则 |AM | = (x- 1)2+ y2= (x- 1)2+ 1- x = 34 4 x
2- 2x+ 2,x∈ [-2,2]
= 34 (x
2- 83 x) +
2 6 4 6
3 ≥ 3 ,当 x= 3 时取最小值 3 4分
(2)k1,k3,k2或 k2,k3,k1成等差数列,证明如下: 5分
C: x
2
则 + y24 = 1,设点E 1,t ,t≠ 0.
①若直线 l斜率为 0,则点P 4,0 ,不妨令点M 2,0 ,N -2,0 ,
则 k1=-t,k = t2 3 ,k3=-
t
3 ,此时 k1,k2,k3的任意排列 ki1,ki2,ki3均不成等比数列,
k1,k3,k2或 k2,k3,k1成等差数列. 6分
②直线 l斜率不为 0,设直线 l:x=my+ 1(m≠ 0),M (x1,y1)N (x2,y2),
则点P 4, 3m ,
·9·
x=my+ 1由 x2 + 2= 得 (m2+ 4)y2+ 2my- 3= 0,Δ= 16(m2+ 3)> 0,4 y 1
故 y + y -2m -31 2= 2 ,ym + 4 1
y2= 2 ,m + 4
3
y - t y - t
k = 1 ,k = 2- t ,k = m = 3-mt因为 1 x 21- 1 x 32- 1 3 3m
,
y1- t y2- t y1- t y2- t
所以 k1+ k2= x +1- 1 x2- 1
= my +1 my2
= y2(y1- t) + y1(y2- t) = 2y1y2- t(y1+ y2)my1y2 my1y2
-6 2mt
m2= +
+
4 m2+ 4 = 6- 2mt-3m 3m = 2k3,
m2+ 4
所以 k1,k3,k2或 k2,k3,k1成等差数列,
综合上述,k1,k3,k2或 k2,k3,k1成等差数列. 12分
·10·
数 学 试 题
本试卷共 4页 全卷满分 150分 考试用时 120分钟
一、单选题 (本大题共 8小题,共 40分)
1.甲、乙两个元件构成一并联电路,设E=“甲元件故障”,F=“乙元件故障”,则表示电路故障的事件
为 ( )
A. E∪F B. E∪F C. E∩F D. E∩F
2.在 a和 b两数之间插入n个数,使它们与 a,b组成等差数列,则该数列的公差为 ( )
A. b- an+ 1 B.
b- a C. b- an n+ 2 D.
a- b
n+ 2
3.已知某运动员每次射击击中目标的概率为 80%.现采用随机模拟的方法估计某运动员射击 4次,至
少击中 3次的概率.先由计算器给出 0到 9之间取整数值的随机数,指定 0,1表示没有击中目标,
2,3,4,5,6,7,8,9表示击中目标,以 4个随机数为一组,代表射击 4次的结果,经随机模拟产生
了 20组随机数:
7527 0293 7140 9857 0347 4373 8636
6947 7610 4281 1417 4698 0371 6233
2616 8045 6011 3661 9597 7424
根据以上数据估计该射击运动员射击 4次,至少击中 3次的概率为 ( )
A. 0.8 B. 0.75 C. 0.7 D. 0.65
4.某单位入职面试中有三道题目,有三次答题机会,一旦某次答对抽到的题目,则面试通过,否则就一
直抽题到第 3次为止.若求职者小王答对每道题目的概率都是 0.7,则他最终通过面试的概率为
( )
A. 0.7 B. 0.91 C. 0.973 D. 0.981
y2
5.已知双曲线E:x2- 3 = 1的左焦点为F,过点F作双曲线E的一条渐近线的垂线(垂足为B)交另
一条渐近线于点C,则线段BC的长度为 ( )
A. 1 B. 3 C. 2 D. 2 3
2 y2
6.设F1,F2分别为椭圆C: x2 + 2 = 1(a> b> 0)的左、右焦点,点A,B在C上,若F1A= 2BF1,2|F2B|a b
= 5|F1A|,则椭圆C的离心率为 ( )
A. 2 62 B. 4 C.
5 D. 103 5
·1·
7.图 1所示,抛物面天线是指由抛物面 (抛物线绕其对称轴旋转形成的曲面)反射器和位于焦点上的
照射器 (馈源,通常采用喇叭天线)组成的单反射面型天线,广泛应用于微波和卫星通讯等领域,具
有结构简单、方向性强、工作频带宽等特点.图 2是图
1的轴截面,A,B两点关于抛物线的对称轴对称,F是
抛物线的焦点,∠AFB是馈源的方向角,记为 θ,焦点F
f
到顶点的距离 f与口径 d的比值 称为抛物面天线的
d
焦径比,它直接影响天线的效率与信噪比等.如果某抛
物面天线馈源的方向角 θ满足 tanθ=-4 5,则其焦径
图 1 图 2
比为 ( )
A. 5 10 10 54 B. 4 C. 8 D. 8
8.在编号分别为 (i= 0,1,2,…,n- 1)的 n名同学中挑选一人参加某项活动,挑选方法如下:抛掷两枚
骰子,将两枚骰子的点数之和除以 n所得的余数如果恰好为 i,则选编号为 i的同学.下列哪种情况
是不 公 平 的挑选方法 ( )
A. n= 2 B. n= 3 C. n= 4 D. n= 6
二、多选题 (本大题共 4小题,共 20分,每道题全部选对的得 5分,部分选对得 2分,有选错得 0分.)
9.设A,B是两个随机事件,则下列说法正确的有 ( )
A. AB+AB表示两个事件至少有一个发生 B. A+B表示两个事件至少有一个发生
C. A+B表示两个事件均不发生 D. A B表示两个事件均不发生
10.某班级体温检测员对一周内甲 乙两名同学的体温进行了统计,其结果如图所示,则下列说法正确
的有 ( )
A. 乙同学体温的极差为 0.2℃
B. 乙同学体温的众数为 36.4℃,中位数与平均数相等
C. 甲同学的体温比乙同学的体温稳定
D. 甲同学体温的第 70百分位数为 36.6℃
11.抛掷一红一绿两枚质地均匀的骰子,记下骰子朝上面的点数.用 x表示红色骰子的点数,用 y表示绿
色骰子的点数,用 (x,y)表示一次试验的结果.定义事件:A=“x+ y= 7”,事件B=“xy为奇数”,
事件C=“x> 3”,则下列结论正确的有 ( )
A. A与B互斥但不对立 B. A与B对立
C. A与C相互独立 D. B与C相互独立
12.已知抛物线 E:y2= 4x的焦点为 F,准线交 x 轴于点 C ,直线 l 过 C 且交 E 于不同的A,B 两
点,且CA= λCB(λ> 1),下列命题正确的有 ( )
A. 直线 l的斜率 k∈ (-1,0) ∪ (0,1) B. 3若 |BF| = 2 ,则 |AF| = 4
C. 若 λ= 2,则 |AF| = 2|BF| D. 存在 λ使得BF平分∠AFC
·2·
三、填空题 (本大题共 4小题,共 20分)
13.从 5张分别写有 1,2,3,4,5的卡片中不放回随机抽取 2张,则抽到的 2张卡片上的数字之积是偶
数的概率为 .
14.袋子中有 6个大小质地相同的球,其中 3个红球,3个黄球,从中不放回随机取出 3个球,
则概率大于 0且与事件“至多取出一个黄球”互斥不对立的事件可以是 .
15.在平面直角坐标系 xOy中,A(6,0), B(6,1)点P满足 |PO| = 2|PA|,
则动点P的运动轨迹方程为 ,|PB| +2|PA|的最小值为 .
16. 若已知 30个数 x1,x2, ,x30的平均数为 6,方差为 9;现从原 30个数中剔除 x1,x2, ,x10这 10个数,且
剔除的这 10个数的平均数为 8,方差为 5,则剩余的 20个数 x11,x12, ,x30的方差为 .
四、解答题 (本大题共 6小题,共 70分)
17. (9分)设等比数列 {an}的前n项和为Sn,且 a4- a1= 7,S3= 7.
(1)求数列 {an}的通项公式;
an,n为偶数,(2)设 bn= 数列 {bn}的前 2n项和为T, 2n,求T2n.log2an n为奇数,
18. (11分) 树人中学为了学生的身心健康,加强食堂用餐质量 (简称“美食”)的过程中,后勤部门需了
认可程度平均分
解学生对“美食”工作的认可程度,若学生认可系数 (认可系数= 100 )不低于 0.85,
“美食”工作按原方案继续实施,否则需进一步整改. 为此该部门随机调查了 600 名学生,根据这
600名学生对“美食”工作认可程度给出的评分,分成 [50,60),[60,70),[70,80),[80,90),[90,
100]五组,得到如图所示的频率分布直方图.
(1)求直方图中 x的值和第 60百分位数;
(2)为了解部分学生给“美食”工作评分较低的原因,该部门从评分低于 80分的学生中用分层抽样
的方法随机选取 30人进行座谈,求应选取评分在 [60,70)的学生人数;
(3)根据你所学的统计知识,结合认可系数,判断“美食”工作是否需要进一步整改,并说明理由.
·3·
19. (11分)已知函数 f(x) = x3- 3ax- 1在 x=-1处取得极值.
(1)求实数 a的值;
(2)当 x∈ [-2,1]时,求函数 f(x)的值域.
20. (12 1分)在平面直角坐标系 xOy中,动点N到F(2,0)的距离与它到直线 l:x= 2 的距离之比为 2,
记N的轨迹为曲线C.
(1)求曲线C的方程;
(2)过F的直线交曲线C于A,B两点 (均位于 y轴右侧),F关于原点的对称点为M ,
求△ABM的面积的取值范围.
21. (12分)甲、乙、丙三人进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空
者进行下一场比赛,负者下一场轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,
直至其中一人被淘汰,另一人最终获胜,比赛结束。已知在每场比赛中,甲胜乙和甲胜丙的概率均
2 1
为 3 ,乙胜丙的概率为 2 ,各场比赛的结果相互独立.经抽签,第一场比赛甲轮空.
(1)求前三场比赛结束后,丙被淘汰的概率;
(2)求只需四场比赛就决出冠军的概率.
2
22. (12 ) C x分 已知椭圆 :4 + y
2= 1,设过点A 1,0 的直线 l交椭圆C于M,N两点,交直线 x= 4于
点P,点E为直线 x= 1上不同于点A的任意一点.
(1)求 AM 的最小值;
(2)记直线EM,EN,EP的斜率分别为 k1,k2,k3,问是否存在
k1,k2,k3的某种排列 ki,ki,ki (其中 i1 2 3 1,i2,i3 = 1,2,3 ),使得
ki,ki,ki 成等差数列或等比数列?若存在,写出结论,并加以证1 2 3
明;若不存在,说明理由.
23. (3分卷面分)
·4·
莆田名校 2022- 2023学年高二期下学期期中考参考答案 (B卷)
1. D
两个元件均故障,则电路故障
2. A
在 a和 b两数之间插入n个数,使它们与 a,b组成等差数列,则这个数列共有n+ 2项,
设该数列的公差为 d,则 d= b- a = b- a .
n+ 2 - 1 n+ 1
3. B
在 20组随机数中含 {2,3,4,5,6,7,8,9}中的数至少 3个 (含 3个或 4个),共有 15组,即模拟结果中射击 4
15
次,至少击中 3次的频率为 20 = 0.75.
据此估计该运动员射击 4次,至少击中 3次的概率为 0.75. (另外,正难则反)
4. C
分为三种情况:第一次通过,第二次通过,第三次通过,结合相互独立事件概率乘法公式求解.
【详解】由题意知,小王最终通过面试的概率为P= 0.7+ 0.3× 0.7+ 0.3× 0.3× 0.7= 0.973.
故选:C.
5. B
双曲线的渐近线为 y=± 3x,所以∠BOF=∠COx= 60°,所以∠BOC= 60°
所以BC=FB= b= 3
y C
B
F O x
6. C
设BF1=m,则AF1= 2m,BF2= 5m,AF
y
2= 4m,a= 3m A
于是∠DAF2= 90°,
所以AF 2 +AF 2 21 2 =F1F2 ,即 (2m)2+ (4m) 2= (2c)2,得 c = 5m, F1
故 e= ca =
5 O F2 x
3 B
7. A
2= , = p设抛物线方程为 y 2px 则 f 2 , (可令 p= 2)
2tan θ
由 tanθ= 2 =-4 5,则 tan θ = 52 2 sin
θ = 5 2
1- tan2 θ 2 3
,cosθ= 3
2
p p θ 2p
所以 |AF| = = ,d= 2|AF|sin 2 = sin
θ 2 5
1- cos(π- θ ) 1+ cos θ 1+ cos θ 2
= 5 p
2 2 2
f = 5所以 4 ,d
p 2
思路 2.设抛物线方程为 y2= 2px(p> 0),F( ,0),y = d ( d2 A 2 2 )
2= 2px x= d8p
·5·
d
2 = tan θ = 5由 4 5p2p 2 2 2 - 8dp-
f p
5d2= 0 p= 52 d = =
5
- d d 2d 42 8p
8. C
如图抛掷两枚骰子,点数之和如下:
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
则投掷出的点数和频数如下
点数和 2 3 4 5 6 7 8 9 10 11 12
频数 1 2 3 4 5 6 5 4 3 2 1
若n= 2,则如下图所示,游戏是公平的
点数和余数 0 1
频数 18 18
若n= 3则如下图所示,游戏是公平的
点数和余数 0 1 2
频数 12 12 12
若n= 4则如下图所示,游戏是不公平的
点数和余数 0 1 2 3
频数 9 8 9 10
若n= 6则如下图所示,游戏是公平的
点数和余数 0 1 2 3 4 5
频数 6 6 6 6 6 6
9. BCD
因为A,B是两个随机事件,
所以A+B表示两个事件至少有一个发生,故B正确;
AB+AB表示两个事件恰有一个发生,故A错误;
A+B表示两个事件均不发生,故C正确;
AB表示两个事件均不发生,故D正确.故选:BCD.
10. AB
选项A,乙同学体温的极差为 36.5- 36.3= 0.2℃,故A正确;
选项B,乙同学的体温从低到高依次为 36.3℃,36.3℃,36.4℃,36.4℃,36.4℃,36.5℃,36.5℃,故众数
为 36.4℃,而中位数和平均数都是 36.4℃,故B正确;
选项C,从折线图上可以看出,乙同学的体温比甲同学的体温稳定,故C错误;
选项D,甲同学的体温从低到高依次为 36.2℃,36.2℃,36.4℃,36.4℃,36.5℃,36.5℃,36.6℃,
由 70%× 7= 4.9,可知数据的第 70百分位数为第 5项数据 36.5℃,故D错误.
11. AC
由题可知,A=“x+ y= 7”,B=“xy奇数”,C=“x> 3”,
则事件A的所有情况为:(1,6),(2,5),(3,4),(4,3) (5,2) (6,1) 6 P(A) = 6 1, , 共 种情况,所以 6× 6 = 6 ;
事件B的所有情况为:(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5)共 9种情况,
·6·
所以P(B) = 9 16× 6 = 4 ,所以A与B互斥但不对立,故A正确;B错误;
事件C的所有情况为:(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) 18 P(C) = 18 = 1, , , , , ,共 种情况, 6× 6 2
P(AC) = 3 = 1 P(A) P(C) = 1 × 1 = 16× 6 12 , 6 2 12 ,P(AC) =P(A) P(C),所以A与C独立,C正确.
P(BC) = 3 16× 6 = 12 ≠P(B)P(C),可知,D错误,
12. ACD
由抛物线的对称性,不妨设直线 l的方程为 y= k(x- 1),A(x1,y1),B(x2,y2)
y2= 4x
则由 λ> 1则 x1> x2由 = ( - )整理得 k
2x2+ (2k2- 4)x+ k2= 0
y k x 1
由Δ= 16- 16k2> 0且 k2≠ 0,由韦达定理得 x1x2= 1,
选项A.由上述不等式解得 k∈ (-1,0) ∪ (0,1),故A正确
M N
选项B.若 |BF| = x + 1= 3 , x 12 2 则 2= 2 ,x1= 2,|AF| = x1+ 1= 3,故B错误. B
选项C.|CB| = |BA|,设A,B在准线上的投影分别为A1,B1,
则 |BB1| = 12 |AA | |BF| =
1
1 即 2 |AF|故C正确.
|BM | = |CB| = |BBD. 1. 1| |BF|选项 思路 如图 | | | | | = △BFM △AFNAN CA AA1| |AF|
所以∠AFN= 60° |AF| = 2- ° = 41 cos60
思路 2.由抛物线几何平均性质可知,B关于 x轴的对称点B'与F,A三点共线,
所以∠BFM=∠B'FM=∠AFx=∠AFB ∠AFN= 60°,其余同上
∠ |CF| = |CB|思路 3.若BF平分 AFC,则由角平分线定理可得 |AF| |AB|,
|CF| |CB| |CB| |BB1| |BF|
所以 |AF| +|CF| = | | +| | =AB CB | = =AC| |AA1| |AF|
2 = x2+ 1即 x + 3 x + 1 化简得 3x2- x1+ 2= 0
3
,所以 x - x1+ 2= 0解得 x1= 3,故选项D正确。1 1 1
思路 4.只需∠AFC= 2∠BFC即 tan∠AFC= tan2∠BFC,所以有
y1 = 2y2(x2- 1) k(x1+ 1) = 2k(x2+ 1) (x2- 1) (x1+ x1x2) 2(x2+ 1) (x2- 1)x - 1 (x - 1)2- y21 2 2 x - 1 (x - 1)2 2
=
1 2 - y2 x1- x1x2 (x2- 1)2- y22
即-2(x2- 1)2= (x - 1)2- y22 2= (x - 1)2- 4x 即 3x22 2 2- 10x2+ 3= 0 x = 1解得 2 3 或 3(舍去)
13. 710
从 5张卡片中无放回抽取 2张,共有 1,2 , 1,3 , 1,4 , 1,5 , 2,3 , 2,4 , 2,5 , 3,4 , 3,5 , 4,5 这 10
3 7
种情况,其中数字之积为奇数的有 1,3 , 1,5 , 3,5 共 3种情况,故所求概率为 1- 10 = 10 .
14. 取出 2个黄球和 1个红球; 取出 3个黄球
事件“至多取出一个黄球”的对立事件为“至少取出 2个黄球”
15.
答案:(x- 8)2+ y2= 16, 37
解析:由阿波罗尼斯圆性质知:点P在圆 (x- 8)2+ y2= 16上,
|PB| +2|PA| = |PB| +|PM | ≥ |BM | = 37
16. 8
: 依题意 z= 6,S2z= ,
9 x= 8,S 2x= 5,
由 z= 13 x+
2
3 y得 y= 5
·7·
由S2z= 1 2
3 (Sx+ (x- z)
2) + 2 23 (Sy+ (
y- z)2) = 9 S2y= 8
a1q
3- a1= 7, ①
17. 则有 a1(1- q3) 2分1- q = 7, ②
由①÷②得 q- 1= 1,所以 q= 2,代入①得 a1= 1,所以 a = 2n-1n ; 4分
2n-1,n为偶数,
(2)由 (1)可得 bn= 5分n- 1,n为奇数,
所以T2n= b1+ b2+ +b2n= (b1+ b3+ +b2n-1) + (b2+ b4+ +b2n)
= (0+ 2+ 4+ +2n- 2) + (2+ 23+ +22n-1) 6分
= (2n- 2)n
n
2 +
2(1- 4 )
1- 4 8分
= 13 2
2n+1+n2-n- 23 . 9分
18. (1)由图可知:10× (x+ 0.015+ 0.02+ 0.03+ 0.025) = 1,∴ x= 0.01, 3分
0.6- 0.1+ 0.15+ 0.2
60百分位数:80+ 0.03 = 80+
15
3 = 85; 5分
(2)低于 80分的学生中三组学生的人数比例为 0.1:0.15:0.2= 2:3:4,
3
则应选取评分在 60,70 的学生人数为:30× 2+ 3+ 4 = 10(人) 8分
(3)由图可知,认可程度平均分为:
x = 55× 0.1+ 65× 0.15+ 75× 0.2+ 85× 0.3+ 95× 0.25= 79.5< 0.85× 100= 85, 10分
∴“美食”工作需要进一步整改. 11分
19. 解:(1) ∵ f(x) = x3- 3ax- 1在 x=-1处取得极值,且 f′ x = 3x2- 3a,
∴ f′ (-1) = 3× (-1)2- 3a= 0,
∴ a= 1,经验证符合题意; 4分
(2)由 (1)得 f(x) = x3- 3x- 1,f′ (x) = 3x2- 3,
∴由 f′ (x) = 0解得 x1=-1,x2= 1,
当 x∈ [-2,-1)时,f′ (x)> 0,当 x∈ (-1,1]时,f′ (x)≤ 0,
∴ f(x)在 [-2,-1)上单调递增,在 (-1,1]上单调递减,
∴当 x=-1时,函数取得最大值 f(-1) = 1,
又 f(-2) =-3,f(1) =-3,
∴函数 f(x)在 [-2,1]上的值域是 [-3,1]. 11分
(x- 2)2+ y2
20. (1)设点N (x,y),依题意有 1 = 2|x- 2 |
2
即 (x- 2)2+ y2= (2x- 1)2, y化简得 x2- 3 = 1 4分
2
(2) y由题意,直线 l的斜率不为 0,设直线 l的方程为 x=my+ 2,代入 x2- 3 = 1,
整理可得:(3m2- 1)y2+ 12my+ 9= 0,设A(x1,y1),B(x2,y2),
-12m 9
则 y1+ y 22= 2 ,y1y2= 2 < 0,所以 3m - 1< 0,△= 36(m
2+ 1)
3m - 1 3m - 1
2 2
∴ |y - y | = 6 m + 1 11 2 ( 2- )2 ,∴S△ABF= 2 × 2c× |y1- y | = 12
m + 1 ,
3m 1 1 2 (3m2- 1)2
1
设 3m2- 1= t,则-1≤ t< 0,t ≤-1,
∴S t+ 4△ABF= 12 2 = 12
1 ( 43 2 +
1
t ) = 12
4 1 1 2 1
1 3t t 3
( t + 8 ) - 48 ≥ 12,
·8·
1
当 t =-1时,取等号,所以△ABM的面积的取值范围是 12,+∞ . 12分
21. 【分析】(1)前三场比赛结束后,丙被淘汰的情况有 2种①乙胜丙、乙胜甲、乙胜丙②乙胜丙、甲胜乙、甲
胜丙,再利用相互独立事件概率的乘法运算即可得出答案.
(2)首先分析出只需四场比赛就决出冠军的情况,再利用相互独立事件概率的乘法运算即可得出答案.
(3)首先分析出甲最终获胜的情况,再利用相互独立事件概率的乘法运算即可得出答案.
2 (1) A P A = P A = 1【详解】 记事件 为甲胜乙,则 3 , 3 ,
事件B为甲胜丙,则P B = 2 3 ,P B =
1
3 ,
事件C 1 1为乙胜丙,则P C = 2 ,P C = 2 ,
前三场比赛结束后,丙被淘汰的概率为
P1=P CAC +P CAB = 1 × 1 × 1 + 1 × 2 × 2 = 11 2 3 2 2 3 3 36 6分
(2)只需四场比赛就决出冠军的概率为
P2=P CACA +P CBCB +P CABA +P CBAB
= 1 1 12 × 3 × 2 ×
1 1 1 1 1 1 2 2 2 1 2 2 2
3 + 2 × 3 × 2 × 3 + 2 × 3 × 3 × 3 + 2 × 3 × 3 × 3 =
19
54. 12分
根据“累计负两场者被淘汰”列表如下:
第一场负方 第二场负方 第三场负方 第四场负方 第五场负方 最终获胜者
甲 丙
乙 丙 甲 丙丙 甲
甲 甲 乙 丙丙 乙
丙
乙 甲 丙
乙 丙 甲丙 甲
乙 甲 甲 丙丙 甲
丙 丙 甲 乙
甲 乙 甲
乙 甲 丙丙 甲
丙
22. (1)
2
设点M x,y x ,其中 24 + y = 1,
2
则 |AM | = (x- 1)2+ y2= (x- 1)2+ 1- x = 34 4 x
2- 2x+ 2,x∈ [-2,2]
= 34 (x
2- 83 x) +
2 6 4 6
3 ≥ 3 ,当 x= 3 时取最小值 3 4分
(2)k1,k3,k2或 k2,k3,k1成等差数列,证明如下: 5分
C: x
2
则 + y24 = 1,设点E 1,t ,t≠ 0.
①若直线 l斜率为 0,则点P 4,0 ,不妨令点M 2,0 ,N -2,0 ,
则 k1=-t,k = t2 3 ,k3=-
t
3 ,此时 k1,k2,k3的任意排列 ki1,ki2,ki3均不成等比数列,
k1,k3,k2或 k2,k3,k1成等差数列. 6分
②直线 l斜率不为 0,设直线 l:x=my+ 1(m≠ 0),M (x1,y1)N (x2,y2),
则点P 4, 3m ,
·9·
x=my+ 1由 x2 + 2= 得 (m2+ 4)y2+ 2my- 3= 0,Δ= 16(m2+ 3)> 0,4 y 1
故 y + y -2m -31 2= 2 ,ym + 4 1
y2= 2 ,m + 4
3
y - t y - t
k = 1 ,k = 2- t ,k = m = 3-mt因为 1 x 21- 1 x 32- 1 3 3m
,
y1- t y2- t y1- t y2- t
所以 k1+ k2= x +1- 1 x2- 1
= my +1 my2
= y2(y1- t) + y1(y2- t) = 2y1y2- t(y1+ y2)my1y2 my1y2
-6 2mt
m2= +
+
4 m2+ 4 = 6- 2mt-3m 3m = 2k3,
m2+ 4
所以 k1,k3,k2或 k2,k3,k1成等差数列,
综合上述,k1,k3,k2或 k2,k3,k1成等差数列. 12分
·10·
同课章节目录
