2022-2023学年人教版数学八年级下册18.1探索平行四边形的性质课件(共34张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学八年级下册18.1探索平行四边形的性质课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 832.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 10:28:06 | ||
图片预览







文档简介
(共34张PPT)
·初二数学单元主题教学
探索平行四边形及
特殊的平行四边形的性质
一
探索平行四边形的性质
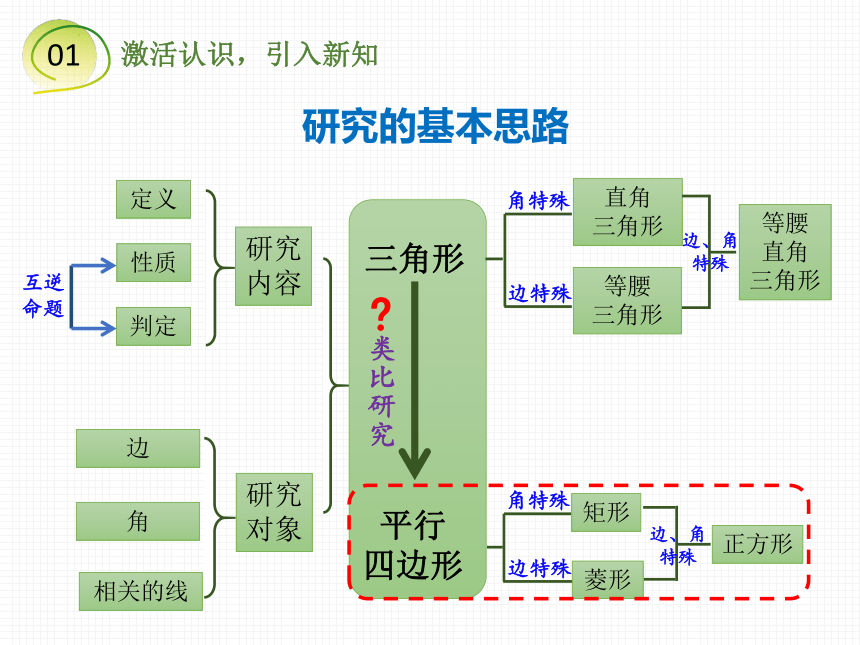
研究的基本思路
01
激活认识,引入新知
研究的基本思路
01
激活认识,引入新知
三角形
类比研究
直角
三角形
等腰
三角形
等腰
直角
三角形
矩形
菱形
正方形
研究内容
研究对象
定义
性质
判定
边
角
相关的线
互逆命题
角特殊
边特殊
角特殊
边特殊
平行
四边形
边、角
特殊
边、角
特殊
A
B
C
D
平行四边形用“ ”表示,如图,
平行四边形ABCD记作“ ABCD”.
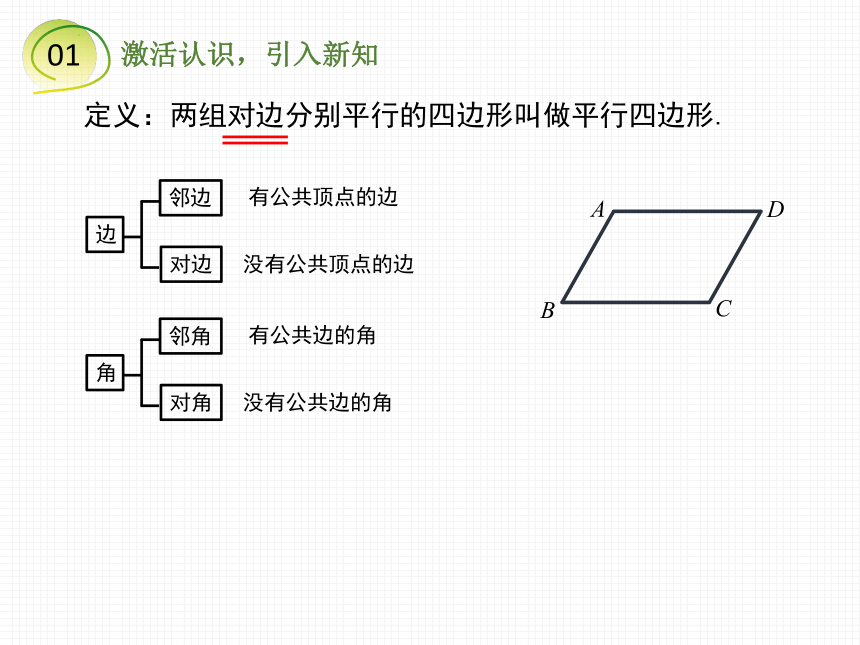
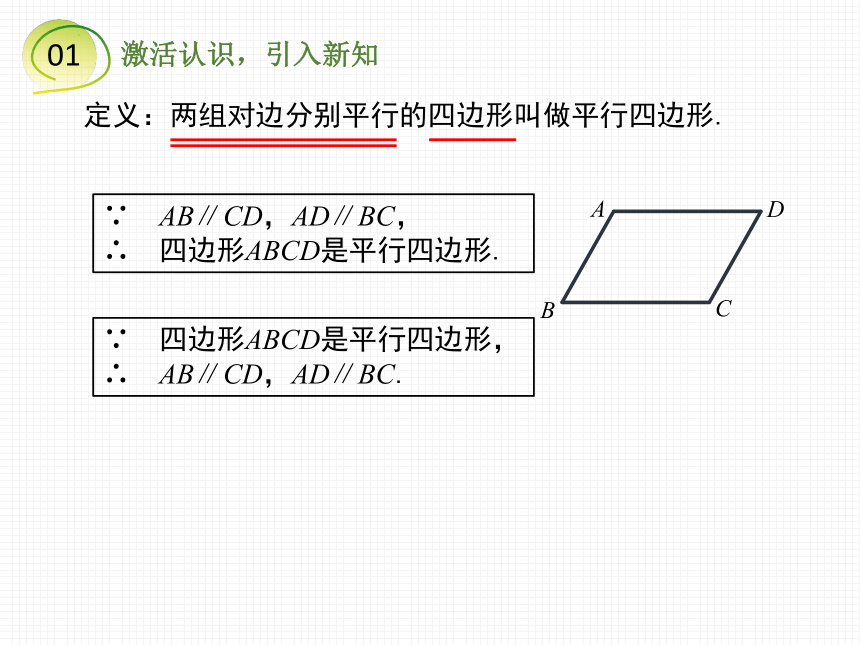
定义:两组对边分别平行的四边形叫做平行四边形.
01
激活认识,引入新知
边
对边
邻边
有公共顶点的边
没有公共顶点的边
定义:两组对边分别平行的四边形叫做平行四边形.
角
对角
邻角
有公共边的角
没有公共边的角
A
B
C
D
01
激活认识,引入新知
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
01
激活认识,引入新知
【活动1】 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,还可能具有哪些性质?度量一下,和你的猜想一致吗?
平行四边形
的性质
边
角
研究 对象
线
基本
元素
相关元素
活动要求:
(1)独立观察思考,写出猜想;
(2)小组交流,完善猜想;
(3)小组派代表进行班级交流展示.
02
经验迁移,提出猜想
对边
AB∥CD,AD∥BC AB=CD,AD=BC
邻角
∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°,∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
发现:
对角线
OA=OC,OB=OD
A
B
C
D
O
02
经验迁移,提出猜想
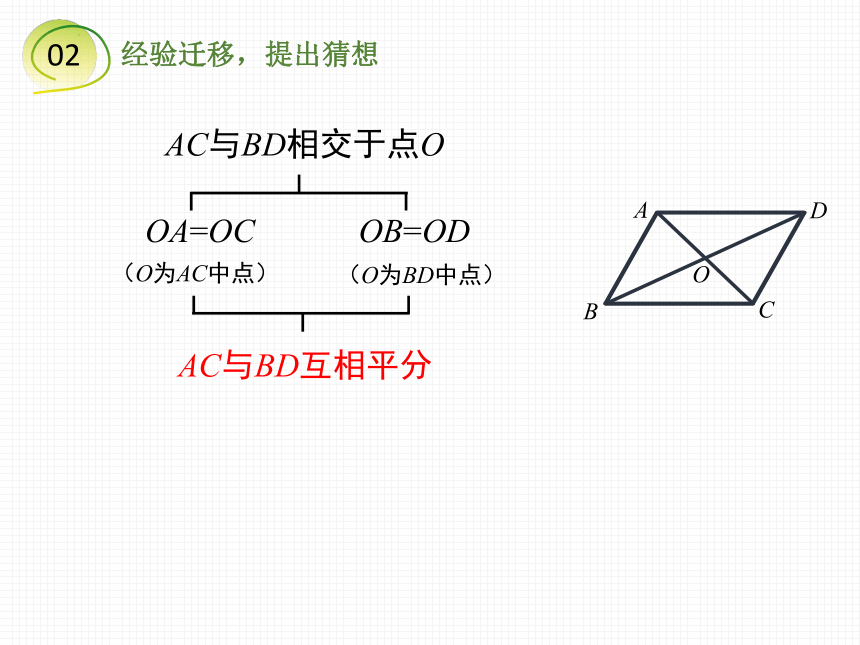
OA=OC
OB=OD
(O为AC中点)
(O为BD中点)
AC与BD相交于点O
AC与BD互相平分
02
经验迁移,提出猜想
A
B
C
D
O
对边
AB=CD,AD=BC
AB=CD,AD=BC
邻角
∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°,∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
发现:
对角线
OA=OC,OB=OD
02
经验迁移,提出猜想
A
B
C
D
O
平行四边形的性质的猜想:
(边)猜想1:平行四边形的对边相等;
(角)猜想2:平行四边形的对角相等;
(对角线)猜想3:平行四边形的对角线互相平分.
02
经验迁移,提出猜想
【活动2】 证明猜想1.
猜想1:平行四边形的对边相等.
题设
结论
如果一个四边形是平行四边形,那么这个四边形的对边相等.
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
03
证明猜想,得出性质
A
B
C
D
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
又 AC=CA,
∴ △ABC≌△CDA(ASA).
∴ AB=CD,AD=BC.
3
4
2
1
03
证明猜想,得出性质
A
B
C
D
性质1:平行四边形的对边相等.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
03
证明猜想,得出性质
证明一个命题的一般步骤
完成证明
阅读命题
分析条件和结论
画出图形
写出符号语言
03
证明猜想,得出性质
连接对角线
构造全等三角形
四边形转化为三角形
连接AC
线段相等
A
B
C
D
A
B
C
D
连接BD
03
证明猜想,得出性质
如果一个四边形是平行四边形,那么这个四边形的对角相等.
猜想2:平行四边形的对角相等.
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
A
B
C
D
活动要求:
(1)小组同学交流证明思路;
(2)独立完成证明过程;
(3)小组派代表进行班级交流展示.
03
证明猜想,得出性质
A
B
C
D
方法1:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ ∠2+∠3=∠1+∠4.
即∠BAD=∠DCB.
∵ AC=CA,
∴ △ABC≌△CDA (ASA).
∴ ∠B=∠D.
3
4
2
1
03
证明猜想,得出性质
A
B
C
D
方法2:∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∴ ∠B+∠C=180°,∠A+∠B=180°.
∴ ∠A=∠C.
同理 ∠B=∠D.
03
证明猜想,得出性质
A
B
C
D
性质2:平行四边形的对角相等.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D.
03
证明猜想,得出性质
猜想3:平行四边形的对角线互相平分.
题设
结论
如果一个四边形是平行四边形,那么这个四边形的对角线互相平分.
已知:如图,在 ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
活动要求:
(1)独立思考并完成证明过程;
(2)小组同学之间互评,评价标准:步骤完整,语言规范、推理严谨;
(3)小组派代表进行班级交流展示.
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB (ASA).
∴ OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
3
4
1
2
性质3:平行四边形的对角线互相平分.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
平行四边形的性质
平行四边形的对边平行
平行四边形的邻角互补
边
角
性质
对角线
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
性质定理
03
证明猜想,得出性质
【活动3】应用练习,巩固新知.
练习:在平行四边形ABCD中,
(1)已知AB=5,BC=3,求它的周长;
A
C
B
D
解:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
又 AB=5,BC=3,
∴ ABCD的周长=AB+BC+CD+DA
=2(AB+BC)
=16.
03
证明猜想,得出性质
练习:在平行四边形ABCD中,
(2)已知∠A=38°,求其余各内角的度数;
解:∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D,AB∥CD.
∴ ∠A+∠D=180°.
∵ ∠A=38°,
∴ ∠C=38°,∠D=142°.
∴ ∠B=142°.
A
C
B
D
03
证明猜想,得出性质
练习:在平行四边形ABCD中,
(3)已知对角线AC,BD相交于点O,AD=10, AC=8,BD=14,求△AOD的周长.
D
A
B
C
O
解:∵ 四边形ABCD是平行四边形,
∴ OA= AC,OD= BD.
又 AC=8,BD=14,
∴ OA=4,OD=7.
∵ AD=10,
∴ △AOD的周长=AD+OA+OD=21.
03
证明猜想,得出性质
回忆本节课,并回答下面的问题:
(1)对平行四边形有了哪些新认识?
(2)平行四边形性质的探究可以从哪些元素出发?
(3)平行四边形性质的探索经历了哪几个阶段?
(4)通过本节课的学习,你对几何图形的研究有什么新的感悟和收获?
04
回顾总结,反思提升
04
回顾总结,反思提升
连接对角线
转化
如何探究平行四边形的性质
提出猜想
类比三角形的性质的研究对象,结合观察和度量
证明猜想
四边形
三角形
(未知)
(已知)
04
回顾总结,反思提升
类比研究
转化
04
回顾总结,反思提升
如果四边形ABCD是平行四边形,AB=6,且AB的长是□ABCD的周长的 .
(1)BC的长为______;
(2)连接AC,BD,相交于点O,则△AOD与△AOB的周长之差为______.
05
课堂检测
A
B
C
D
6
O
10
10
4
同学们再见
·初二数学单元主题教学
探索平行四边形及
特殊的平行四边形的性质
一
探索平行四边形的性质
研究的基本思路
01
激活认识,引入新知
研究的基本思路
01
激活认识,引入新知
三角形
类比研究
直角
三角形
等腰
三角形
等腰
直角
三角形
矩形
菱形
正方形
研究内容
研究对象
定义
性质
判定
边
角
相关的线
互逆命题
角特殊
边特殊
角特殊
边特殊
平行
四边形
边、角
特殊
边、角
特殊
A
B
C
D
平行四边形用“ ”表示,如图,
平行四边形ABCD记作“ ABCD”.
定义:两组对边分别平行的四边形叫做平行四边形.
01
激活认识,引入新知
边
对边
邻边
有公共顶点的边
没有公共顶点的边
定义:两组对边分别平行的四边形叫做平行四边形.
角
对角
邻角
有公共边的角
没有公共边的角
A
B
C
D
01
激活认识,引入新知
∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
01
激活认识,引入新知
【活动1】 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,还可能具有哪些性质?度量一下,和你的猜想一致吗?
平行四边形
的性质
边
角
研究 对象
线
基本
元素
相关元素
活动要求:
(1)独立观察思考,写出猜想;
(2)小组交流,完善猜想;
(3)小组派代表进行班级交流展示.
02
经验迁移,提出猜想
对边
AB∥CD,AD∥BC AB=CD,AD=BC
邻角
∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°,∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
发现:
对角线
OA=OC,OB=OD
A
B
C
D
O
02
经验迁移,提出猜想
OA=OC
OB=OD
(O为AC中点)
(O为BD中点)
AC与BD相交于点O
AC与BD互相平分
02
经验迁移,提出猜想
A
B
C
D
O
对边
AB=CD,AD=BC
AB=CD,AD=BC
邻角
∠A+∠B=180°,∠B+∠C=180°
∠C+∠D=180°,∠A+∠D=180°
∠A=∠C,∠B=∠D
对角
发现:
对角线
OA=OC,OB=OD
02
经验迁移,提出猜想
A
B
C
D
O
平行四边形的性质的猜想:
(边)猜想1:平行四边形的对边相等;
(角)猜想2:平行四边形的对角相等;
(对角线)猜想3:平行四边形的对角线互相平分.
02
经验迁移,提出猜想
【活动2】 证明猜想1.
猜想1:平行四边形的对边相等.
题设
结论
如果一个四边形是平行四边形,那么这个四边形的对边相等.
已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,AD=BC.
A
B
C
D
03
证明猜想,得出性质
A
B
C
D
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
又 AC=CA,
∴ △ABC≌△CDA(ASA).
∴ AB=CD,AD=BC.
3
4
2
1
03
证明猜想,得出性质
A
B
C
D
性质1:平行四边形的对边相等.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
03
证明猜想,得出性质
证明一个命题的一般步骤
完成证明
阅读命题
分析条件和结论
画出图形
写出符号语言
03
证明猜想,得出性质
连接对角线
构造全等三角形
四边形转化为三角形
连接AC
线段相等
A
B
C
D
A
B
C
D
连接BD
03
证明猜想,得出性质
如果一个四边形是平行四边形,那么这个四边形的对角相等.
猜想2:平行四边形的对角相等.
题设
结论
已知:如图,四边形ABCD是平行四边形.
求证:∠A=∠C,∠B=∠D.
A
B
C
D
活动要求:
(1)小组同学交流证明思路;
(2)独立完成证明过程;
(3)小组派代表进行班级交流展示.
03
证明猜想,得出性质
A
B
C
D
方法1:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC,AB∥CD.
∴ ∠1=∠2,∠3=∠4.
∴ ∠2+∠3=∠1+∠4.
即∠BAD=∠DCB.
∵ AC=CA,
∴ △ABC≌△CDA (ASA).
∴ ∠B=∠D.
3
4
2
1
03
证明猜想,得出性质
A
B
C
D
方法2:∵ 四边形ABCD是平行四边形,
∴ AB∥CD,AD∥BC.
∴ ∠B+∠C=180°,∠A+∠B=180°.
∴ ∠A=∠C.
同理 ∠B=∠D.
03
证明猜想,得出性质
A
B
C
D
性质2:平行四边形的对角相等.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D.
03
证明猜想,得出性质
猜想3:平行四边形的对角线互相平分.
题设
结论
如果一个四边形是平行四边形,那么这个四边形的对角线互相平分.
已知:如图,在 ABCD中,对角线AC,BD相交于点O.
求证:OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
活动要求:
(1)独立思考并完成证明过程;
(2)小组同学之间互评,评价标准:步骤完整,语言规范、推理严谨;
(3)小组派代表进行班级交流展示.
证明:∵ 四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB (ASA).
∴ OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
3
4
1
2
性质3:平行四边形的对角线互相平分.
几何语言:
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
A
B
C
D
O
03
证明猜想,得出性质
平行四边形的性质
平行四边形的对边平行
平行四边形的邻角互补
边
角
性质
对角线
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
性质定理
03
证明猜想,得出性质
【活动3】应用练习,巩固新知.
练习:在平行四边形ABCD中,
(1)已知AB=5,BC=3,求它的周长;
A
C
B
D
解:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AD=BC.
又 AB=5,BC=3,
∴ ABCD的周长=AB+BC+CD+DA
=2(AB+BC)
=16.
03
证明猜想,得出性质
练习:在平行四边形ABCD中,
(2)已知∠A=38°,求其余各内角的度数;
解:∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠B=∠D,AB∥CD.
∴ ∠A+∠D=180°.
∵ ∠A=38°,
∴ ∠C=38°,∠D=142°.
∴ ∠B=142°.
A
C
B
D
03
证明猜想,得出性质
练习:在平行四边形ABCD中,
(3)已知对角线AC,BD相交于点O,AD=10, AC=8,BD=14,求△AOD的周长.
D
A
B
C
O
解:∵ 四边形ABCD是平行四边形,
∴ OA= AC,OD= BD.
又 AC=8,BD=14,
∴ OA=4,OD=7.
∵ AD=10,
∴ △AOD的周长=AD+OA+OD=21.
03
证明猜想,得出性质
回忆本节课,并回答下面的问题:
(1)对平行四边形有了哪些新认识?
(2)平行四边形性质的探究可以从哪些元素出发?
(3)平行四边形性质的探索经历了哪几个阶段?
(4)通过本节课的学习,你对几何图形的研究有什么新的感悟和收获?
04
回顾总结,反思提升
04
回顾总结,反思提升
连接对角线
转化
如何探究平行四边形的性质
提出猜想
类比三角形的性质的研究对象,结合观察和度量
证明猜想
四边形
三角形
(未知)
(已知)
04
回顾总结,反思提升
类比研究
转化
04
回顾总结,反思提升
如果四边形ABCD是平行四边形,AB=6,且AB的长是□ABCD的周长的 .
(1)BC的长为______;
(2)连接AC,BD,相交于点O,则△AOD与△AOB的周长之差为______.
05
课堂检测
A
B
C
D
6
O
10
10
4
同学们再见
