湖北省荆州市荆州开发区2022-2023学年高一下学期4月月考数学试卷(Word版含答案)
文档属性
| 名称 | 湖北省荆州市荆州开发区2022-2023学年高一下学期4月月考数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 644.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 22:40:20 | ||
图片预览



文档简介
荆州开发区2022-2023学年高一下学期4月月考
数学试卷
一.单选题
1.已知扇形的周长为6cm,半径是2cm,则扇形的圆心角的弧度数是( )
A. 1 B. 2 C. 3 D. 4
2.若0<α<2π,且sinα<,cosα>,则角α的取值范围是( )
A. B.
C. D. ∪
3.化简( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.函数的图象大致是( )
A. B.
C. D.
6.函数f(x)=Asin(ωx+)(ω>0)的部分图象如图,f(x)的最小正零点是,f(x)的单调递增区间是( )
A. (k∈Z ) B.(k∈Z)
C.(k∈Z) D.(k∈Z)
7.
已知函数若函数()恰有4个零点,分别为x1,x2,x3,x4,且,则的取值范围是()
A. B. C. D.
8.
若关于x的不等式在上恒成立,则m的取值范围为()
A. B. C. D.
二.多选题
9.下列计算中正确的是( )
A. B.
C. D.
10.已知曲线:,:,则( )
A.把向左平移个单位长度,再将所有点的横坐标变为原来的2倍,得到
B.把向左平移个单位长度,再将所有点的横坐标变为原来的倍,得到
C.把上所有点的横坐标变为原来的倍,再向左平移个单位长度,得到
D.把上所有点的横坐标变为原来的倍,再向左平移个单位长度,得到
11.(多选)已知,,则( )
A. B.
C. D.
12.已知函数的图象关于直线对称,且对于,当,,且时,恒成立.若对任意的恒成立,则实数a的范围可以是下面选项中的( )
A. B. C. D.
三、填空题(本题共4道小题,
13.函数的定义域为______.
14.已知函数是定义在R上的单调递增函数,则实数a的取值范围是
15.已知,则______.
16.函数的所有零点之和为__________.
四、解答题
17.已知且求及
18.已知,且,.
(1)求的值;
(2)求的值.
19.已知函数的部分图象如图所示,且在处取得最大值,图象与轴交于点.
(1)求函数f(x)的解析式;
(2)若,且,求的值.
20.
2021年3月1日,国务院新闻办公室举行新闻发布会,工业和信息化部提出了芯片发展的五项措施,进一步激励国内科技巨头加大了科技研发投入的力度.根据市场调查某数码产品公司生产某款运动手环的年固定成本为50万元,每生产1万只还需另投入20万元.若该公司一年内共生产该款运动手环万只并能全部销售完,平均每万只的销售投入为万元,且.当该公司一年内共生产该款运动手环5万只并全部销售完时,年利润为300万元.
(1)求出的值并写出年利润(万元)关于年产量(万部)的函数解析式;
(2)当年产量为多少万只时,公司在该款运动手环的生产中所获得的利润最大?并求出最大利润.
21.已知函数.
(1)当时,解不等式;
(2)若函数的图象过点,且关于的方程有实根,求实数的取值范围.
22.
已知.
(1)求f(x)的单调递增区间;
(2)若对任意的恒成立,求a的取值范围.
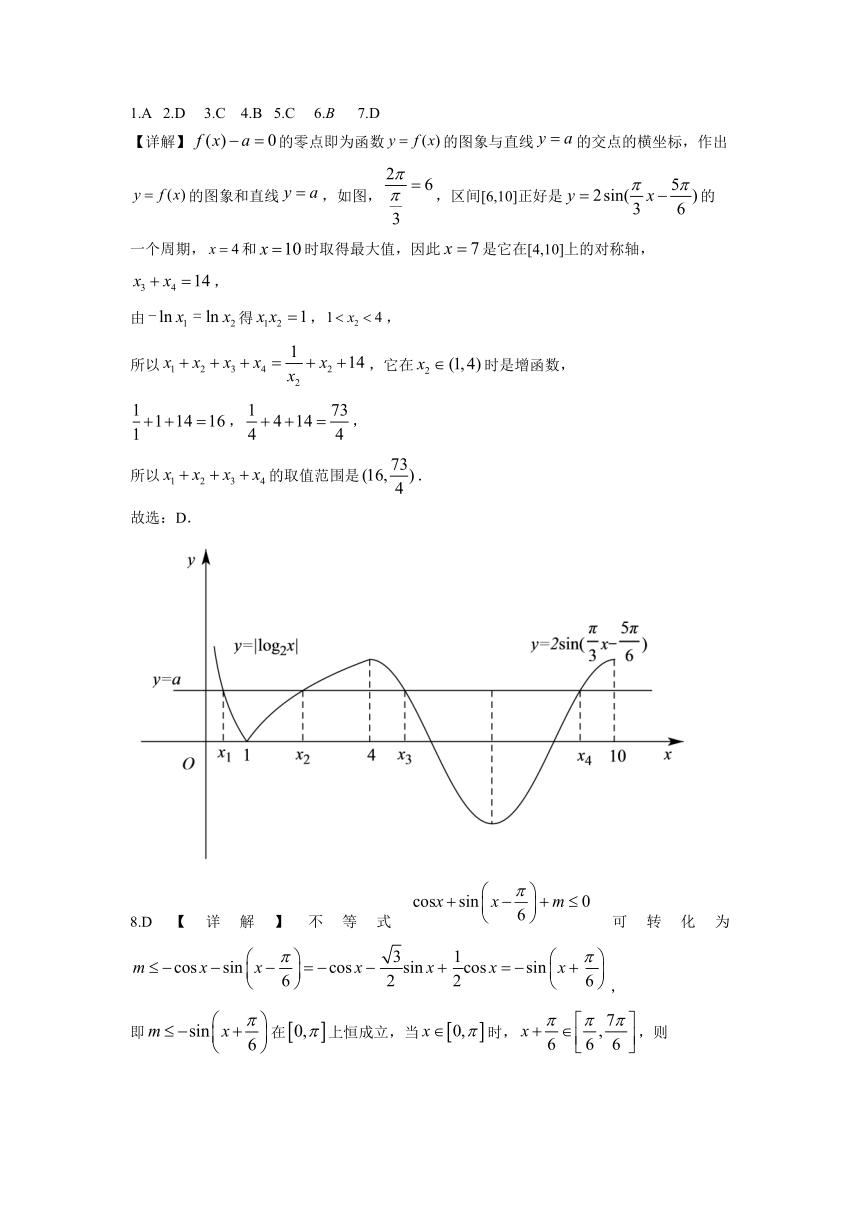
1.A 2.D 3.C 4.B 5.C 6.B 7.D
【详解】的零点即为函数的图象与直线的交点的横坐标,作出的图象和直线,如图,,区间[6,10]正好是的一个周期,和时取得最大值,因此是它在[4,10]上的对称轴,,
由得,,
所以,它在时是增函数,
,,
所以的取值范围是.
故选:D.
8.D【详解】不等式可转化为,
即在上恒成立,当时,,则,则.
9.ABCD
10.BD【详解】变换方式一:将函数的图象向左平移个单位长度,得到的图象,再将所有点的横坐标变为原来的倍,得到曲线.
变换方式二:因为,所以将函数的图象上所有点的横坐标变为原来的倍,得到的图象,再向左平移个单位长度,得到曲线.
故选:BD.
11.ABD
已知式平方求得,从而可确定的范围,然后求得,再与已知结合求得,由商数关系得,从而可判断各选项.
【详解】因为①,所以,所以.又,所以,所以,即,故A正确.,所以②,故D正确.由①②,得,,故B正确.,故C错误.
故选:ABD.
12.ABC
首先得到为偶函数且在上单调递增,则在上单调递减,则问题转化为恒成立,再根据一元二次不等式恒成立求出参数的取值范围.
【详解】解:因为函数的图象关于直线对称,所以的图象关于轴对称,即为偶函数,
又当,,且时,恒成立,即恒成立,
所以在上单调递增,则在上单调递减,
若对任意的恒成立,
即恒成立,即恒成立,
即恒成立,即,解得,即,
故符合条件的有A、B、C;
故选:ABC
13. 14.
所以当时,在上单调递增,
又因为f(x)开口向下,对称轴为,
所以,故,且在上的最大值为,
当时,在上单调递增,
所以由幂函数的性质可知,且,
故,得,
由于以上条件要同时成立,故,即.
15.
【详解】.
16.9
【详解】由,令,,
显然与的图象都关于直线对称,
在同一坐标系内作出函数,的图象,如图,
观察图象知,函数,的图象有6个公共点,其横坐标依次为,
这6个点两两关于直线对称,有,则,
所以函数的所有零点之和为9.
故答案为:9
17.
由,则,即,
,
.
18.
(1)因为,所以.
(2)因为,
所以,
所以,
所以,
因为,所以,
所以.
19.(1)由图象可知函数的周期为,所以.
又因为函数在处取得最大值
所以,所以,
因为,所以,
故.
又因为,所以,
所以.
(2)由(1)有,
因为,则,
由于,从而,
因此.
所以
20.
(1)由题意可得
当时,所以
解得
所以
(2)当时,,其对称轴为
所以当时取得最大值750万元
当时,万元
当且仅当即时等号成立
因为
所以当年产量为30万只时,公司在该款运动手环的生产中所获得的利润最大,最大利润为850万元.
21.(1)当时,.
由,
得,
得,
得,
解得.
故不等式的解集是.
(2)因为函数的图象过点,
所以,
即,
解得.
所以.
因为关于的方程有实根,
即有实根.
所以方程有实根..
令,
则.
因为,,
所以的值域为.
所以,
解得.
所以实数的取值范围是.
22.(1)化简得
,
令,,解得,
所以单调递增区间为,.
(2)由(1)可得,
即,对任意的恒成立,
只需要即可,
,
令,,为减函数,
所以当时,,
所以.
数学试卷
一.单选题
1.已知扇形的周长为6cm,半径是2cm,则扇形的圆心角的弧度数是( )
A. 1 B. 2 C. 3 D. 4
2.若0<α<2π,且sinα<,cosα>,则角α的取值范围是( )
A. B.
C. D. ∪
3.化简( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.函数的图象大致是( )
A. B.
C. D.
6.函数f(x)=Asin(ωx+)(ω>0)的部分图象如图,f(x)的最小正零点是,f(x)的单调递增区间是( )
A. (k∈Z ) B.(k∈Z)
C.(k∈Z) D.(k∈Z)
7.
已知函数若函数()恰有4个零点,分别为x1,x2,x3,x4,且,则的取值范围是()
A. B. C. D.
8.
若关于x的不等式在上恒成立,则m的取值范围为()
A. B. C. D.
二.多选题
9.下列计算中正确的是( )
A. B.
C. D.
10.已知曲线:,:,则( )
A.把向左平移个单位长度,再将所有点的横坐标变为原来的2倍,得到
B.把向左平移个单位长度,再将所有点的横坐标变为原来的倍,得到
C.把上所有点的横坐标变为原来的倍,再向左平移个单位长度,得到
D.把上所有点的横坐标变为原来的倍,再向左平移个单位长度,得到
11.(多选)已知,,则( )
A. B.
C. D.
12.已知函数的图象关于直线对称,且对于,当,,且时,恒成立.若对任意的恒成立,则实数a的范围可以是下面选项中的( )
A. B. C. D.
三、填空题(本题共4道小题,
13.函数的定义域为______.
14.已知函数是定义在R上的单调递增函数,则实数a的取值范围是
15.已知,则______.
16.函数的所有零点之和为__________.
四、解答题
17.已知且求及
18.已知,且,.
(1)求的值;
(2)求的值.
19.已知函数的部分图象如图所示,且在处取得最大值,图象与轴交于点.
(1)求函数f(x)的解析式;
(2)若,且,求的值.
20.
2021年3月1日,国务院新闻办公室举行新闻发布会,工业和信息化部提出了芯片发展的五项措施,进一步激励国内科技巨头加大了科技研发投入的力度.根据市场调查某数码产品公司生产某款运动手环的年固定成本为50万元,每生产1万只还需另投入20万元.若该公司一年内共生产该款运动手环万只并能全部销售完,平均每万只的销售投入为万元,且.当该公司一年内共生产该款运动手环5万只并全部销售完时,年利润为300万元.
(1)求出的值并写出年利润(万元)关于年产量(万部)的函数解析式;
(2)当年产量为多少万只时,公司在该款运动手环的生产中所获得的利润最大?并求出最大利润.
21.已知函数.
(1)当时,解不等式;
(2)若函数的图象过点,且关于的方程有实根,求实数的取值范围.
22.
已知.
(1)求f(x)的单调递增区间;
(2)若对任意的恒成立,求a的取值范围.
1.A 2.D 3.C 4.B 5.C 6.B 7.D
【详解】的零点即为函数的图象与直线的交点的横坐标,作出的图象和直线,如图,,区间[6,10]正好是的一个周期,和时取得最大值,因此是它在[4,10]上的对称轴,,
由得,,
所以,它在时是增函数,
,,
所以的取值范围是.
故选:D.
8.D【详解】不等式可转化为,
即在上恒成立,当时,,则,则.
9.ABCD
10.BD【详解】变换方式一:将函数的图象向左平移个单位长度,得到的图象,再将所有点的横坐标变为原来的倍,得到曲线.
变换方式二:因为,所以将函数的图象上所有点的横坐标变为原来的倍,得到的图象,再向左平移个单位长度,得到曲线.
故选:BD.
11.ABD
已知式平方求得,从而可确定的范围,然后求得,再与已知结合求得,由商数关系得,从而可判断各选项.
【详解】因为①,所以,所以.又,所以,所以,即,故A正确.,所以②,故D正确.由①②,得,,故B正确.,故C错误.
故选:ABD.
12.ABC
首先得到为偶函数且在上单调递增,则在上单调递减,则问题转化为恒成立,再根据一元二次不等式恒成立求出参数的取值范围.
【详解】解:因为函数的图象关于直线对称,所以的图象关于轴对称,即为偶函数,
又当,,且时,恒成立,即恒成立,
所以在上单调递增,则在上单调递减,
若对任意的恒成立,
即恒成立,即恒成立,
即恒成立,即,解得,即,
故符合条件的有A、B、C;
故选:ABC
13. 14.
所以当时,在上单调递增,
又因为f(x)开口向下,对称轴为,
所以,故,且在上的最大值为,
当时,在上单调递增,
所以由幂函数的性质可知,且,
故,得,
由于以上条件要同时成立,故,即.
15.
【详解】.
16.9
【详解】由,令,,
显然与的图象都关于直线对称,
在同一坐标系内作出函数,的图象,如图,
观察图象知,函数,的图象有6个公共点,其横坐标依次为,
这6个点两两关于直线对称,有,则,
所以函数的所有零点之和为9.
故答案为:9
17.
由,则,即,
,
.
18.
(1)因为,所以.
(2)因为,
所以,
所以,
所以,
因为,所以,
所以.
19.(1)由图象可知函数的周期为,所以.
又因为函数在处取得最大值
所以,所以,
因为,所以,
故.
又因为,所以,
所以.
(2)由(1)有,
因为,则,
由于,从而,
因此.
所以
20.
(1)由题意可得
当时,所以
解得
所以
(2)当时,,其对称轴为
所以当时取得最大值750万元
当时,万元
当且仅当即时等号成立
因为
所以当年产量为30万只时,公司在该款运动手环的生产中所获得的利润最大,最大利润为850万元.
21.(1)当时,.
由,
得,
得,
得,
解得.
故不等式的解集是.
(2)因为函数的图象过点,
所以,
即,
解得.
所以.
因为关于的方程有实根,
即有实根.
所以方程有实根..
令,
则.
因为,,
所以的值域为.
所以,
解得.
所以实数的取值范围是.
22.(1)化简得
,
令,,解得,
所以单调递增区间为,.
(2)由(1)可得,
即,对任意的恒成立,
只需要即可,
,
令,,为减函数,
所以当时,,
所以.
同课章节目录
