第6章 数据分析期末复习课件
图片预览





文档简介
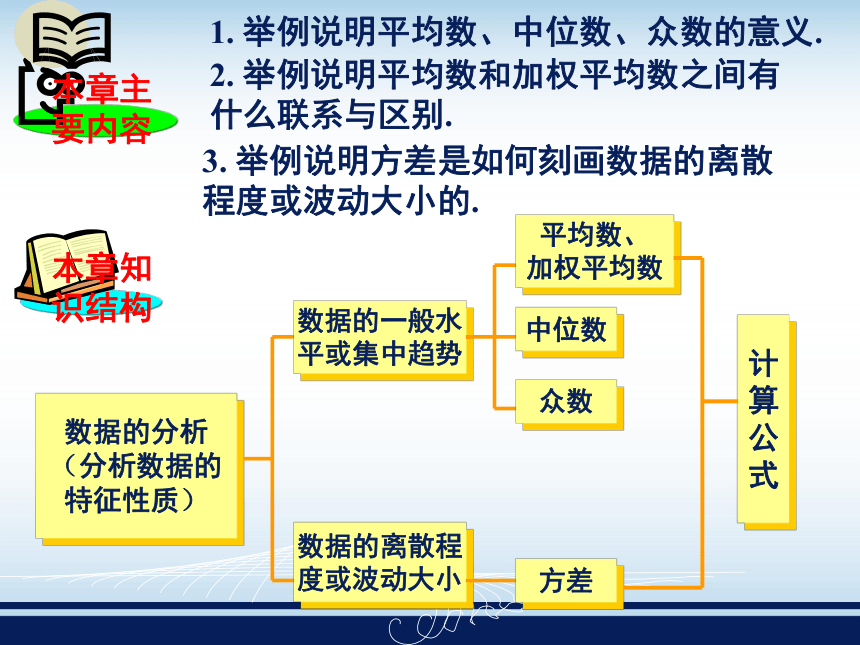
课件19张PPT。1. 举例说明平均数、中位数、众数的意义.2. 举例说明平均数和加权平均数之间有什么联系与区别.3. 举例说明方差是如何刻画数据的离散程度或波动大小的.数据的分析
(分析数据的
特征性质)数据的一般水
平或集中趋势数据的离散程
度或波动大小平均数、
加权平均数中位数众数方差计
算
公
式对于一组数据x1,x2,x3,…,xn,
并且他们的权数分别是f1,f2,f3,…,fn,则有(算术平均数)(加权平均数,
其中f1+f2+f3+…+fn=n)将一组数据按从小到大的顺序排列起来,处于最中间位置
的一个数(或中间两个数的平均数); 众数:数据组中出现次数最多的数,它可能是其中的一个数或多个数; 反映一组数据的波动大小,计算公式: 平均数、中位数、众数都是一组数据的代表,它们从不同侧面反映了数据的一般水平或集中趋势. 平均数:中位数方 差:1. 平均数与加权平均数的意义不同. 当一组数据中不同的数重复出现时,我们用权数的大小来反映重复次数的多少; 通常也用权数来反映一组数据中不同成分的比例或重要性. 对于不同的实际问题,权数常有不同的含义.2. 平均数、中位数、众数都是一组数据的代表,它们从不同侧面反映了数据的一般水平或集中趋势. 值得注意的是:平均数相同的数据组在性质上仍可能有很大的区别,这是因为它们相对于平均数的分布情况不同,即数据组中的数相对于平均数的偏差不同.方差是一组数据中各数与其平均数之差的平方的平均值,它反映了一组数据在其平均数周围的离散程度.④数据2x1-3,2x2-3,2x3-3,…2xn-3的平均数为 ,
方差为 , 把一组数据每个数都加上一个数a,那么平均数增加a,方差不变。
每个数据扩大为原来的n倍,那么平均数为原来的n倍,方差是原来的n2倍。变式规律已知数据x1,x2,x3,… xn的平均数为a,方差为b,则①数据x1+3,x2+3,x3+3,…,xn+3的平均数为 ,
方差为 ,②数据x1-3,x2-3,x3-3,…xn-3的平均数为 ,
方差为 ,③数据4x1,4x2,4x3,…,4xn的平均数为 ,
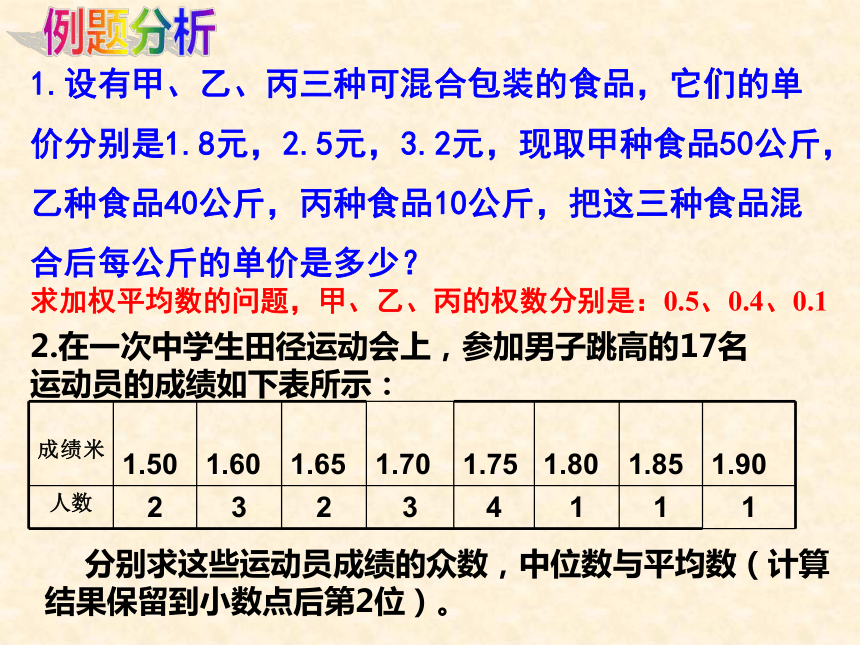
方差为 ,a+3a-34a2a-3bb16b4b例题分析设有甲、乙、丙三种可混合包装的食品,它们的单价分别是1.8元,2.5元,3.2元,现取甲种食品50公斤,乙种食品40公斤,丙种食品10公斤,把这三种食品混合后每公斤的单价是多少? 求加权平均数的问题,甲、乙、丙的权数分别是:0.5、0.4、0.12.在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示: 分别求这些运动员成绩的众数,中位数与平均数(计算结果保留到小数点后第2位)。 3. 中考后,老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计表。
得分率=得该分数的人数/被统计的人数。 (1)估计该题能得2分或2分以上者,即可认为“比较好”,在所统计的学生中共有224人不属于“比较 好”。问统计的总人数为多少?(2)求该题得分的众数、中位数和平均数。分析:(1)“比较好”的占55.2%即可求出总人数。
(2)众数、中位数可由所占比例得出,
平均得分即求加权平均数5.某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定。现从两家提供的样品中各抽查10件,测得它们得质量如下(单位:g)甲:500,499,500,500,503,498,497,502,500,501;乙:499, 500,498,501,500,501,500,499,500,502。你认为应该选择哪一家制造厂承担外销业务?S2甲=2.8S2乙=1.2,所以选乙6.某校要从甲、乙两名跳高运动员中挑选一人参加一项校际比赛,
在最近的8次选拔赛中,他们的成绩(单位:m)如下:
甲:1.70,1.65,1.68,1.69,1.72,1.73,1.68,1.67
乙:1.60,1.73,1.72,1.61,1.62,1.71,1.70,1.75
(1)他们的平均成绩分别是多少?
(2)哪个人的成绩更为稳定?
(3)经预测,跳高1.65m就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?若预测跳高1.70m方可获得冠军呢? S2甲=0.0006S2乙=0.00315练一练1.数据 35,35,35,47,47,84,84,84,84,125的平均数是 。66 2.近年来,我市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为______.223.在一组数据 1,0,4,5,8中插入一个数据x,使该组数据的中位数为3,则插入数据x 是 。26. 已知数据x1,x2,x3,…xn的平均数为3,方差为4,则数据5x1+3,
5x2+3,5x3+3,…5xn+3的平均数为 ,方差为______. 181005.已知一组数据2,1,-1,0,3,则这组数据的方差是______.4.某市的7月下旬最高气温统计如下:该市7月中旬最高气温的平均数是_____。332填空题8.有一组数据,各个数据之和为505,如果它们的平均数为101,那么这组数据的个数为_____.7.若4,x,5的平均数是7,则3,4,5,x,6这五个数的平均数是___659. 5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是_ .8010.某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:(1)填写下表11233451 (2)这20个家庭的年平均收入为————万元。关于年收入
数据中的中位数是————万元,众数是————万元。1.61.21.31.一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72C2.某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、68 D、70D3.小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )A、小明体重是45kgB、小明比小亮重3kgC、小明体重不能确定D、小明与小亮体重相等C选择题4.当5个整数从小到大排列,其中位数是4,如果这个数集的唯一众数是6,则这5个整数可能的最大的和是( )。
A.21 B.22 C.23 D.24。AD6.在某城市,80%的家庭收入不少于2.5万元,下面一定不少于2.5万元的是( )A. 年收入的平均数 B. 年收入的众数
C. 年收入的中位数 D. 年收入的平均数和众数C7. 某班在一次数学测试后,成绩统计如下表:该班这次数学测试的平均成绩是: ( )A. 82分 B.75 分 C.65 分 D.62分A8. 某人旅行100千米,前50千米的速度为100千米/时,后50千米的速度为120千米/时,则此人的平均速度估计为( )A. 100千米/时 B.109千米/时 C.110千米/时 D.115千米/时B9.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差 是1.8.下列说法中正确的是( )
A.甲、乙射中的总环数不相同 B.甲的成绩较稳定
C.乙的成绩波动较小 D.甲、乙的众数相同B10.数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据
图表,全班每位同学答对的
题数的中位数和众数分别为
( )
A 8,8 B 8,9
C 9,9 D 9,8D解答题1.在一个班的40名学生中,14岁的有5人,15岁的有30人,16岁的有4人,17岁的有1人。求这个班学生的平均年龄。3.求下列数据的方差。
(1)5,9,7,6,8
(2)300,301,302,301,2992.求下列各组数的平均数:谈谈你的体会?
(1)105,103,101,100,114,108,110, 106,98,102;
(2)4203,4204,4200,4194,4204,4210,4195,4199.4.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的平均数和方差。 5.某公司欲招聘一名公关人员,对甲、乙两名候选人进行了面试和笔试,他们的成绩如下表所示:(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?(2)如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁被录取?甲将被录取乙将被录取6.某商场销售了一批女鞋30双,其中各种尺码的销售量如下表所示:(1)计算30双女鞋尺寸的平均数、中位数、众数?
(2)请问此商场的经理关注的是这组数据的平均数吗?他关注的是什么?为什么?若你是经理,你将如何调整进货数量呢?
7.八年级要举行篮球投篮比赛,每班各派一名代表参加,根据在3分钟时间内投中个数决定出胜负。某班先预选出甲、乙两两位同学,在相同的条件下各投篮10次,每次投篮的成绩情况如下表所示:(1)请填写下表:(2)请从不同的角度对这次测试结果进行分析;(3)你将选谁参加比赛?说说你的理由。77.5705.41.2
8.某农场种植甲、乙两种不同品种的水稻,6年中各年每亩的平均产量如下(单位:kg)
甲:450,458,450,425,455,462;
乙:446,476,473,429,432,444.
问哪一个品种水稻的产量比较稳定? 1.A公司和B公司去年用于工人工资、培训费用、保险支出均分别为72万元、36万元和12万元。 A公司今年这3项支出依次比去年增长了10%、20%和30%, B公司今年这3项支出依次比去年增长了30%、10%和20%, A、B公司今年这3项总支出比去年增长的百分数相等吗?它们分别是多少?2.有十五位同学参加竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数以后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛?3.工厂有15名工人,某一天他们生产的机器零件个数统计如下:为了提高工作效率和工人的积极性,管理者准备实行每天生产定额,超产有奖的措施。如果你是管理者,你将如何确定这个“定额”?你需要考虑哪些统计量?平均数是:约10.1个中位数是:9个众数是:8个现在你确定的“定额”是————个?说说你的想法!注意!在实际情景中,车间管理者在决策时可能还需要考虑其他一些因素,如技术的更新、工人素质的提高等。4.甲、乙两个小组各10名学生某次数学测试成绩 如下(单位:分)
甲组:76、90、84、86、81、87、86、82、85、83;
乙组:82、84、85、89、79、80、91、89、79、74。
请你选用合适的统计量,对这两组学生的这次测试成绩作出评价。主要对平均数、方差这两个数据比较,
从两组学生成绩的平均状态和稳定性做出评价。作业:P156------P158复习题
(分析数据的
特征性质)数据的一般水
平或集中趋势数据的离散程
度或波动大小平均数、
加权平均数中位数众数方差计
算
公
式对于一组数据x1,x2,x3,…,xn,
并且他们的权数分别是f1,f2,f3,…,fn,则有(算术平均数)(加权平均数,
其中f1+f2+f3+…+fn=n)将一组数据按从小到大的顺序排列起来,处于最中间位置
的一个数(或中间两个数的平均数); 众数:数据组中出现次数最多的数,它可能是其中的一个数或多个数; 反映一组数据的波动大小,计算公式: 平均数、中位数、众数都是一组数据的代表,它们从不同侧面反映了数据的一般水平或集中趋势. 平均数:中位数方 差:1. 平均数与加权平均数的意义不同. 当一组数据中不同的数重复出现时,我们用权数的大小来反映重复次数的多少; 通常也用权数来反映一组数据中不同成分的比例或重要性. 对于不同的实际问题,权数常有不同的含义.2. 平均数、中位数、众数都是一组数据的代表,它们从不同侧面反映了数据的一般水平或集中趋势. 值得注意的是:平均数相同的数据组在性质上仍可能有很大的区别,这是因为它们相对于平均数的分布情况不同,即数据组中的数相对于平均数的偏差不同.方差是一组数据中各数与其平均数之差的平方的平均值,它反映了一组数据在其平均数周围的离散程度.④数据2x1-3,2x2-3,2x3-3,…2xn-3的平均数为 ,
方差为 , 把一组数据每个数都加上一个数a,那么平均数增加a,方差不变。
每个数据扩大为原来的n倍,那么平均数为原来的n倍,方差是原来的n2倍。变式规律已知数据x1,x2,x3,… xn的平均数为a,方差为b,则①数据x1+3,x2+3,x3+3,…,xn+3的平均数为 ,
方差为 ,②数据x1-3,x2-3,x3-3,…xn-3的平均数为 ,
方差为 ,③数据4x1,4x2,4x3,…,4xn的平均数为 ,
方差为 ,a+3a-34a2a-3bb16b4b例题分析设有甲、乙、丙三种可混合包装的食品,它们的单价分别是1.8元,2.5元,3.2元,现取甲种食品50公斤,乙种食品40公斤,丙种食品10公斤,把这三种食品混合后每公斤的单价是多少? 求加权平均数的问题,甲、乙、丙的权数分别是:0.5、0.4、0.12.在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示: 分别求这些运动员成绩的众数,中位数与平均数(计算结果保留到小数点后第2位)。 3. 中考后,老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计表。
得分率=得该分数的人数/被统计的人数。 (1)估计该题能得2分或2分以上者,即可认为“比较好”,在所统计的学生中共有224人不属于“比较 好”。问统计的总人数为多少?(2)求该题得分的众数、中位数和平均数。分析:(1)“比较好”的占55.2%即可求出总人数。
(2)众数、中位数可由所占比例得出,
平均得分即求加权平均数5.某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定。现从两家提供的样品中各抽查10件,测得它们得质量如下(单位:g)甲:500,499,500,500,503,498,497,502,500,501;乙:499, 500,498,501,500,501,500,499,500,502。你认为应该选择哪一家制造厂承担外销业务?S2甲=2.8S2乙=1.2,所以选乙6.某校要从甲、乙两名跳高运动员中挑选一人参加一项校际比赛,
在最近的8次选拔赛中,他们的成绩(单位:m)如下:
甲:1.70,1.65,1.68,1.69,1.72,1.73,1.68,1.67
乙:1.60,1.73,1.72,1.61,1.62,1.71,1.70,1.75
(1)他们的平均成绩分别是多少?
(2)哪个人的成绩更为稳定?
(3)经预测,跳高1.65m就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?若预测跳高1.70m方可获得冠军呢? S2甲=0.0006S2乙=0.00315练一练1.数据 35,35,35,47,47,84,84,84,84,125的平均数是 。66 2.近年来,我市民用汽车拥有量持续增长,2007年至2011年我市民用汽车拥有量依次约11,13,15,19,x(单位:万辆),这五个数的平均数为16,则x的值为______.223.在一组数据 1,0,4,5,8中插入一个数据x,使该组数据的中位数为3,则插入数据x 是 。26. 已知数据x1,x2,x3,…xn的平均数为3,方差为4,则数据5x1+3,
5x2+3,5x3+3,…5xn+3的平均数为 ,方差为______. 181005.已知一组数据2,1,-1,0,3,则这组数据的方差是______.4.某市的7月下旬最高气温统计如下:该市7月中旬最高气温的平均数是_____。332填空题8.有一组数据,各个数据之和为505,如果它们的平均数为101,那么这组数据的个数为_____.7.若4,x,5的平均数是7,则3,4,5,x,6这五个数的平均数是___659. 5个数据的和为405,其中一个数据为85,那么另4个数据的平均数是_ .8010.某同学进行社会调查,随机抽查某地区20个家庭的收入情况,并绘制了统计图请根据统计图给出的信息回答:(1)填写下表11233451 (2)这20个家庭的年平均收入为————万元。关于年收入
数据中的中位数是————万元,众数是————万元。1.61.21.31.一组数据:40、37、x、64的平均数是53,则x的值是( )
A、67 B、69 C、71 D、72C2.某次考试A、B、C、D、E五名学生平均分为62分,除A以外四人平均分为60分,则A得分为( )
A、60 B、62 C、68 D、70D3.小明所在班级的男同学的平均体重是45kg,小亮所在班级的男同学的平均体重是42kg,则下列判断正确的是( )A、小明体重是45kgB、小明比小亮重3kgC、小明体重不能确定D、小明与小亮体重相等C选择题4.当5个整数从小到大排列,其中位数是4,如果这个数集的唯一众数是6,则这5个整数可能的最大的和是( )。
A.21 B.22 C.23 D.24。AD6.在某城市,80%的家庭收入不少于2.5万元,下面一定不少于2.5万元的是( )A. 年收入的平均数 B. 年收入的众数
C. 年收入的中位数 D. 年收入的平均数和众数C7. 某班在一次数学测试后,成绩统计如下表:该班这次数学测试的平均成绩是: ( )A. 82分 B.75 分 C.65 分 D.62分A8. 某人旅行100千米,前50千米的速度为100千米/时,后50千米的速度为120千米/时,则此人的平均速度估计为( )A. 100千米/时 B.109千米/时 C.110千米/时 D.115千米/时B9.甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差 是1.8.下列说法中正确的是( )
A.甲、乙射中的总环数不相同 B.甲的成绩较稳定
C.乙的成绩波动较小 D.甲、乙的众数相同B10.数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据
图表,全班每位同学答对的
题数的中位数和众数分别为
( )
A 8,8 B 8,9
C 9,9 D 9,8D解答题1.在一个班的40名学生中,14岁的有5人,15岁的有30人,16岁的有4人,17岁的有1人。求这个班学生的平均年龄。3.求下列数据的方差。
(1)5,9,7,6,8
(2)300,301,302,301,2992.求下列各组数的平均数:谈谈你的体会?
(1)105,103,101,100,114,108,110, 106,98,102;
(2)4203,4204,4200,4194,4204,4210,4195,4199.4.已知一组数据10,10,x,8(由大到小排列)的中位数与平均数相等,求x值及这组数据的平均数和方差。 5.某公司欲招聘一名公关人员,对甲、乙两名候选人进行了面试和笔试,他们的成绩如下表所示:(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?(2)如果公司认为,作为公关人员面试的成绩比笔试的成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁被录取?甲将被录取乙将被录取6.某商场销售了一批女鞋30双,其中各种尺码的销售量如下表所示:(1)计算30双女鞋尺寸的平均数、中位数、众数?
(2)请问此商场的经理关注的是这组数据的平均数吗?他关注的是什么?为什么?若你是经理,你将如何调整进货数量呢?
7.八年级要举行篮球投篮比赛,每班各派一名代表参加,根据在3分钟时间内投中个数决定出胜负。某班先预选出甲、乙两两位同学,在相同的条件下各投篮10次,每次投篮的成绩情况如下表所示:(1)请填写下表:(2)请从不同的角度对这次测试结果进行分析;(3)你将选谁参加比赛?说说你的理由。77.5705.41.2
8.某农场种植甲、乙两种不同品种的水稻,6年中各年每亩的平均产量如下(单位:kg)
甲:450,458,450,425,455,462;
乙:446,476,473,429,432,444.
问哪一个品种水稻的产量比较稳定? 1.A公司和B公司去年用于工人工资、培训费用、保险支出均分别为72万元、36万元和12万元。 A公司今年这3项支出依次比去年增长了10%、20%和30%, B公司今年这3项支出依次比去年增长了30%、10%和20%, A、B公司今年这3项总支出比去年增长的百分数相等吗?它们分别是多少?2.有十五位同学参加竞赛,且他们的分数互不相同,取八位同学进入决赛,某人知道了自己的分数以后,还需知道这十五位同学的分数的什么量,就能判断他能不能进入决赛?3.工厂有15名工人,某一天他们生产的机器零件个数统计如下:为了提高工作效率和工人的积极性,管理者准备实行每天生产定额,超产有奖的措施。如果你是管理者,你将如何确定这个“定额”?你需要考虑哪些统计量?平均数是:约10.1个中位数是:9个众数是:8个现在你确定的“定额”是————个?说说你的想法!注意!在实际情景中,车间管理者在决策时可能还需要考虑其他一些因素,如技术的更新、工人素质的提高等。4.甲、乙两个小组各10名学生某次数学测试成绩 如下(单位:分)
甲组:76、90、84、86、81、87、86、82、85、83;
乙组:82、84、85、89、79、80、91、89、79、74。
请你选用合适的统计量,对这两组学生的这次测试成绩作出评价。主要对平均数、方差这两个数据比较,
从两组学生成绩的平均状态和稳定性做出评价。作业:P156------P158复习题
