三角形的中位线[下学期]
图片预览



文档简介
课件22张PPT。A 。。BC 。D。。
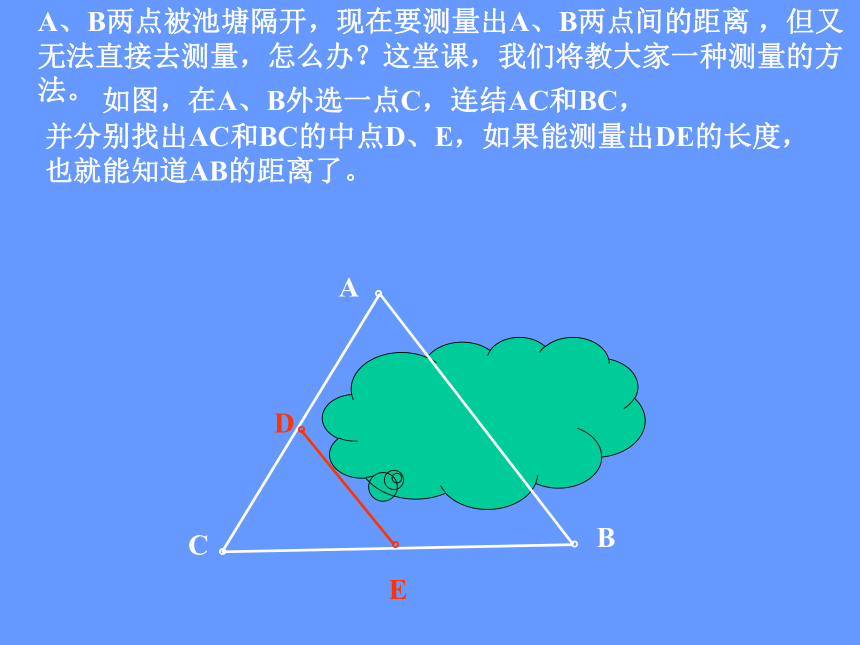
E如图,在A、B外选一点C,连结AC和BC,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将教大家一种测量的方法。并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。三角形的中位线和三角形的中线
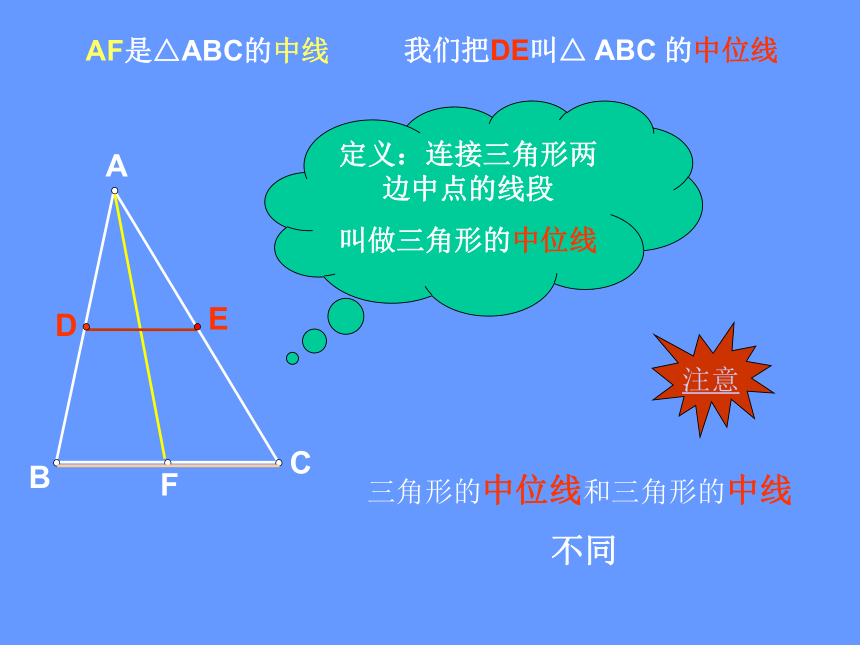
不同CBAFED定义:连接三角形两边中点的线段
叫做三角形的中位线
AF是△ABC的中线我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段 区分三角形的中位线和中线: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FE点是线段AC的中点
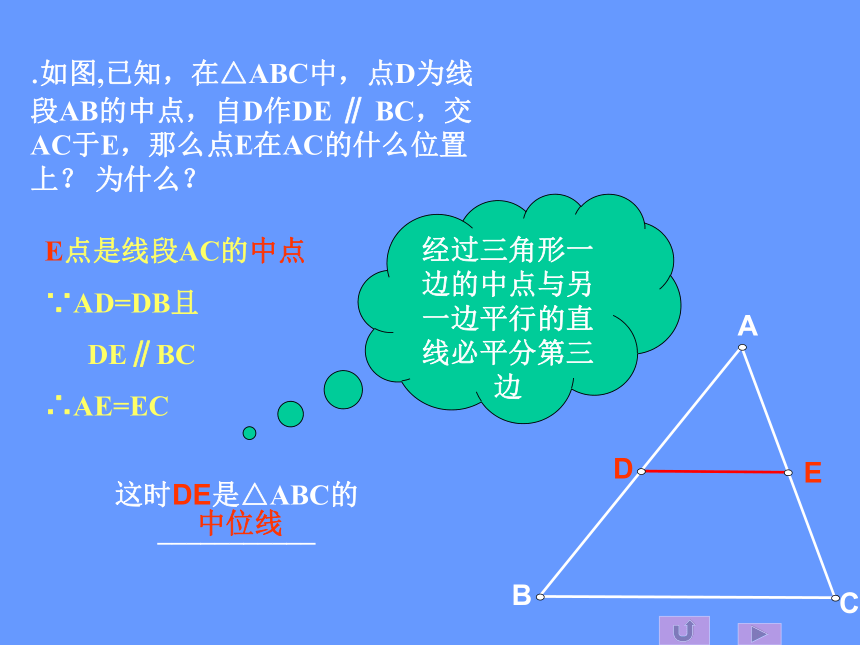
∵AD=DB且
DE∥BC
∴AE=EC ABCDE经过三角形一边的中点与另一边平行的直线必平分第三边.如图,已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?这时DE是△ABC的___________中位线三角形的中位线平行于第三边,并且等于第三边的 一半ABCDEF已知:在△ABC 中,DE是△ABC 的中位线
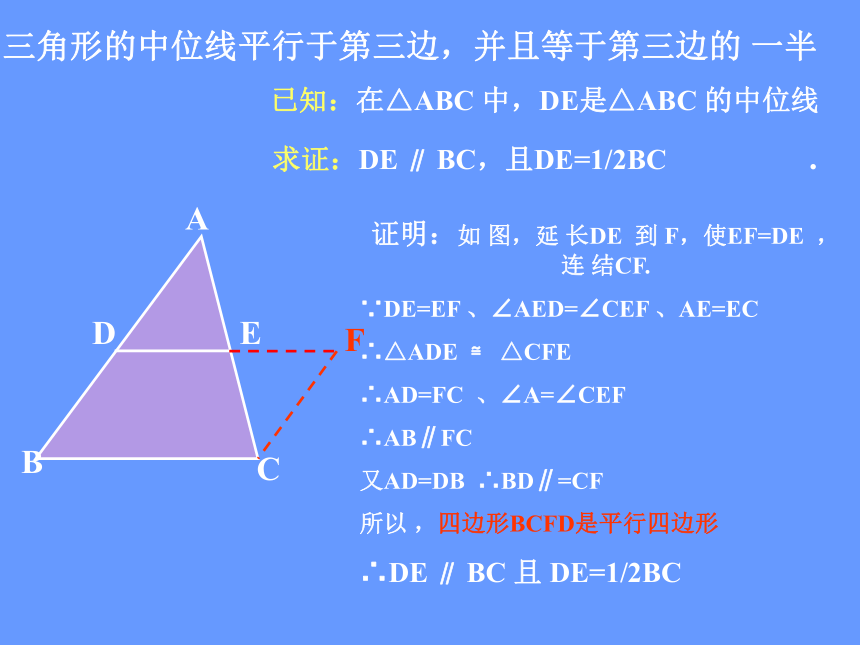
求证:DE ∥ BC,且DE=1/2BC . 证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠CEF
∴AB∥FC
又AD=DB ∴BD∥=CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
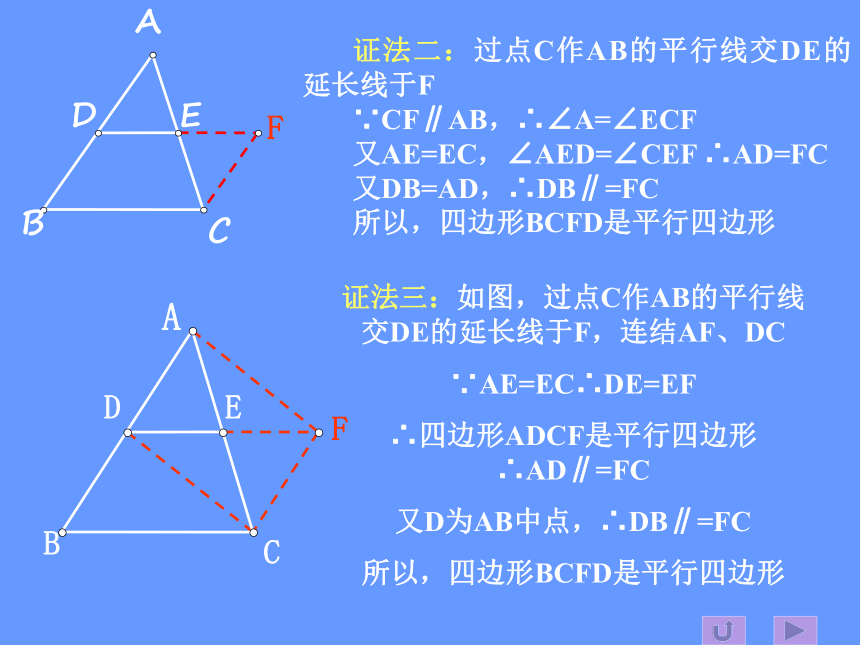
证法二:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,∴∠A=∠ECF
又AE=EC,∠AED=∠CEF ∴AD=FC
又DB=AD,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法三:如图,过点C作AB的平行线交DE的延长线于F,连结AF、DC
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形
?ABCEDFABCEDF证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
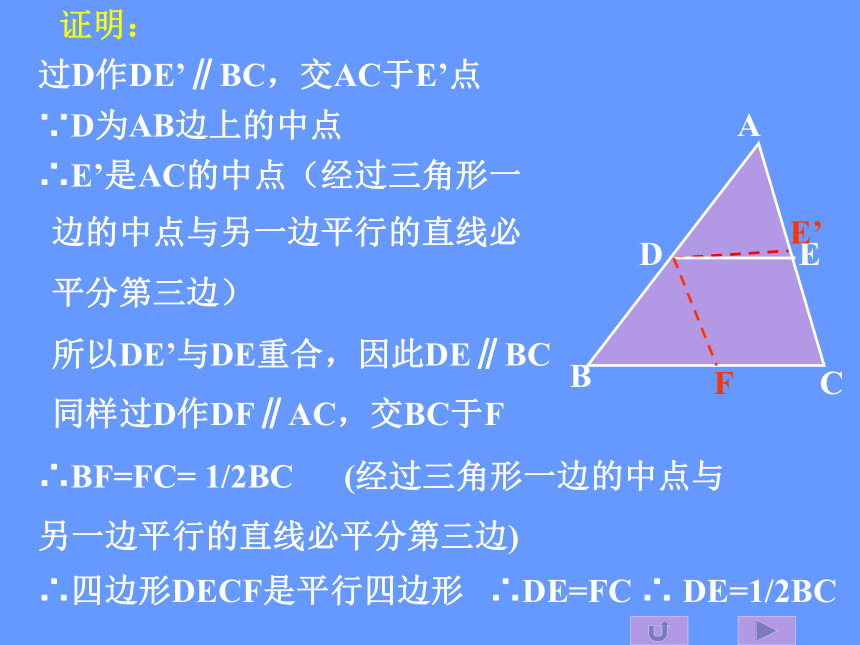
即DE=1/2BCABCEDFG过D作DE’∥BC,交AC于E’点∵D为AB边上的中点所以DE’与DE重合,因此DE∥BC同样过D作DF∥AC,交BC于F∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)∴四边形DECF是平行四边形∴DE=FC ∴ DE=1/2BCABCDEE’F证明:三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD。。EBACD 。。E。F5433. 梯形ABCD中AD∥BC,对角线AC、BD相交于点O,A’、
B’、C’、D’分别是AO、BO、CO、DO中点,则四边形A’B’C’D’是________若梯形ABCD周长为10,由四边形A’B’C’D’的周长为______
梯形5A 。。BC 。D。。
E4. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
2040随着学习的不断深入,同学们将会有更多的办法来解决这个问题例1例1.求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形 ⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是菱形,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是什么特殊四边形?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件? 2. 连结BD 证:EH ∥= FG 3.连结AC、BD ,证:EF∥HG, EH∥FG
4.连结AC、BD, 证:EF=HG, EH=FG 1.连结AC, 证:EF∥= HG如果四边形ABCD是特殊的四边形,将会有特殊的平行四边形EFGH出现吗?1. 如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则BC= ———34.592. 已知:如图 E、F把四边形ABCD的对角线BD三等分,CE、CF的延长线分别平分AB、AD .
求证:四边形ABCD是平行四边形 .ABDCEFGH已知:如图 E、F分别是AC、BD的中点,CD≧ AB,E、F不都是对角线的交点 .
求证: EF> 1/2(CD- AB) .图2G图3注意:在处理这些问题时,要求出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要作中点的连线或过中点作平行线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
⑶解决“中点问题”
三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:必做题:P184 页 4 、6 ; P180页 4
让学生自选一个顺次连结特殊四边形中点的问题,总结形成文字命题,并加以证明
把证明三角形中位线定理的几种方法整理出来
选做题:
作 业END①顺次连结平行四边形四边中点所得的四边形是————————②顺次连结等腰梯形四边中点所得的四边形是——————③顺次连结矩形四边中点所得的四边形是——————④顺次连结菱形四边中点所得的四边形是——————⑤顺次连结正方形四边中点所得的四边形是—————填空题:已知:梯形ABCD,AD∥BC,对角线AC、BD相交于点O, A’、B’、C’、D’分别是AO、BO、CO、DO的中 点,
求证:⑴四边形A’B’C’D’是梯形
⑵梯形ABCD的周长=梯形A’B’C’D’的周长的2倍ABCDOD’C’B’A’证明:⑴ ∵A’D’为△OAD的______
∴ A’D’ ___1/2AD 同理:B’C’ ∥=______
∵AD∥BC
∴A’D’ ___B’C’,由AD≠BC
∴ A’D’ ___B’C’
∴四边形A’B’C’D’是梯形
⑵ ∵_____为△OAD的中位线
∴AD=__A’D’ 同理:AB=_____
____=2B’C’, CD__2C’D’
∴AD+AB+BC+CD=
2(A’D’+A’B’+B’C’+C’D')
中位线∥=1/2BC∥≠A’D’22A’B’ BC=
E如图,在A、B外选一点C,连结AC和BC,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将教大家一种测量的方法。并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。三角形的中位线和三角形的中线
不同CBAFED定义:连接三角形两边中点的线段
叫做三角形的中位线
AF是△ABC的中线我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段 区分三角形的中位线和中线: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FE点是线段AC的中点
∵AD=DB且
DE∥BC
∴AE=EC ABCDE经过三角形一边的中点与另一边平行的直线必平分第三边.如图,已知,在△ABC中,点D为线段AB的中点,自D作DE ∥ BC,交AC于E,那么点E在AC的什么位置上? 为什么?这时DE是△ABC的___________中位线三角形的中位线平行于第三边,并且等于第三边的 一半ABCDEF已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC . 证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠CEF
∴AB∥FC
又AD=DB ∴BD∥=CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
证法二:过点C作AB的平行线交DE的延长线于F
∵CF∥AB,∴∠A=∠ECF
又AE=EC,∠AED=∠CEF ∴AD=FC
又DB=AD,∴DB∥=FC
所以,四边形BCFD是平行四边形
证法三:如图,过点C作AB的平行线交DE的延长线于F,连结AF、DC
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形
?ABCEDFABCEDF证法四:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC∴∠EAG=∠ECF
∴△AEG≌△CEF∴AG=FC,GE=EF
又AB∥GF,AG∥BF∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又D为AB中点,E为GF中点,∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BCABCEDFG过D作DE’∥BC,交AC于E’点∵D为AB边上的中点所以DE’与DE重合,因此DE∥BC同样过D作DF∥AC,交BC于F∴BF=FC= 1/2BC (经过三角形一边的中点与
另一边平行的直线必平分第三边)∴四边形DECF是平行四边形∴DE=FC ∴ DE=1/2BCABCDEE’F证明:三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD。。EBACD 。。E。F5433. 梯形ABCD中AD∥BC,对角线AC、BD相交于点O,A’、
B’、C’、D’分别是AO、BO、CO、DO中点,则四边形A’B’C’D’是________若梯形ABCD周长为10,由四边形A’B’C’D’的周长为______
梯形5A 。。BC 。D。。
E4. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
2040随着学习的不断深入,同学们将会有更多的办法来解决这个问题例1例1.求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形 ⑴在四边形ABCD另加条件AC=BD, 四边形EFGH是菱形,为什么?
⑵在四边形ABCD另加条件AC⊥BD,四边形EFGH是什么特殊四边形?为什么?
⑶若四边形EFGH是正方形,AC与BD应满足什么条件? 2. 连结BD 证:EH ∥= FG 3.连结AC、BD ,证:EF∥HG, EH∥FG
4.连结AC、BD, 证:EF=HG, EH=FG 1.连结AC, 证:EF∥= HG如果四边形ABCD是特殊的四边形,将会有特殊的平行四边形EFGH出现吗?1. 如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则BC= ———34.592. 已知:如图 E、F把四边形ABCD的对角线BD三等分,CE、CF的延长线分别平分AB、AD .
求证:四边形ABCD是平行四边形 .ABDCEFGH已知:如图 E、F分别是AC、BD的中点,CD≧ AB,E、F不都是对角线的交点 .
求证: EF> 1/2(CD- AB) .图2G图3注意:在处理这些问题时,要求出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要作中点的连线或过中点作平行线定 理 应 用:⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径
⑶解决“中点问题”
三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:必做题:P184 页 4 、6 ; P180页 4
让学生自选一个顺次连结特殊四边形中点的问题,总结形成文字命题,并加以证明
把证明三角形中位线定理的几种方法整理出来
选做题:
作 业END①顺次连结平行四边形四边中点所得的四边形是————————②顺次连结等腰梯形四边中点所得的四边形是——————③顺次连结矩形四边中点所得的四边形是——————④顺次连结菱形四边中点所得的四边形是——————⑤顺次连结正方形四边中点所得的四边形是—————填空题:已知:梯形ABCD,AD∥BC,对角线AC、BD相交于点O, A’、B’、C’、D’分别是AO、BO、CO、DO的中 点,
求证:⑴四边形A’B’C’D’是梯形
⑵梯形ABCD的周长=梯形A’B’C’D’的周长的2倍ABCDOD’C’B’A’证明:⑴ ∵A’D’为△OAD的______
∴ A’D’ ___1/2AD 同理:B’C’ ∥=______
∵AD∥BC
∴A’D’ ___B’C’,由AD≠BC
∴ A’D’ ___B’C’
∴四边形A’B’C’D’是梯形
⑵ ∵_____为△OAD的中位线
∴AD=__A’D’ 同理:AB=_____
____=2B’C’, CD__2C’D’
∴AD+AB+BC+CD=
2(A’D’+A’B’+B’C’+C’D')
中位线∥=1/2BC∥≠A’D’22A’B’ BC=
