2022-2023学年北师大版八年级数学下册 4.2提公因式法(第1课时)课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册 4.2提公因式法(第1课时)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 932.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 22:52:14 | ||
图片预览







文档简介
(共22张PPT)
主讲:XXX
4.2 提公因式法(第一课时)
北师大版八年级 下册
教学目标
素养目标
技能目标
知识目标
经历探索寻找多项式各项的公因式的过程,能确定多项式各项的公因式。
会用提公因式法进行因式分解。
由分解因数过渡到分解因式,进一步发展学生的类比思想。培养学生的初步归纳能力。
教学重难点
教学重点
教学难点
能准确地找出各项的公因式,并注意各种变形的符号问题.
能简单运用提公因式法进行因式分解.
创设情境 引入新课
思考1:
因式分解的概念
1. 因式分解:把一个多项式化成________________的形式,这种变形叫做把这个多项式因式分解.
几个整式的积
创设情境 引入新课
思考2:
整式乘法与因式分解之间的关系?
互为逆运算
创设情境 引入新课
计算:
解:
问:你是用什么方法计算的?这个式子的各项有相同的因数吗?
典例探究 深化新知
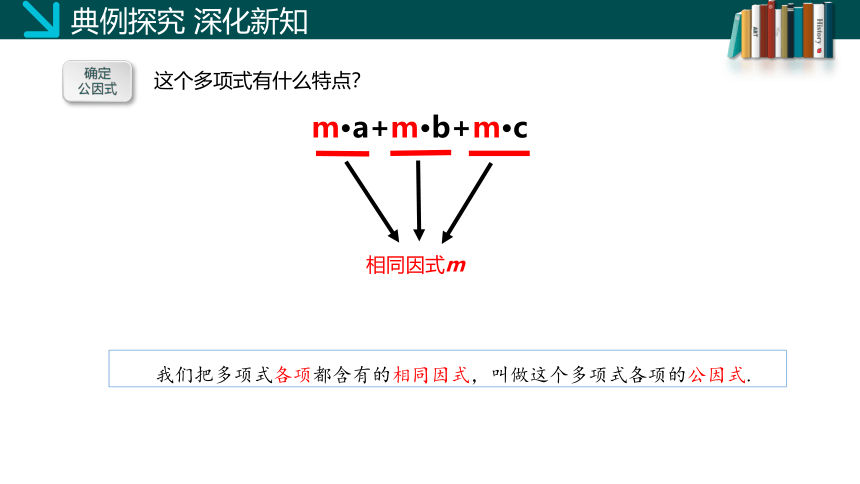
问题1:多项式ma+mb+mc有哪几项?
问题2:每一项的因式都分别有哪些?
问题3:这些项中有没有公共的因式,若有,公共的因
式是什么?
ma, mb, mc
依次为m, a和m, b和m, c
有,为m
典例探究 深化新知
确定
公因式
相同因式m
这个多项式有什么特点?
m a+m b+m c
我们把多项式各项都含有的相同因式,叫做这个多项式各项的公因式.
典例探究 深化新知
议一议
找 2 m 3 + 6 m 5 c 的公因式。
定系数
2
定字母
m
定指数
3
所以,这个多项式的公因式是 2 m 3
系数:公因式的系数是多项式各项系数的最大公约数;
字母:字母取多项式各项中都含有的相同的字母;
指数:相同字母的指数取各项中最小的一个,即字母最低次幂;
体验新知 学以致用
写出下列多项式的公因式.
(1)x-x2;
(2)abc+2a;
(3)abc-b2+2ab;
(4)a2+ax2;
x
a
b
a
做一做
归纳总结 认知升华
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
ma+ mb +mc
m
=
典例探究 深化新知
例1.
将下列各式分解因式:
(1) 3x+x3
解:原式 = x · 3 + x · x2
= x(3 + x2)
(2)7x3 - 21x2
解:原式 = 7x2 · x - 7x2 · 3
= 7x2(x-3)
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
典例探究 深化新知
例1.
将下列各式分解因式:
(3) 8a3b2 -12ab3c + ab
解:原式 = ab · 8a2b - ab · 12b2c + ab · 1
= ab(8a2b - 12b2c + 1)
当多项式的某一项和公因式相同时,提公因式后剩余的项是1。
典例探究 深化新知
例1.
将下列各式分解因式:
(4) – 24x3 –12x2 +28x
解:原式= - (24x3 + 12x2 - 28x)
= - (4x · 6x2 + 4x · 3x - 4x · 7)
= - 4x( 6x2 + 3x - 7)
当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.
典例探究 深化新知
例2.
小明的解法有误吗?
错误。公因式没有提尽,还可以提出公因式2
因式分解:12x2y+18xy2.
解:原式 =3xy(4x + 6y).
注意:公因式要提尽.
正确解:原式=6xy(2x+3y).
体验新知 学以致用
做一做
将下列各式分解因式:
(1) ma + mb;
(2) 5y3 + 20y2;
(3) 4m3 - 6m2;
(4) a2b – 5ab+9b;
(5) -a2 +ab - ac;
(6) -2x3 +4x2 – 6x.
解:原式= m(a+b);
解:原式= 5y2(y+4);
解:原式= 2m2(2m-3);
解:原式= b(a2-5a+9);
解:原式= -a(a-b+c);
解:原式= -2x(x2-2x+3).
体验新知 学以致用
做一做
分析:(1)题每一项都含有公因数978,把978作为公因式提出;
(2)题先对所求式提取公因式,再整体代入计算.
利用提公因式法解答下列各题:
(1)计算:978×85+978×7+978×8;
(2)已知2x-y=3 ,xy=2,求2x4y3-x3y4的值.
解:(1)原式=978×(85+7+8)=978×100=97 800.
(2)2x4y3-x3y4=x3y3(2x-y)=(xy)3(2x-y).
当2x-y=3 ,xy=2时,原式=23×3=24
归纳总结 认知升华
思想方法
逆向思维,转化思维。
确定公因式
定系数:公因式的系数是多项式各项系数的最大公约数.(当系数是整数时)
定字母:字母取多项式各项中都含有的相同的字母.
定指数:相同字母的指数取各项中字母的最低次幂.
提公因式法
第一步:找出公因式;
第二步:提公因式(把多项式化为两个因式的乘积)
巩固练习 拓展提高
1.因式分解:x2-2x+(x-2)=_____________.
(x+1)(x-2)
巩固练习 拓展提高
2.已知x2+3x-2=0,则2x3+6x2-4x=_______.
3.若ab=2,a-b=-1,则代数式a2b-ab2的值等于________.
0
-2
布置作业 减负增效
习题4.2第1、2题
青春由磨砺而出彩,
人生因奋斗而升华!
主讲:XXX
主讲:XXX
4.2 提公因式法(第一课时)
北师大版八年级 下册
教学目标
素养目标
技能目标
知识目标
经历探索寻找多项式各项的公因式的过程,能确定多项式各项的公因式。
会用提公因式法进行因式分解。
由分解因数过渡到分解因式,进一步发展学生的类比思想。培养学生的初步归纳能力。
教学重难点
教学重点
教学难点
能准确地找出各项的公因式,并注意各种变形的符号问题.
能简单运用提公因式法进行因式分解.
创设情境 引入新课
思考1:
因式分解的概念
1. 因式分解:把一个多项式化成________________的形式,这种变形叫做把这个多项式因式分解.
几个整式的积
创设情境 引入新课
思考2:
整式乘法与因式分解之间的关系?
互为逆运算
创设情境 引入新课
计算:
解:
问:你是用什么方法计算的?这个式子的各项有相同的因数吗?
典例探究 深化新知
问题1:多项式ma+mb+mc有哪几项?
问题2:每一项的因式都分别有哪些?
问题3:这些项中有没有公共的因式,若有,公共的因
式是什么?
ma, mb, mc
依次为m, a和m, b和m, c
有,为m
典例探究 深化新知
确定
公因式
相同因式m
这个多项式有什么特点?
m a+m b+m c
我们把多项式各项都含有的相同因式,叫做这个多项式各项的公因式.
典例探究 深化新知
议一议
找 2 m 3 + 6 m 5 c 的公因式。
定系数
2
定字母
m
定指数
3
所以,这个多项式的公因式是 2 m 3
系数:公因式的系数是多项式各项系数的最大公约数;
字母:字母取多项式各项中都含有的相同的字母;
指数:相同字母的指数取各项中最小的一个,即字母最低次幂;
体验新知 学以致用
写出下列多项式的公因式.
(1)x-x2;
(2)abc+2a;
(3)abc-b2+2ab;
(4)a2+ax2;
x
a
b
a
做一做
归纳总结 认知升华
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
ma+ mb +mc
m
=
典例探究 深化新知
例1.
将下列各式分解因式:
(1) 3x+x3
解:原式 = x · 3 + x · x2
= x(3 + x2)
(2)7x3 - 21x2
解:原式 = 7x2 · x - 7x2 · 3
= 7x2(x-3)
分析:提公因式法步骤(分两步)
第一步:找出公因式;
第二步:提取公因式 ,即将多项式化为两个因式的乘积.
典例探究 深化新知
例1.
将下列各式分解因式:
(3) 8a3b2 -12ab3c + ab
解:原式 = ab · 8a2b - ab · 12b2c + ab · 1
= ab(8a2b - 12b2c + 1)
当多项式的某一项和公因式相同时,提公因式后剩余的项是1。
典例探究 深化新知
例1.
将下列各式分解因式:
(4) – 24x3 –12x2 +28x
解:原式= - (24x3 + 12x2 - 28x)
= - (4x · 6x2 + 4x · 3x - 4x · 7)
= - 4x( 6x2 + 3x - 7)
当多项式第一项系数是负数,通常先提出“-”号,使括号内第一项系数变为正数,注意括号内各项都要变号.
典例探究 深化新知
例2.
小明的解法有误吗?
错误。公因式没有提尽,还可以提出公因式2
因式分解:12x2y+18xy2.
解:原式 =3xy(4x + 6y).
注意:公因式要提尽.
正确解:原式=6xy(2x+3y).
体验新知 学以致用
做一做
将下列各式分解因式:
(1) ma + mb;
(2) 5y3 + 20y2;
(3) 4m3 - 6m2;
(4) a2b – 5ab+9b;
(5) -a2 +ab - ac;
(6) -2x3 +4x2 – 6x.
解:原式= m(a+b);
解:原式= 5y2(y+4);
解:原式= 2m2(2m-3);
解:原式= b(a2-5a+9);
解:原式= -a(a-b+c);
解:原式= -2x(x2-2x+3).
体验新知 学以致用
做一做
分析:(1)题每一项都含有公因数978,把978作为公因式提出;
(2)题先对所求式提取公因式,再整体代入计算.
利用提公因式法解答下列各题:
(1)计算:978×85+978×7+978×8;
(2)已知2x-y=3 ,xy=2,求2x4y3-x3y4的值.
解:(1)原式=978×(85+7+8)=978×100=97 800.
(2)2x4y3-x3y4=x3y3(2x-y)=(xy)3(2x-y).
当2x-y=3 ,xy=2时,原式=23×3=24
归纳总结 认知升华
思想方法
逆向思维,转化思维。
确定公因式
定系数:公因式的系数是多项式各项系数的最大公约数.(当系数是整数时)
定字母:字母取多项式各项中都含有的相同的字母.
定指数:相同字母的指数取各项中字母的最低次幂.
提公因式法
第一步:找出公因式;
第二步:提公因式(把多项式化为两个因式的乘积)
巩固练习 拓展提高
1.因式分解:x2-2x+(x-2)=_____________.
(x+1)(x-2)
巩固练习 拓展提高
2.已知x2+3x-2=0,则2x3+6x2-4x=_______.
3.若ab=2,a-b=-1,则代数式a2b-ab2的值等于________.
0
-2
布置作业 减负增效
习题4.2第1、2题
青春由磨砺而出彩,
人生因奋斗而升华!
主讲:XXX
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
