三角形的中位线(1[下学期]
图片预览

文档简介
三角形的中位线(一)
一、教学目的和要求
使学生了解三角形中位线的定义,掌握三角形中位线性质定理的证明和应用。
通过定理的证明进一步培养学生的逻辑推理能力。
二、教学重点和难点
重点:掌握三角形中位线定义,及性质定理的证明。
难点:证题中正确添加辅助线。
三、教学过程
(一)复习、引入
提问:
1、平行线等分线段定理的内容
2、叙述定理的两个推论(画图示意)
练习:见图1
AD是中BC边上的中线,E为AD的中点,连结BE并延长交AC于F,若AF=2,求AC的长。
A
F
E
M
B D C
图1
过D点作BF的平行线交AC于M,因为BD=DC,AE=ED,利用平行线等分线段定理推论2,可得AF=FM=MC,所以AC=6。
如果我们将平行线等分线段定理推论2的条件、结论交换一下,是否成立?
已知:D、E是中AB、AC边的中点,则DE//BC。这就是我们今天将要研究的课题。
(二)新课
定义:连结三角形两边中点的线段叫做三角形的中位线。
DE叫做的中位线。
注意:
1. 中位线是线段,它的端点是三角形两边的中点。
2. 中位线与中线都是三角形的重要线段,它们端点位置不同,是两个不同的概念。
每个三角形有三条中位线。
下面我们研究三角形的中位线与第三边的数量及位置关系。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
已知:如图2,中,AD=DB,AE=EC
求证:
A
D 1 E F
2
B C
图2
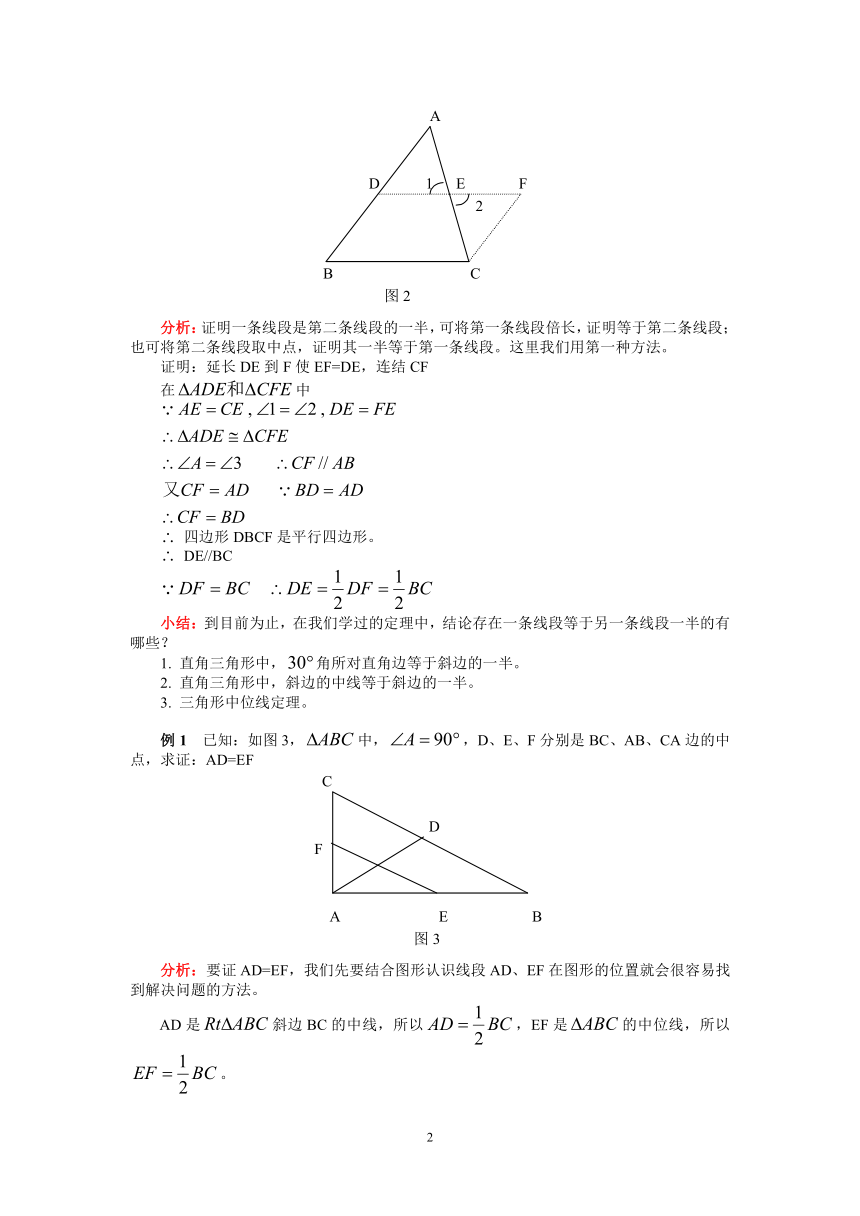
分析:证明一条线段是第二条线段的一半,可将第一条线段倍长,证明等于第二条线段;也可将第二条线段取中点,证明其一半等于第一条线段。这里我们用第一种方法。
证明:延长DE到F使EF=DE,连结CF
在中
四边形DBCF是平行四边形。
DE//BC
小结:到目前为止,在我们学过的定理中,结论存在一条线段等于另一条线段一半的有哪些?
1. 直角三角形中,角所对直角边等于斜边的一半。
2. 直角三角形中,斜边的中线等于斜边的一半。
3. 三角形中位线定理。
例1 已知:如图3,中,,D、E、F分别是BC、AB、CA边的中点,求证:AD=EF
C
D
F
A E B
图3
分析:要证AD=EF,我们先要结合图形认识线段AD、EF在图形的位置就会很容易找到解决问题的方法。
AD是斜边BC的中线,所以,EF是的中位线,所以。
证明:
分别是AB、AC的中点
例2 求证:顺次连结矩形四边中点所得的四边形是菱形。
已知:矩形ABCD中,H、E、F、G分别是四边AB、BC、CD、AD的中点,求证:四边形HEFG是菱形。
A G D
H F
B E C
图4
分析:判定菱形,可以用一组邻边相等的平行四边形;四边相等的四边形……。
分析题目条件中,由于中点条件较多,联想到三角形中位线定理,利用对角线将矩形分割成三角形,则得到所证四边形各边均等于对角线的一半,而矩形的对角线相等。
证明:连结AC、BD。
此题还可以用全等三角形证明四边相等,但不如利用三角形中位线简便。
例3 已知:如图139,正方形ABCD中,AC、BD交于O点,的平分线交AC于E,交DC于F。
A D
O
F
3 4 E
1 G
2
B C
图5
求证:
分析:观察图形,在中,DF是底边,O是BD的中点,如果E也是BF中点,那么可得。但是显然E不是BF中点,所以我们要做出这个三角形的中位线,再证明OE就等于中位线长。作OG//DF,那么。只需证OG=OE。
证明:过点O作OG//DC,交BF于G
在正方形ABCD中,
此题还可以把OE看成是三角形的中位线,作出三角形的底边,再证DF等于三角形的底边。即过D点作AC的平行线交BF的延长线于H,则,只需证DF=DH即可。
(三)巩固练习
1. 已知顺次连结三角形各边中点所成三角形的周长是10cm,求原三角形的周长。(20cm)
2. 求证:任意四边形一组对边中点的线段,小于两条对角线和的一半。
已知:如图140,四边形ABCD中,M,N分别为AD、BC边的中点。
A M
D
E
B N C
图6
证明:取AB的中点E,连结EM、EN
(四)小结
今天所讲的三角形中位线定理很重要,它的应用广泛且灵活。添加辅助线要根据图形具体分析,可以过三角形的一边中点作底边的平行线;若有两个或两个以上中点时,连结边的端点构造成三角形的中位线的形式。
(五)作业
1. 已知三角形三边之比为3:4:5,且周长为60cm,连结三边中点,求所得三角形各边长。
2. 已知,在四边形ABCD中,对边AD=BC,P是对角线BD的中点,M、N分别是DC、AB的中点。求证:。
3. 在中,于D,E、F、G分别是AC、AB、BC的中点。求证:四边形DEFG是等腰梯形。
4. 四边形ABCD两条对角线AC、BD相等,M、N为一组对边的中点,MN交BD于E、交AC于F,两对角线交于O。
求证:是等腰三角形。
5
一、教学目的和要求
使学生了解三角形中位线的定义,掌握三角形中位线性质定理的证明和应用。
通过定理的证明进一步培养学生的逻辑推理能力。
二、教学重点和难点
重点:掌握三角形中位线定义,及性质定理的证明。
难点:证题中正确添加辅助线。
三、教学过程
(一)复习、引入
提问:
1、平行线等分线段定理的内容
2、叙述定理的两个推论(画图示意)
练习:见图1
AD是中BC边上的中线,E为AD的中点,连结BE并延长交AC于F,若AF=2,求AC的长。
A
F
E
M
B D C
图1
过D点作BF的平行线交AC于M,因为BD=DC,AE=ED,利用平行线等分线段定理推论2,可得AF=FM=MC,所以AC=6。
如果我们将平行线等分线段定理推论2的条件、结论交换一下,是否成立?
已知:D、E是中AB、AC边的中点,则DE//BC。这就是我们今天将要研究的课题。
(二)新课
定义:连结三角形两边中点的线段叫做三角形的中位线。
DE叫做的中位线。
注意:
1. 中位线是线段,它的端点是三角形两边的中点。
2. 中位线与中线都是三角形的重要线段,它们端点位置不同,是两个不同的概念。
每个三角形有三条中位线。
下面我们研究三角形的中位线与第三边的数量及位置关系。
三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半。
已知:如图2,中,AD=DB,AE=EC
求证:
A
D 1 E F
2
B C
图2
分析:证明一条线段是第二条线段的一半,可将第一条线段倍长,证明等于第二条线段;也可将第二条线段取中点,证明其一半等于第一条线段。这里我们用第一种方法。
证明:延长DE到F使EF=DE,连结CF
在中
四边形DBCF是平行四边形。
DE//BC
小结:到目前为止,在我们学过的定理中,结论存在一条线段等于另一条线段一半的有哪些?
1. 直角三角形中,角所对直角边等于斜边的一半。
2. 直角三角形中,斜边的中线等于斜边的一半。
3. 三角形中位线定理。
例1 已知:如图3,中,,D、E、F分别是BC、AB、CA边的中点,求证:AD=EF
C
D
F
A E B
图3
分析:要证AD=EF,我们先要结合图形认识线段AD、EF在图形的位置就会很容易找到解决问题的方法。
AD是斜边BC的中线,所以,EF是的中位线,所以。
证明:
分别是AB、AC的中点
例2 求证:顺次连结矩形四边中点所得的四边形是菱形。
已知:矩形ABCD中,H、E、F、G分别是四边AB、BC、CD、AD的中点,求证:四边形HEFG是菱形。
A G D
H F
B E C
图4
分析:判定菱形,可以用一组邻边相等的平行四边形;四边相等的四边形……。
分析题目条件中,由于中点条件较多,联想到三角形中位线定理,利用对角线将矩形分割成三角形,则得到所证四边形各边均等于对角线的一半,而矩形的对角线相等。
证明:连结AC、BD。
此题还可以用全等三角形证明四边相等,但不如利用三角形中位线简便。
例3 已知:如图139,正方形ABCD中,AC、BD交于O点,的平分线交AC于E,交DC于F。
A D
O
F
3 4 E
1 G
2
B C
图5
求证:
分析:观察图形,在中,DF是底边,O是BD的中点,如果E也是BF中点,那么可得。但是显然E不是BF中点,所以我们要做出这个三角形的中位线,再证明OE就等于中位线长。作OG//DF,那么。只需证OG=OE。
证明:过点O作OG//DC,交BF于G
在正方形ABCD中,
此题还可以把OE看成是三角形的中位线,作出三角形的底边,再证DF等于三角形的底边。即过D点作AC的平行线交BF的延长线于H,则,只需证DF=DH即可。
(三)巩固练习
1. 已知顺次连结三角形各边中点所成三角形的周长是10cm,求原三角形的周长。(20cm)
2. 求证:任意四边形一组对边中点的线段,小于两条对角线和的一半。
已知:如图140,四边形ABCD中,M,N分别为AD、BC边的中点。
A M
D
E
B N C
图6
证明:取AB的中点E,连结EM、EN
(四)小结
今天所讲的三角形中位线定理很重要,它的应用广泛且灵活。添加辅助线要根据图形具体分析,可以过三角形的一边中点作底边的平行线;若有两个或两个以上中点时,连结边的端点构造成三角形的中位线的形式。
(五)作业
1. 已知三角形三边之比为3:4:5,且周长为60cm,连结三边中点,求所得三角形各边长。
2. 已知,在四边形ABCD中,对边AD=BC,P是对角线BD的中点,M、N分别是DC、AB的中点。求证:。
3. 在中,于D,E、F、G分别是AC、AB、BC的中点。求证:四边形DEFG是等腰梯形。
4. 四边形ABCD两条对角线AC、BD相等,M、N为一组对边的中点,MN交BD于E、交AC于F,两对角线交于O。
求证:是等腰三角形。
5
