【2023中考二轮复习】角的存在性问题专题探究(含答案)
文档属性
| 名称 | 【2023中考二轮复习】角的存在性问题专题探究(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 10:31:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023年 中考存在性问题—— 角的存在性问题专题探究
角的存在性问题作为压轴题目,结合了“分类讨论思想”,“方程思想”“三角函数”,势必要比单纯的菱形判定思考难度要大得多,因此我在研究了近些年中考真题之后尝试性地总结一下角存在性问题的通用解法,以供大家参考.
解题攻略
【基本概念】
角相等问题在坐标系中可以由以下几种方式得到:
等腰三角形两底角相等;
平行线的性质;
相似三角形对应角相等;
等角三角函数相等。
2.【基本题型】
(1)已知等角求坐标
(2)构造等角求坐标
3.【解题思路】
类型一:将等角问题转化成等腰三角形或平行线问题。
类型二:将等角问题转化成等角所在三角形相似或等角对应的三角函数(通常是正切值)相等问题。这类问题有两种情况:一种是所求角的一边与坐标轴平行(重合);另一种是所求角的边不与坐标轴平行。
典例剖析
类型一:已知等角,求点的坐标
当题目中出现相等的角时,可以通过计算已知角的三角比,用所求点的横纵坐标表示另一角的三角比,从而建立等量关系;同时也可以通过构造相似三角形,利用比例线段解决问题。
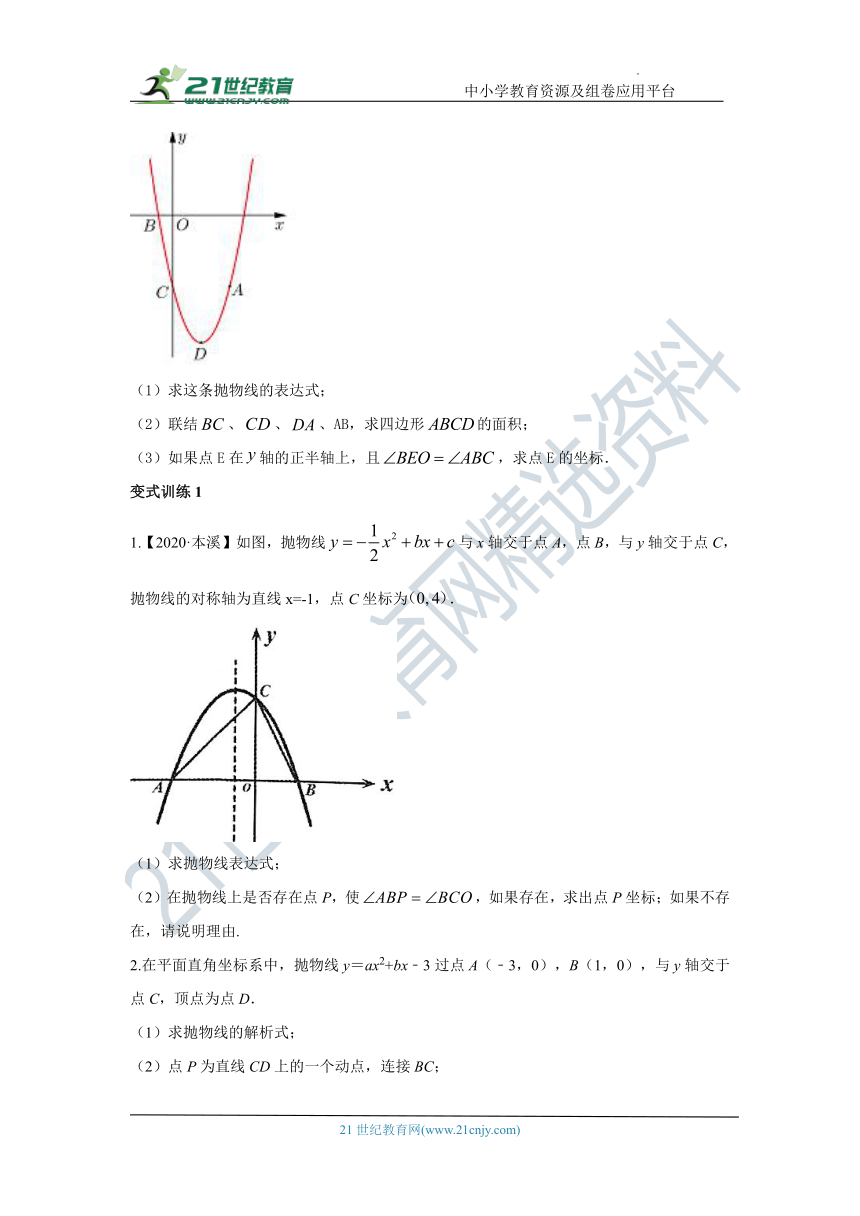
例1.如图,抛物线()经过点,与轴的负半轴交于点,与轴交于点,且,抛物线的顶点为.
(1)求这条抛物线的表达式;
(2)联结、、、AB,求四边形的面积;
(3)如果点E在轴的正半轴上,且,求点E的坐标.
变式训练1
1.【2020·本溪】如图,抛物线与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线x=-1,点C坐标为.
(1)求抛物线表达式;
(2)在抛物线上是否存在点P,使,如果存在,求出点P坐标;如果不存在,请说明理由.
2.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
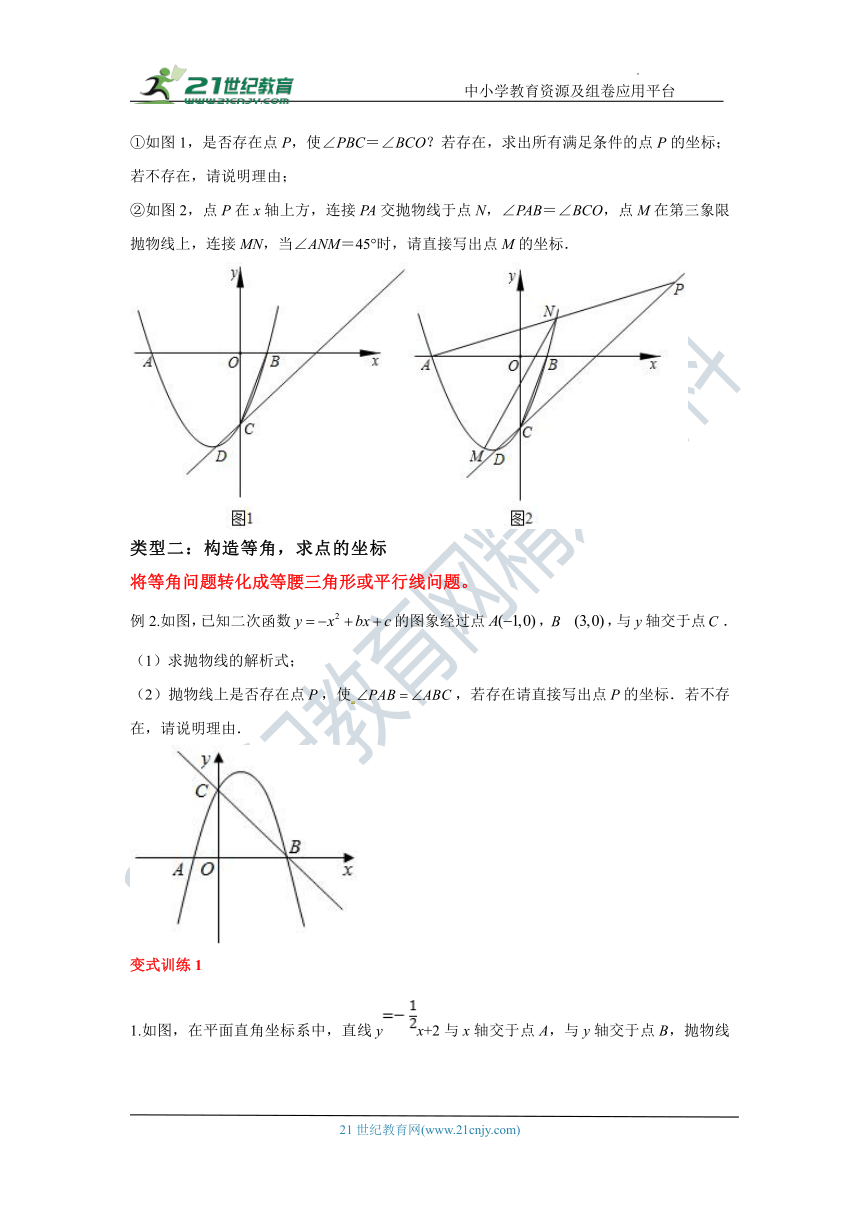
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
类型二:构造等角,求点的坐标
将等角问题转化成等腰三角形或平行线问题。
例2.如图,已知二次函数的图象经过点, ,与轴交于点.
(1)求抛物线的解析式;
(2)抛物线上是否存在点,使,若存在请直接写出点的坐标.若不存在,请说明理由.
变式训练1
1.如图,在平面直角坐标系中,直线yx+2与x轴交于点A,与y轴交于点B,抛物线yx2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
中考冲刺
1:抛物线y=-x+3x+4,与坐标轴交于点A、B、C,CP⊥y轴交抛物线与点P,点M为A、C间抛物线上一点(包括端点),求满足∠MPO=∠POA的点M的坐标。
分析:显然符合条件的点M有两个,OP上方一个,OP下方一个、当M在OP上方时,由∠MPO=∠POA可知PM//OA,则M与C点重合。当M在OP下方时,∠MPO=∠POA,这两角组成的三角形是等腰三角形。设PM与x轴交于点D,坐标为D(n,0),由两点间距离公式可表示出OD、PD长,根据OD=PD列方程即可求出D点坐标,再求出PD直线表达式与抛物线表达式联立,进而求出M点坐标。
2.如图,在平面直角坐标系中,直线 y=x+2与x轴交于点A,与y轴交于点C,抛物线y=-x+bx+c 经过A,C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
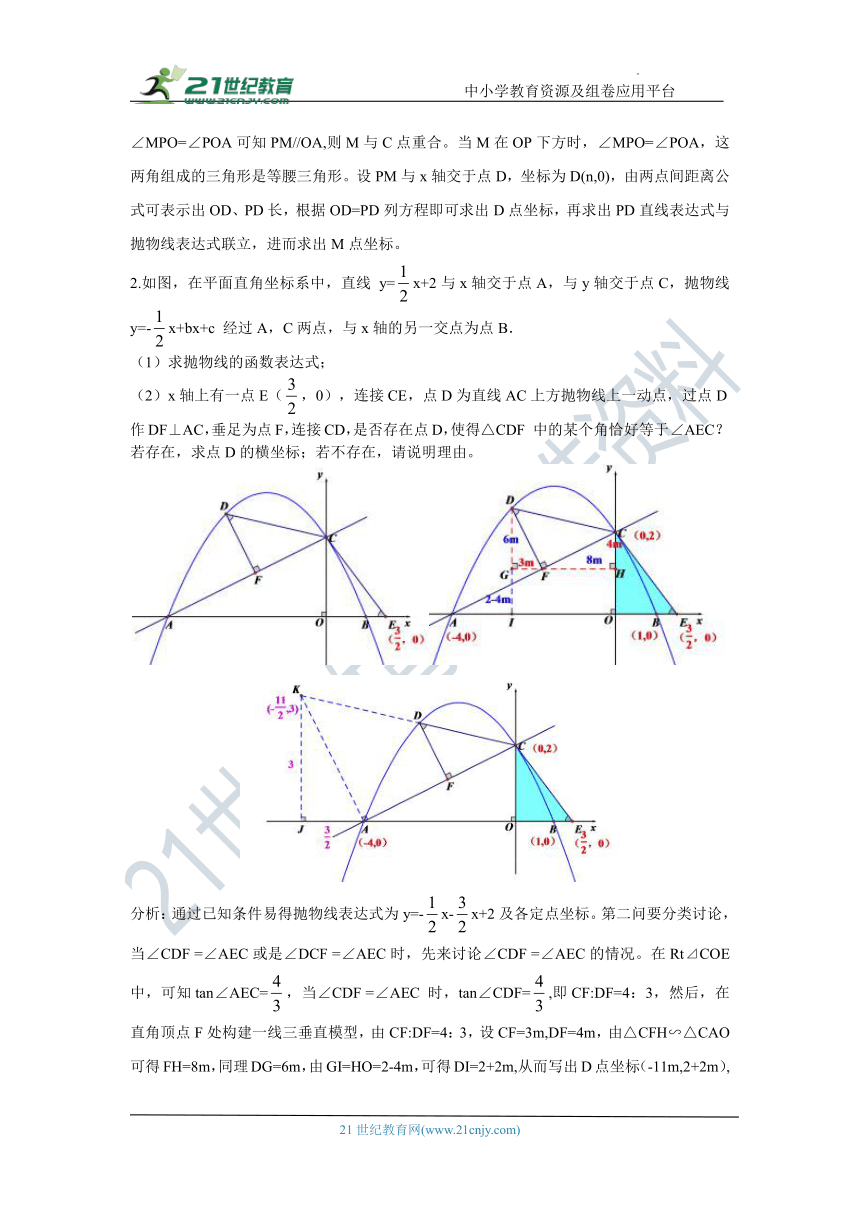
(2)x轴上有一点E(,0),连接CE,点D为直线AC上方抛物线上一动点,过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF 中的某个角恰好等于∠AEC?若存在,求点D的横坐标;若不存在,请说明理由。
分析:通过已知条件易得抛物线表达式为y=-x-x+2及各定点坐标。第二问要分类讨论,当∠CDF =∠AEC或是∠DCF =∠AEC时,先来讨论∠CDF =∠AEC的情况。在Rt⊿COE中,可知tan∠AEC=,当∠CDF =∠AEC 时,tan∠CDF=,即CF:DF=4:3,然后,在直角顶点F处构建一线三垂直模型,由CF:DF=4:3,设CF=3m,DF=4m,由△CFH∽△CAO可得FH=8m,同理DG=6m,由GI=HO=2-4m,可得DI=2+2m,从而写出D点坐标(-11m,2+2m),将其代入抛物线表达式求得D点坐标。
或是在A处作垂直构建一线三垂直模型,利用相似写出K点坐标,在求出CK直线表达式与抛物线表达式联立从而求出交点D 的坐标。
当∠DCF =∠AEC 时,可用同样方法求出D点坐标。
综合上面题目,对于二次函数中的角相等问题,首选方法是利用等角的三角比解决问题(利用一线三等角模型或者拆分特殊角来发现等角),其次选择利用相似三角形中的比例线段解决问题。
二次函数中的角相等问题比较灵活,同学们在遇到具体问题时具体分析,合理构造等角,解决问题。
答案解析
例1.【答案】(1);(2)18;(3).
【分析】(1)先求出C、B的坐标,代入抛物线的解析式即可得到结论;
(2)求出D的坐标,由计算即可;
(3)过点作,垂足为点,由△ABC的面积求出CH的长,在Rt△BCH中,求出tan∠CBH,在Rt△BOE中,根据tan∠BEO,即可得出E的坐标.
【详解】(1)∵抛物线与轴交于点,,∴.∵,∴.又点在轴的负半轴上,∴.
∵抛物线经过点和点,
∴,解得,
∴这条抛物线的表达式为;
(2)由,得顶点的坐标是.联结,
∵点的坐标是,点的坐标是,又,,∴;
(3)过点作,垂足为点.∵,,
∴.在Rt中,,,,∴;
在Rt中,,.
∵,∴,得,
∴点的坐标为.
考点:二次函数的图象,二元一次方程组,三角函数,三角形的面积.
变式训练1
1.【答案】见解析.
【解析】解:(1)∵抛物线对称轴为x=-1
即
∴b=-1
将(0,4)代入中,得c=4,
∴
(2)过P作轴于点E
易证得△PEB∽△BOC,
∴
设,则
①当点P在x轴上方时:
解得(舍)
②当点P在x轴下方时:
解得(舍)
综上所述,或.
2.【答案】见解析.
【解析】解:(1)y=ax2+bx﹣3=a(x+3)(x﹣1),
解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3;
(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),
由点C、D的坐标知,直线CD的表达式为:y=x﹣3;
tan∠BCO,则cos∠BCO;
①当点P(P′)在点C的右侧时,
∵∠PAB=∠BCO,
故P′B∥y轴,则点P′(1,﹣2);
当点P在点C的左侧时,
设直线PB交y轴于点H,过点H作HN⊥BC于点N,
∵∠PAB=∠BCO,
∴△BCH为等腰三角形, BC=2CH cos∠BCO=2×CH,
解得:CH,则OH=3﹣CH,故点H(0,),
由点B、H的坐标得,直线BH的表达式为:yx,
联立yx,y=x2+2x﹣3,解得:,
所以点P的坐标为(1,﹣2)或(﹣5,﹣8);
②∵∠PAB=∠BCO,而tan∠BCO,
故设直线AP的表达式为:yx+s,将点A的坐标代入上式并解得:s=1,
故直线AP的表达式为:yx+1,
联立①③并解得:,故点N(,);
设△AMN的外接圆为圆R,
当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),
∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,
∴∠RMH=∠GAR,
∵AR=MR,∠AGR=∠RHM=90°,
∴△AGR≌△RHM(AAS),
∴AG=m+3=RH,RG=﹣n=MH,
∴点M(m+n,n﹣m﹣3),
将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3,
由题意得:AR=NR,即(m+3)2=(m)2+()2,解得:,
故点M(,).
例2.【答案】见解析.
【解析】解:(1)根据题意得,
解得.
故抛物线的解析式为;
(2)二次函数的对称轴是x=1,
当x=0时,y=3,
则C(0,3),
点C关于对称轴的对应点,
设直线BC的解析式为y=kx+3,
则k=-1.
则直线BC的解析式为,
设与BC平行的直线AP的解析式为,
则,
解得.
则与平行的直线的解析式为,
联立,
解得,(舍去).
即P(4,-5).
综上所述,P(2,3)、(4,-5).
变式训练2
1.【答案】见解析.
【解析】解:(1)直线yx+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
所以抛物线的表达式为:yx2x+2;
(2)作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
由点A、B′的坐标得,直线AB′的表达式为:yx﹣2,
联立yx2x+2,yx﹣2,解得:x=3或﹣2,
故点P的坐标为(3,)或(﹣2,﹣3);
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:mn2n;
②mn2n,
∵0,故m有最大值,当n时,m的最大值为,
而m>0,
故0<m时,符合条件的N点的个数有2个.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023年 中考存在性问题—— 角的存在性问题专题探究
角的存在性问题作为压轴题目,结合了“分类讨论思想”,“方程思想”“三角函数”,势必要比单纯的菱形判定思考难度要大得多,因此我在研究了近些年中考真题之后尝试性地总结一下角存在性问题的通用解法,以供大家参考.
解题攻略
【基本概念】
角相等问题在坐标系中可以由以下几种方式得到:
等腰三角形两底角相等;
平行线的性质;
相似三角形对应角相等;
等角三角函数相等。
2.【基本题型】
(1)已知等角求坐标
(2)构造等角求坐标
3.【解题思路】
类型一:将等角问题转化成等腰三角形或平行线问题。
类型二:将等角问题转化成等角所在三角形相似或等角对应的三角函数(通常是正切值)相等问题。这类问题有两种情况:一种是所求角的一边与坐标轴平行(重合);另一种是所求角的边不与坐标轴平行。
典例剖析
类型一:已知等角,求点的坐标
当题目中出现相等的角时,可以通过计算已知角的三角比,用所求点的横纵坐标表示另一角的三角比,从而建立等量关系;同时也可以通过构造相似三角形,利用比例线段解决问题。
例1.如图,抛物线()经过点,与轴的负半轴交于点,与轴交于点,且,抛物线的顶点为.
(1)求这条抛物线的表达式;
(2)联结、、、AB,求四边形的面积;
(3)如果点E在轴的正半轴上,且,求点E的坐标.
变式训练1
1.【2020·本溪】如图,抛物线与x轴交于点A,点B,与y轴交于点C,抛物线的对称轴为直线x=-1,点C坐标为.
(1)求抛物线表达式;
(2)在抛物线上是否存在点P,使,如果存在,求出点P坐标;如果不存在,请说明理由.
2.在平面直角坐标系中,抛物线y=ax2+bx﹣3过点A(﹣3,0),B(1,0),与y轴交于点C,顶点为点D.
(1)求抛物线的解析式;
(2)点P为直线CD上的一个动点,连接BC;
①如图1,是否存在点P,使∠PBC=∠BCO?若存在,求出所有满足条件的点P的坐标;若不存在,请说明理由;
②如图2,点P在x轴上方,连接PA交抛物线于点N,∠PAB=∠BCO,点M在第三象限抛物线上,连接MN,当∠ANM=45°时,请直接写出点M的坐标.
类型二:构造等角,求点的坐标
将等角问题转化成等腰三角形或平行线问题。
例2.如图,已知二次函数的图象经过点, ,与轴交于点.
(1)求抛物线的解析式;
(2)抛物线上是否存在点,使,若存在请直接写出点的坐标.若不存在,请说明理由.
变式训练1
1.如图,在平面直角坐标系中,直线yx+2与x轴交于点A,与y轴交于点B,抛物线yx2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
中考冲刺
1:抛物线y=-x+3x+4,与坐标轴交于点A、B、C,CP⊥y轴交抛物线与点P,点M为A、C间抛物线上一点(包括端点),求满足∠MPO=∠POA的点M的坐标。
分析:显然符合条件的点M有两个,OP上方一个,OP下方一个、当M在OP上方时,由∠MPO=∠POA可知PM//OA,则M与C点重合。当M在OP下方时,∠MPO=∠POA,这两角组成的三角形是等腰三角形。设PM与x轴交于点D,坐标为D(n,0),由两点间距离公式可表示出OD、PD长,根据OD=PD列方程即可求出D点坐标,再求出PD直线表达式与抛物线表达式联立,进而求出M点坐标。
2.如图,在平面直角坐标系中,直线 y=x+2与x轴交于点A,与y轴交于点C,抛物线y=-x+bx+c 经过A,C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)x轴上有一点E(,0),连接CE,点D为直线AC上方抛物线上一动点,过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF 中的某个角恰好等于∠AEC?若存在,求点D的横坐标;若不存在,请说明理由。
分析:通过已知条件易得抛物线表达式为y=-x-x+2及各定点坐标。第二问要分类讨论,当∠CDF =∠AEC或是∠DCF =∠AEC时,先来讨论∠CDF =∠AEC的情况。在Rt⊿COE中,可知tan∠AEC=,当∠CDF =∠AEC 时,tan∠CDF=,即CF:DF=4:3,然后,在直角顶点F处构建一线三垂直模型,由CF:DF=4:3,设CF=3m,DF=4m,由△CFH∽△CAO可得FH=8m,同理DG=6m,由GI=HO=2-4m,可得DI=2+2m,从而写出D点坐标(-11m,2+2m),将其代入抛物线表达式求得D点坐标。
或是在A处作垂直构建一线三垂直模型,利用相似写出K点坐标,在求出CK直线表达式与抛物线表达式联立从而求出交点D 的坐标。
当∠DCF =∠AEC 时,可用同样方法求出D点坐标。
综合上面题目,对于二次函数中的角相等问题,首选方法是利用等角的三角比解决问题(利用一线三等角模型或者拆分特殊角来发现等角),其次选择利用相似三角形中的比例线段解决问题。
二次函数中的角相等问题比较灵活,同学们在遇到具体问题时具体分析,合理构造等角,解决问题。
答案解析
例1.【答案】(1);(2)18;(3).
【分析】(1)先求出C、B的坐标,代入抛物线的解析式即可得到结论;
(2)求出D的坐标,由计算即可;
(3)过点作,垂足为点,由△ABC的面积求出CH的长,在Rt△BCH中,求出tan∠CBH,在Rt△BOE中,根据tan∠BEO,即可得出E的坐标.
【详解】(1)∵抛物线与轴交于点,,∴.∵,∴.又点在轴的负半轴上,∴.
∵抛物线经过点和点,
∴,解得,
∴这条抛物线的表达式为;
(2)由,得顶点的坐标是.联结,
∵点的坐标是,点的坐标是,又,,∴;
(3)过点作,垂足为点.∵,,
∴.在Rt中,,,,∴;
在Rt中,,.
∵,∴,得,
∴点的坐标为.
考点:二次函数的图象,二元一次方程组,三角函数,三角形的面积.
变式训练1
1.【答案】见解析.
【解析】解:(1)∵抛物线对称轴为x=-1
即
∴b=-1
将(0,4)代入中,得c=4,
∴
(2)过P作轴于点E
易证得△PEB∽△BOC,
∴
设,则
①当点P在x轴上方时:
解得(舍)
②当点P在x轴下方时:
解得(舍)
综上所述,或.
2.【答案】见解析.
【解析】解:(1)y=ax2+bx﹣3=a(x+3)(x﹣1),
解得:a=1,
故抛物线的表达式为:y=x2+2x﹣3;
(2)由抛物线的表达式知,点C、D的坐标分别为(0,﹣3)、(﹣1,﹣4),
由点C、D的坐标知,直线CD的表达式为:y=x﹣3;
tan∠BCO,则cos∠BCO;
①当点P(P′)在点C的右侧时,
∵∠PAB=∠BCO,
故P′B∥y轴,则点P′(1,﹣2);
当点P在点C的左侧时,
设直线PB交y轴于点H,过点H作HN⊥BC于点N,
∵∠PAB=∠BCO,
∴△BCH为等腰三角形, BC=2CH cos∠BCO=2×CH,
解得:CH,则OH=3﹣CH,故点H(0,),
由点B、H的坐标得,直线BH的表达式为:yx,
联立yx,y=x2+2x﹣3,解得:,
所以点P的坐标为(1,﹣2)或(﹣5,﹣8);
②∵∠PAB=∠BCO,而tan∠BCO,
故设直线AP的表达式为:yx+s,将点A的坐标代入上式并解得:s=1,
故直线AP的表达式为:yx+1,
联立①③并解得:,故点N(,);
设△AMN的外接圆为圆R,
当∠ANM=45°时,则∠ARM=90°,设圆心R的坐标为(m,n),
∵∠GRA+∠MRH=90°,∠MRH+∠RMH=90°,
∴∠RMH=∠GAR,
∵AR=MR,∠AGR=∠RHM=90°,
∴△AGR≌△RHM(AAS),
∴AG=m+3=RH,RG=﹣n=MH,
∴点M(m+n,n﹣m﹣3),
将点M的坐标代入抛物线表达式得:n﹣m﹣3=(m+n)2+2(m+n)﹣3,
由题意得:AR=NR,即(m+3)2=(m)2+()2,解得:,
故点M(,).
例2.【答案】见解析.
【解析】解:(1)根据题意得,
解得.
故抛物线的解析式为;
(2)二次函数的对称轴是x=1,
当x=0时,y=3,
则C(0,3),
点C关于对称轴的对应点,
设直线BC的解析式为y=kx+3,
则k=-1.
则直线BC的解析式为,
设与BC平行的直线AP的解析式为,
则,
解得.
则与平行的直线的解析式为,
联立,
解得,(舍去).
即P(4,-5).
综上所述,P(2,3)、(4,-5).
变式训练2
1.【答案】见解析.
【解析】解:(1)直线yx+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
所以抛物线的表达式为:yx2x+2;
(2)作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
由点A、B′的坐标得,直线AB′的表达式为:yx﹣2,
联立yx2x+2,yx﹣2,解得:x=3或﹣2,
故点P的坐标为(3,)或(﹣2,﹣3);
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:mn2n;
②mn2n,
∵0,故m有最大值,当n时,m的最大值为,
而m>0,
故0<m时,符合条件的N点的个数有2个.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
