【2023中考二轮复习】特殊角的存在性问题专题探究(含答案)
文档属性
| 名称 | 【2023中考二轮复习】特殊角的存在性问题专题探究(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 10:40:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023年中考数学存在性问题—— 特殊角的存在性问题专题探究
特殊角的存在性问题也是近年来各地中考的热点,其图形复杂,不确定因素较多,解题有一定的难度.因此对此类问题建立解题模型,则可以大大降低学生思维难度。
解题攻略
【基本概念】
特殊角存在性问题在坐标系中可以由以下几种方式得到:
等腰直角三角形的性质;
平行线的性质;
等边三角形的性质;
等角三角函数相等。
直角三角形性质。
2.【基本题型】
(1)30°,60°特殊角
(2)90°的特殊角
(3)45°的特殊角
(4)15°的特殊角
3.【解题思路】
(1)运用三角函数值;
(2)遇45°构造等腰直角三角形;
(3)遇30°,60°构造等边三角形;
(4)遇90°构造直角三角形。
典例剖析
1.遇45°构造等腰直角三角形
例1.如图,抛物线与y=-x2+x+2与直线y=x+2交于C,D两点,点P是直线CD上方的抛物线上一点,PE⊥x轴于点E,交CD于点F,∠PCF=45°,求点P的坐标.
例2.如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是四边形OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
变式训练1
1.如图,已知直线与抛物线相交于,两点,抛物线的顶点是,点在轴上.
(1)求抛物线的解析式;
(2)若点是轴上一点,点是坐标平面内一点,当以、、、为顶点的四边形是矩形时,求点的坐标.
(3)在抛物线上是否存在点,使,若存在,请直接写出点的横坐标;若不存在,说明理由.
2.遇30°,60°构造等边三角形
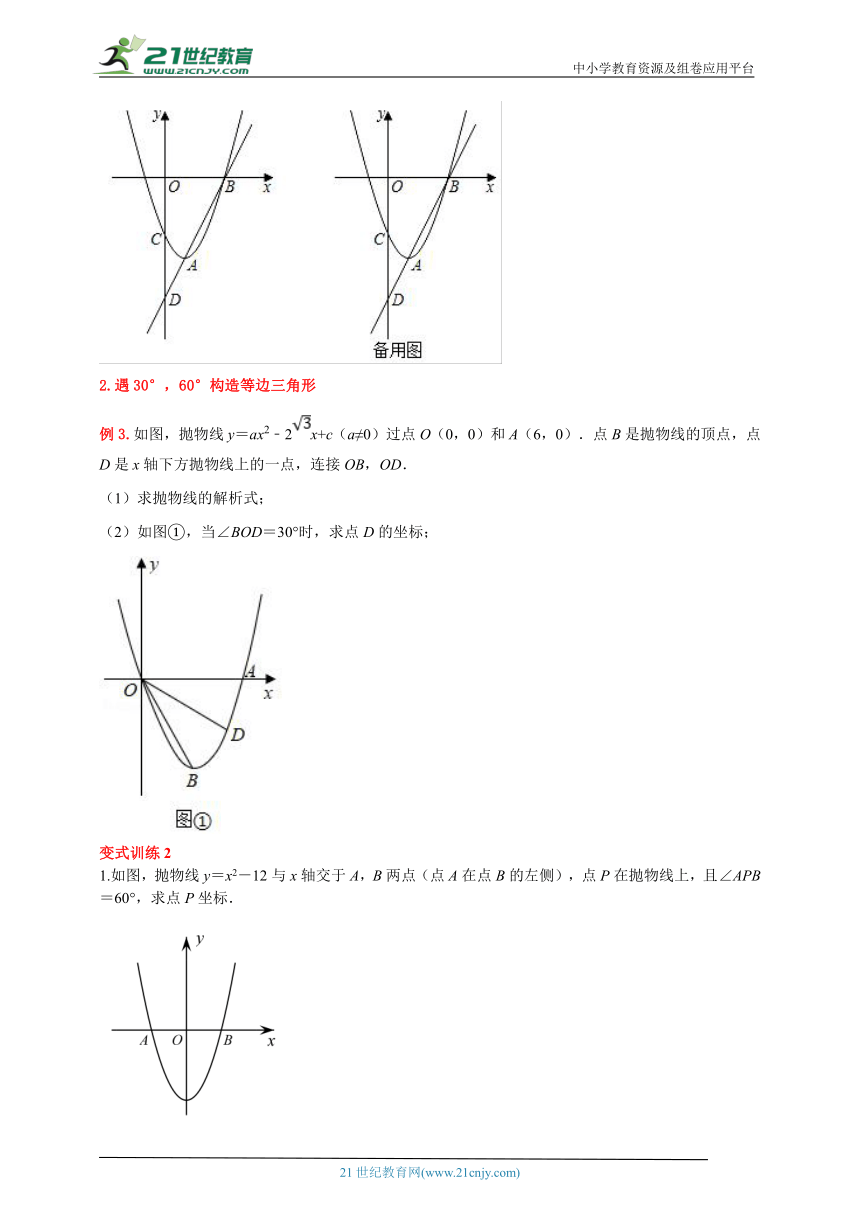
例3.如图,抛物线y=ax2﹣2x+c(a≠0)过点O(0,0)和A(6,0).点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接OB,OD.
(1)求抛物线的解析式;
(2)如图①,当∠BOD=30°时,求点D的坐标;
变式训练2
1.如图,抛物线y=x2-12与x轴交于A,B两点(点A在点B的左侧),点P在抛物线上,且∠APB=60°,求点P坐标.
3.遇90°构造直角三角形。
例3.已知二次函数图象过点A(﹣2,0),B(4,0),C(0,4).
(1)求二次函数的解析式.
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标;若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角θ,且tanθ,求点K的坐标.
变式训练3
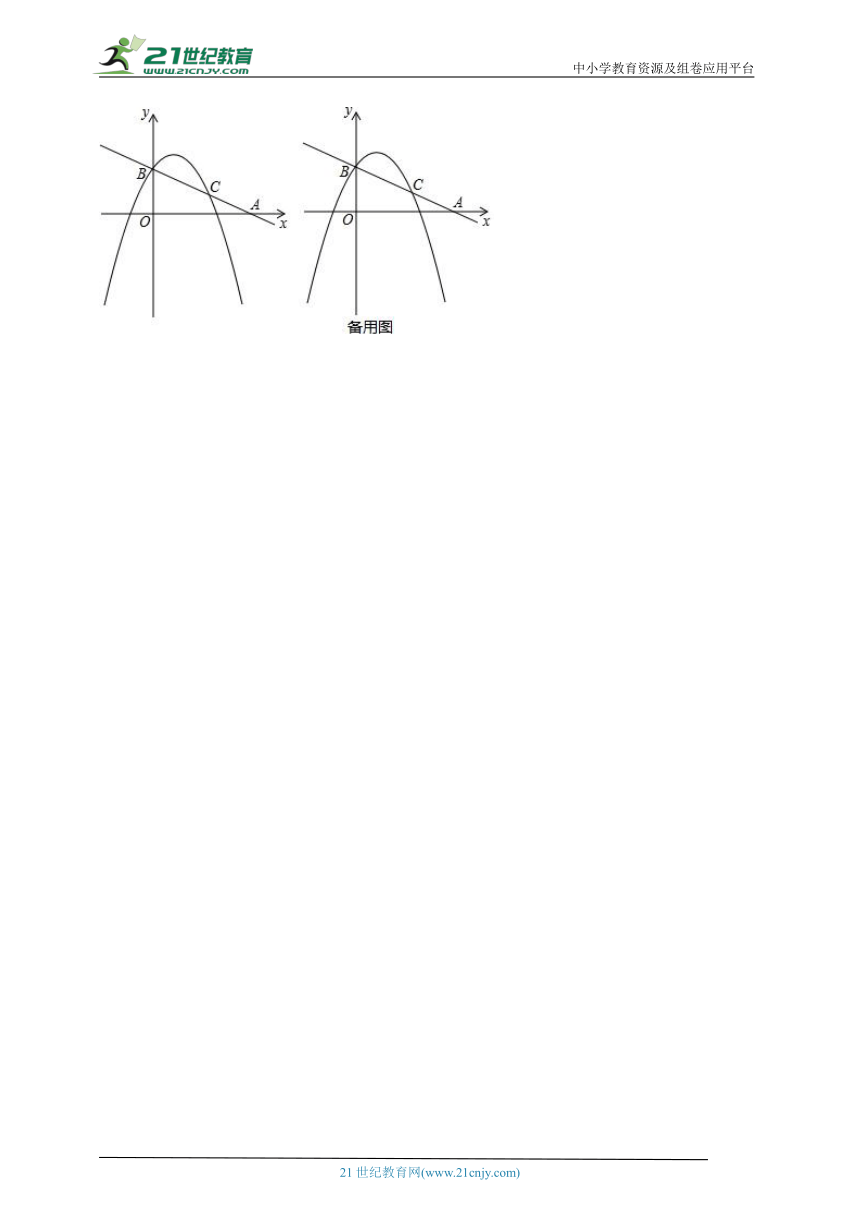
如图,在平面直角坐标系中,直线yx+2与x轴交于点A,与y轴交于点B,抛物线yx2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
答案解析
例1.【解答】延长PC交x轴于点A,过点A作AG⊥AC,交直线CD于点G,设A(a,0),
易得G(a-2,-a),代入y=x+2,得a=- ,∴A(-,0),∴AC:y=3x+2.
联立,得P(,)
例2.【答案】见解析.
【解析】解:(1)OA=2=BC,函数的对称轴为x=1,则x1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b②,
联立①②并解得,
故抛物线的表达式为:yx2x③;
(2)由抛物线的表达式得,点M(1,3)、点D(4,0);
∵△ADR的面积是四边形OABC的面积的,
∴AD×|yR|OA×OB,则6×|yR|2,解得:yR=±④,
联立③④,解得,
故点R的坐标为(1,4)或(1,4)或(1,﹣4)或(1,﹣4);
(3)作△PEQ的外接圆R,
∵∠PQE=45°,
故∠PRE=90°,则△PRE为等腰直角三角形,
当直线MD上存在唯一的点Q,则RQ⊥MD,
点M、D的坐标分别为(1,4)、(4,0),
则ME=4,ED=4﹣1=3,则MD=5,
过点R作RH⊥ME于点H,
设点P(1,2m),则PH=HE=HR=m,
则圆R的半径为m,则点R(1+m,m),
S△MED=S△MRD+S△MRE+S△DRE,
即EM EDMD×RQED yRME RH,
∴4×35m4×m3×m,解得m=6084,
故点P(1,120168).
变式训练1
【解答】解:(1)将点代入直线得,
,
,
直线,
当时,代入直线得:,
解得:,
点坐标,
设抛物线表达式为,将点代入抛物线得,
,
解得:,
抛物线表达式;
(2)当以、、、为顶点的四边形是矩形时,有两种情况:
①如图,当为边时,
设点,
已知点,点
,,,
,即,
解得,
即点的坐标,
延长交轴于点,作轴于,交的延长线于点.
由,可得,
,
,
,
②如图,当为对角线时,
取线段的中点,作辅助圆,与轴交于点,,作轴于点,
点坐标,,即,
由①可得线段,
半径,
在△中,,,
,
根据垂径定理可得,,
点坐标,点坐标;
综上所述,当以、、、为顶点的四边形是矩形时,点坐标为:或或或;
(3)存在点的横坐标为或,使.
理由如下:假设存在满足条件的点,如图,
当四边形为正方形,且点,分别在直线和直线上时,,
设过线段中点,且与线段垂直的直线:,
将点代入得:,
解得,
直线为,
设点点坐标,
在中,,,
,
解得,
,
解得,,
点坐标,点坐标,
设直线表达式为:,将点,点代入得,
,
解得,
直线的表达式为,
同理可得直线的表达式为,
联立直线与抛物线可得,
,
解得,,
同理联立直线与抛物线可解得,,
点的横坐标为或.
例3.【答案】见解析.
【解析】解:(1)把点O(0,0)和A(6,0)代入y=ax2﹣2x+c中,
得到,
解得,
∴抛物线的解析式为yx2﹣2x.
(2)设抛物线的对称轴交x轴于M,与OD交于点N.
∵yx2﹣2x(x﹣3)2﹣3,
∴顶点B(3,﹣3),M(3,0),
∴OM=3.BM=3,
∴tan∠MOB,
∴∠MOB=60°,
∵∠BOD=30°,
∴∠MON=∠MOB﹣∠BOD=30°,
∴MN=OM tam30°,
∴N(3,),
∴直线ON的解析式为yx,
由,解得或,
∴D(5,).
变式训练2
解:A(-,0),B(,0),在y轴上取点M(0,2),设P(t,t2-12),易得∠AMB=120°,
(1)点P在x轴上方时,以M为圆心,MA=4为半径画圆,与抛物线交于点P,
点P即为所求,MP2=MB2=16,t2+(t2-12-2)2=16,t4-27t2+180=0,
(t2-12)(t2-15)=0,t2=12或t2=15,∴P(±,0)(舍去),(±,3);
(2)当点P在x轴下方时,M(0,-2),MP2=MB2,t2+(t2-12+2)2=16,
t2=12(舍)或t2=7,t=±,P(±,-5);
故点P的坐标为(±,3),P(±,-5).
例3.【答案】见解析.
【解析】解:(1)∵二次函数图象过点B(4,0),点A(﹣2,0),
∴设二次函数的解析式为y=a(x+2)(x﹣4),
∵二次函数图象过点C(0,4),
∴4=a(0+2)(0﹣4),
∴a,
∴二次函数的解析式为y(x+2)(x﹣4)x2+x+4;
(2)存在,
理由如下:取BC中点Q,连接MQ,
∵点A(﹣2,0),B(4,0),C(0,4),点P是AC中点,点Q是BC中点,
∴P(﹣1,2),点Q(2,2),BC4,
设直线BP解析式为:y=kx+b,
由题意可得:,
解得:
∴直线BP的解析式为:yx,
∵∠BMC=90°
∴点M在以BC为直径的圆上,
∴设点M(c,c),
∵点Q是Rt△BCM的中点,
∴MQBC=2,
∴MQ2=8,
∴(c﹣2)2+(c2)2=8,
∴c=4或,
当c=4时,点B,点M重合,即c=4,不合题意舍去,
∴c,则点M坐标(,),
故线段PB上存在点M(,),使得∠BMC=90°;
(3)过点D作DE⊥BC于点E,设直线DK与BC交于点N,
∵点A(﹣2,0),B(4,0),C(0,4),点D是AB中点,
∴点D(1,0),OB=OC=4,AB=6,BD=3,
∴∠OBC=45°,
∵DE⊥BC,
∴∠EDB=∠EBD=45°,
∴DE=BE,
∵点B(4,0),C(0,4),
∴直线BC解析式为:y=﹣x+4,
设点E(n,﹣n+4),
∴﹣n+4,
∴n,
∴点E(,),
在Rt△DNE中,NE.
①若DK与射线EC交于点N(m,4﹣m),
∵NE=BN﹣BE,
∴(4﹣m),
∴m,
∴点N(,),
∴直线DK解析式为:y=4x﹣4,
联立y=4x﹣4,x2+x+4
得:点K坐标为(2,4)或(﹣8,﹣36);
②若DK与射线EB交于N(m,4﹣m),
∵NE=BE﹣BN,
∴(4﹣m),
∴m,
∴点N(,),
∴直线DK解析式为:yx,
联立yx,x2+x+4,
得点K坐标为(,)或(,),
综上所述:点K的坐标为(2,4)或(﹣8,﹣36)或(,)或(,).
变式训练3
【答案】见解析.
【解析】解:(1)直线yx+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
所以抛物线的表达式为:yx2x+2;
(2)作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
由点A、B′的坐标得,直线AB′的表达式为:yx﹣2,
联立yx2x+2,yx﹣2,解得:x=3或﹣2,
故点P的坐标为(3,)或(﹣2,﹣3);
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:mn2n;
②mn2n,
∵0,故m有最大值,当n时,m的最大值为,
而m>0,
故0<m时,符合条件的N点的个数有2个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2023年中考数学存在性问题—— 特殊角的存在性问题专题探究
特殊角的存在性问题也是近年来各地中考的热点,其图形复杂,不确定因素较多,解题有一定的难度.因此对此类问题建立解题模型,则可以大大降低学生思维难度。
解题攻略
【基本概念】
特殊角存在性问题在坐标系中可以由以下几种方式得到:
等腰直角三角形的性质;
平行线的性质;
等边三角形的性质;
等角三角函数相等。
直角三角形性质。
2.【基本题型】
(1)30°,60°特殊角
(2)90°的特殊角
(3)45°的特殊角
(4)15°的特殊角
3.【解题思路】
(1)运用三角函数值;
(2)遇45°构造等腰直角三角形;
(3)遇30°,60°构造等边三角形;
(4)遇90°构造直角三角形。
典例剖析
1.遇45°构造等腰直角三角形
例1.如图,抛物线与y=-x2+x+2与直线y=x+2交于C,D两点,点P是直线CD上方的抛物线上一点,PE⊥x轴于点E,交CD于点F,∠PCF=45°,求点P的坐标.
例2.如图,在直角坐标系中,四边形OABC是平行四边形,经过A(﹣2,0),B,C三点的抛物线y=ax2+bx(a<0)与x轴的另一个交点为D,其顶点为M,对称轴与x轴交于点E.
(1)求这条抛物线对应的函数表达式;
(2)已知R是抛物线上的点,使得△ADR的面积是四边形OABC的面积的,求点R的坐标;
(3)已知P是抛物线对称轴上的点,满足在直线MD上存在唯一的点Q,使得∠PQE=45°,求点P的坐标.
变式训练1
1.如图,已知直线与抛物线相交于,两点,抛物线的顶点是,点在轴上.
(1)求抛物线的解析式;
(2)若点是轴上一点,点是坐标平面内一点,当以、、、为顶点的四边形是矩形时,求点的坐标.
(3)在抛物线上是否存在点,使,若存在,请直接写出点的横坐标;若不存在,说明理由.
2.遇30°,60°构造等边三角形
例3.如图,抛物线y=ax2﹣2x+c(a≠0)过点O(0,0)和A(6,0).点B是抛物线的顶点,点D是x轴下方抛物线上的一点,连接OB,OD.
(1)求抛物线的解析式;
(2)如图①,当∠BOD=30°时,求点D的坐标;
变式训练2
1.如图,抛物线y=x2-12与x轴交于A,B两点(点A在点B的左侧),点P在抛物线上,且∠APB=60°,求点P坐标.
3.遇90°构造直角三角形。
例3.已知二次函数图象过点A(﹣2,0),B(4,0),C(0,4).
(1)求二次函数的解析式.
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标;若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角θ,且tanθ,求点K的坐标.
变式训练3
如图,在平面直角坐标系中,直线yx+2与x轴交于点A,与y轴交于点B,抛物线yx2+bx+c过点B且与直线相交于另一点C(,).
(1)求抛物线的解析式;
(2)点P是抛物线上的一动点,当∠PAO=∠BAO时,求点P的坐标;
(3)点N(n,0)(0<n)在x轴的正半轴上,点M(0,m)是y轴正半轴上的一动点,且满足∠MNC=90°.
①求m与n之间的函数关系式;
②当m在什么范围时,符合条件的N点的个数有2个?
答案解析
例1.【解答】延长PC交x轴于点A,过点A作AG⊥AC,交直线CD于点G,设A(a,0),
易得G(a-2,-a),代入y=x+2,得a=- ,∴A(-,0),∴AC:y=3x+2.
联立,得P(,)
例2.【答案】见解析.
【解析】解:(1)OA=2=BC,函数的对称轴为x=1,则x1①,
将点A的坐标代入抛物线表达式得:0=4a﹣2b②,
联立①②并解得,
故抛物线的表达式为:yx2x③;
(2)由抛物线的表达式得,点M(1,3)、点D(4,0);
∵△ADR的面积是四边形OABC的面积的,
∴AD×|yR|OA×OB,则6×|yR|2,解得:yR=±④,
联立③④,解得,
故点R的坐标为(1,4)或(1,4)或(1,﹣4)或(1,﹣4);
(3)作△PEQ的外接圆R,
∵∠PQE=45°,
故∠PRE=90°,则△PRE为等腰直角三角形,
当直线MD上存在唯一的点Q,则RQ⊥MD,
点M、D的坐标分别为(1,4)、(4,0),
则ME=4,ED=4﹣1=3,则MD=5,
过点R作RH⊥ME于点H,
设点P(1,2m),则PH=HE=HR=m,
则圆R的半径为m,则点R(1+m,m),
S△MED=S△MRD+S△MRE+S△DRE,
即EM EDMD×RQED yRME RH,
∴4×35m4×m3×m,解得m=6084,
故点P(1,120168).
变式训练1
【解答】解:(1)将点代入直线得,
,
,
直线,
当时,代入直线得:,
解得:,
点坐标,
设抛物线表达式为,将点代入抛物线得,
,
解得:,
抛物线表达式;
(2)当以、、、为顶点的四边形是矩形时,有两种情况:
①如图,当为边时,
设点,
已知点,点
,,,
,即,
解得,
即点的坐标,
延长交轴于点,作轴于,交的延长线于点.
由,可得,
,
,
,
②如图,当为对角线时,
取线段的中点,作辅助圆,与轴交于点,,作轴于点,
点坐标,,即,
由①可得线段,
半径,
在△中,,,
,
根据垂径定理可得,,
点坐标,点坐标;
综上所述,当以、、、为顶点的四边形是矩形时,点坐标为:或或或;
(3)存在点的横坐标为或,使.
理由如下:假设存在满足条件的点,如图,
当四边形为正方形,且点,分别在直线和直线上时,,
设过线段中点,且与线段垂直的直线:,
将点代入得:,
解得,
直线为,
设点点坐标,
在中,,,
,
解得,
,
解得,,
点坐标,点坐标,
设直线表达式为:,将点,点代入得,
,
解得,
直线的表达式为,
同理可得直线的表达式为,
联立直线与抛物线可得,
,
解得,,
同理联立直线与抛物线可解得,,
点的横坐标为或.
例3.【答案】见解析.
【解析】解:(1)把点O(0,0)和A(6,0)代入y=ax2﹣2x+c中,
得到,
解得,
∴抛物线的解析式为yx2﹣2x.
(2)设抛物线的对称轴交x轴于M,与OD交于点N.
∵yx2﹣2x(x﹣3)2﹣3,
∴顶点B(3,﹣3),M(3,0),
∴OM=3.BM=3,
∴tan∠MOB,
∴∠MOB=60°,
∵∠BOD=30°,
∴∠MON=∠MOB﹣∠BOD=30°,
∴MN=OM tam30°,
∴N(3,),
∴直线ON的解析式为yx,
由,解得或,
∴D(5,).
变式训练2
解:A(-,0),B(,0),在y轴上取点M(0,2),设P(t,t2-12),易得∠AMB=120°,
(1)点P在x轴上方时,以M为圆心,MA=4为半径画圆,与抛物线交于点P,
点P即为所求,MP2=MB2=16,t2+(t2-12-2)2=16,t4-27t2+180=0,
(t2-12)(t2-15)=0,t2=12或t2=15,∴P(±,0)(舍去),(±,3);
(2)当点P在x轴下方时,M(0,-2),MP2=MB2,t2+(t2-12+2)2=16,
t2=12(舍)或t2=7,t=±,P(±,-5);
故点P的坐标为(±,3),P(±,-5).
例3.【答案】见解析.
【解析】解:(1)∵二次函数图象过点B(4,0),点A(﹣2,0),
∴设二次函数的解析式为y=a(x+2)(x﹣4),
∵二次函数图象过点C(0,4),
∴4=a(0+2)(0﹣4),
∴a,
∴二次函数的解析式为y(x+2)(x﹣4)x2+x+4;
(2)存在,
理由如下:取BC中点Q,连接MQ,
∵点A(﹣2,0),B(4,0),C(0,4),点P是AC中点,点Q是BC中点,
∴P(﹣1,2),点Q(2,2),BC4,
设直线BP解析式为:y=kx+b,
由题意可得:,
解得:
∴直线BP的解析式为:yx,
∵∠BMC=90°
∴点M在以BC为直径的圆上,
∴设点M(c,c),
∵点Q是Rt△BCM的中点,
∴MQBC=2,
∴MQ2=8,
∴(c﹣2)2+(c2)2=8,
∴c=4或,
当c=4时,点B,点M重合,即c=4,不合题意舍去,
∴c,则点M坐标(,),
故线段PB上存在点M(,),使得∠BMC=90°;
(3)过点D作DE⊥BC于点E,设直线DK与BC交于点N,
∵点A(﹣2,0),B(4,0),C(0,4),点D是AB中点,
∴点D(1,0),OB=OC=4,AB=6,BD=3,
∴∠OBC=45°,
∵DE⊥BC,
∴∠EDB=∠EBD=45°,
∴DE=BE,
∵点B(4,0),C(0,4),
∴直线BC解析式为:y=﹣x+4,
设点E(n,﹣n+4),
∴﹣n+4,
∴n,
∴点E(,),
在Rt△DNE中,NE.
①若DK与射线EC交于点N(m,4﹣m),
∵NE=BN﹣BE,
∴(4﹣m),
∴m,
∴点N(,),
∴直线DK解析式为:y=4x﹣4,
联立y=4x﹣4,x2+x+4
得:点K坐标为(2,4)或(﹣8,﹣36);
②若DK与射线EB交于N(m,4﹣m),
∵NE=BE﹣BN,
∴(4﹣m),
∴m,
∴点N(,),
∴直线DK解析式为:yx,
联立yx,x2+x+4,
得点K坐标为(,)或(,),
综上所述:点K的坐标为(2,4)或(﹣8,﹣36)或(,)或(,).
变式训练3
【答案】见解析.
【解析】解:(1)直线yx+2与x轴交于点A,与y轴交于点B,则点A、B的坐标分别为(4,0)、(0,2),
将点B、C的坐标代入抛物线表达式得,解得,
所以抛物线的表达式为:yx2x+2;
(2)作点B关于x轴的对称点B′(0,﹣2),连接AB′交抛物线于点P(P′),则∠PAO=∠BAO,
由点A、B′的坐标得,直线AB′的表达式为:yx﹣2,
联立yx2x+2,yx﹣2,解得:x=3或﹣2,
故点P的坐标为(3,)或(﹣2,﹣3);
(3)①过点C作CH⊥x轴于点H,
∵∠MNC=90°,
∴∠MNO+∠CNH=90°,
∠CNH+∠NCH=90°,
∴∠MNO=∠NCH,
∴tan∠MNO=tan∠NCH,即,即,
解得:mn2n;
②mn2n,
∵0,故m有最大值,当n时,m的最大值为,
而m>0,
故0<m时,符合条件的N点的个数有2个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
