直线和圆的位置关系[上学期]
图片预览




文档简介
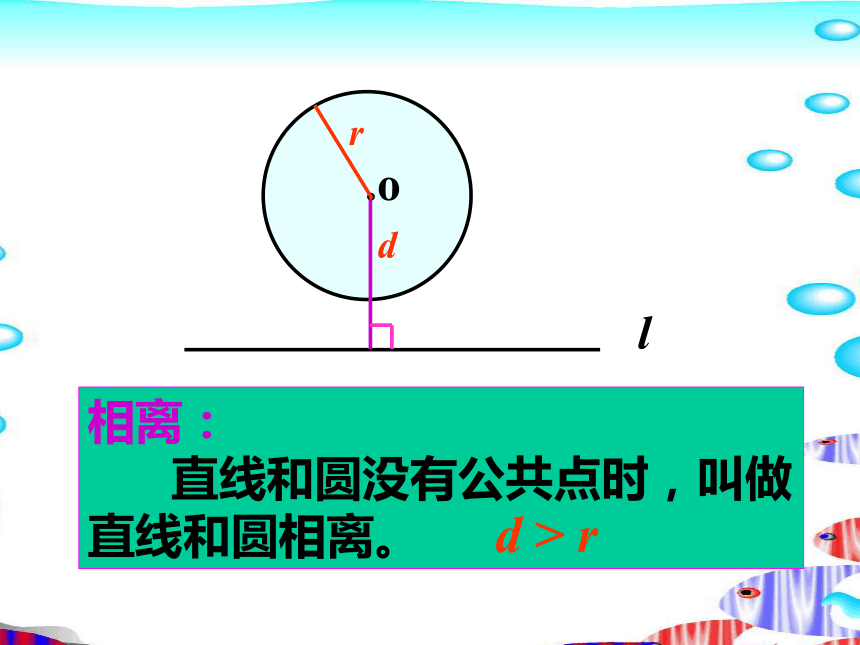
课件21张PPT。直线和圆的位置关系直线和圆的位置关系.olrd相离:
直线和圆没有公共点时,叫做
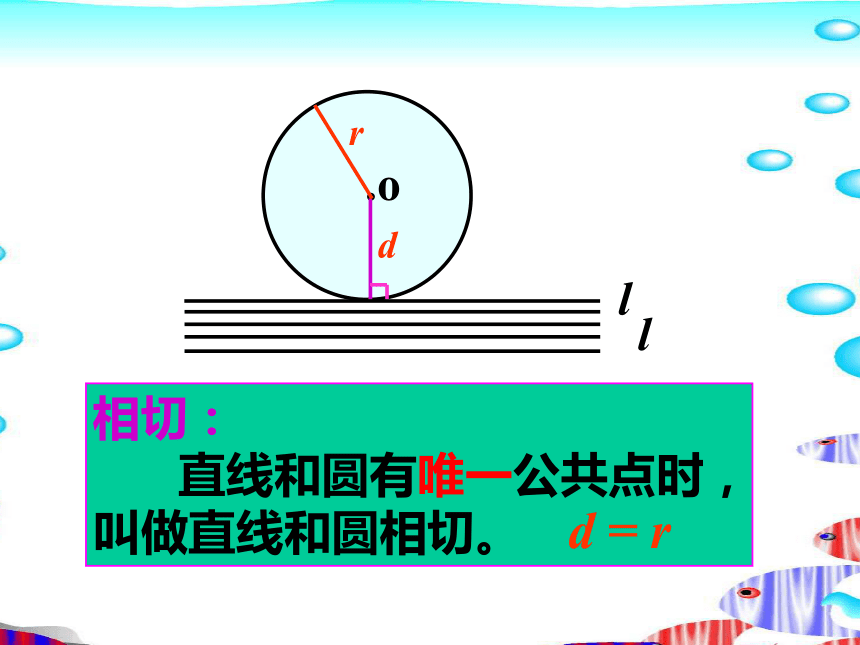
直线和圆相离。d > r.ord相切:
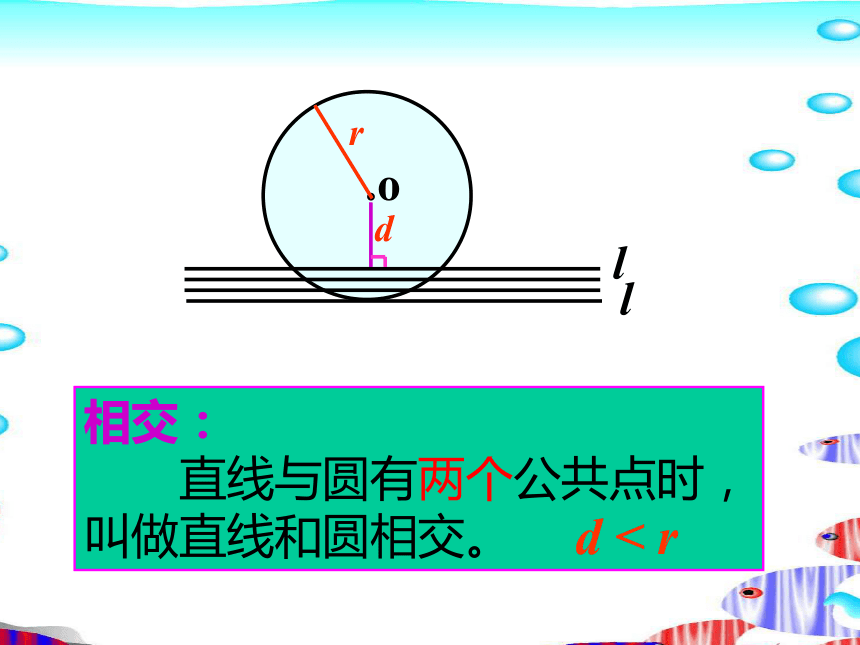
直线和圆有唯一公共点时,叫做直线和圆相切。ld = r.ordl相交:
直线与圆有两个公共点时,
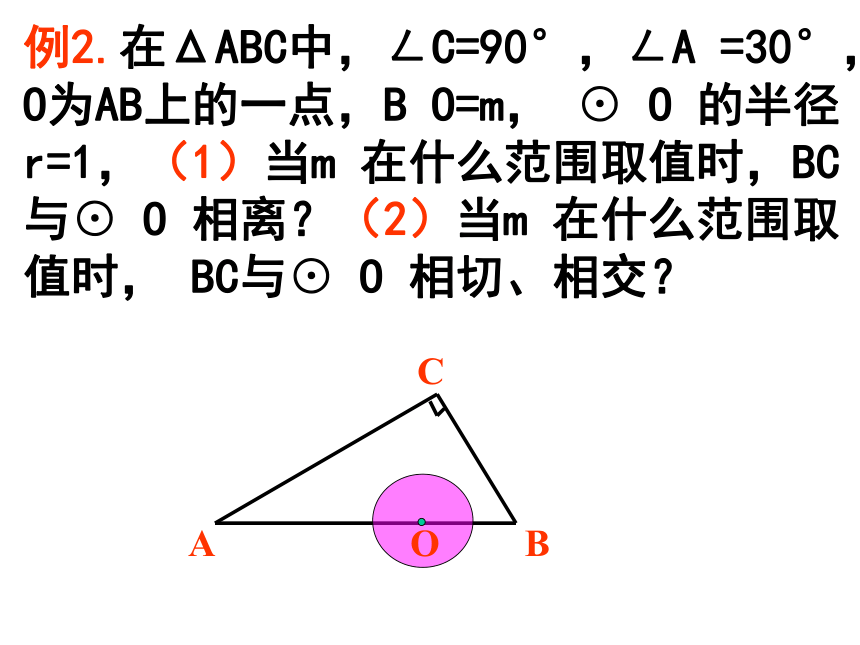
叫做直线和圆相交。 d < r练一练:1.已知圆的半径等于5cm,圆心到直线l的距离为(1)4cm ;(2)5cm ;(3)6cm ,直线l和圆分别有几个公共点?分别说出直线与圆的位置关系。 2.已知圆的半径等于10cm,直线与圆只有一个公共点,求圆心到直线的距离。3.如果☉O的直径为10cm ,圆心O到直线AB的距离为10cm,那么☉O与直线AB有怎样的位置关系?例2.在ΔABC中,ㄥC=90°,ㄥA =30°,O为AB上的一点,B O=m, ☉ O 的半径r=1,(1)当m 在什么范围取值时,BC与☉ O 相离?(2)当m 在什么范围取值时, BC与☉ O 相切、相交? 台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力。 据气象观测,距我县(点A表示)正西方向 80 km 的B处桑美台风,该台风中心现正以 20 km/h 的速度沿北偏东60°方向向C移动,其影响范围为50 km .
(1)我县是否会受到这
次台风的影响?为什么?
(2)若会受到台风影响,
那么台风影响我县的持续
时间多长?
80km20 km/h我们也是小专家! 谢谢,再见! 从圆外一点,可引圆的两条切线,它
们的切线长相等;这一点和圆心的连线,
平分这两条切线之间的夹角。 经过半径的外端且垂直于这条半径的直线是圆的切线。 圆的切线,垂直于过切点的半径。直线AT为⊙O切线OA ?AT知识运用)1)23(试一试 以Rt△ABC的直角边AB为直径作⊙O交斜边BC于点P,Q是AC的中点,PQ为⊙O的切线吗?为什么?)12()34( Q是AC的中点能得出什么结论呢? △ABC的内切圆⊙O与AC、AB、BC 分别相切与点D、E、F,且AB=10,BC=18,AC=12,试求AE,BF,CD的长. 若设AE=AD =x,
则:BE=BF=10-x ;
CF=CD=18-(10-x)=x+8 可得方程:x+(x+8)=12 梯形ABCD中,AD∥BC,∠BCD=90°,
以CD为直径的半圆切AB于点E,这个梯形
的面积为21cm2,周长为20cm,则半⊙O的
半径为多少?分析:由题意可知: AD=AE;BE=BC . 若设AD=x ,BE=y,半径为r;由已知可得关系式:议一议通过这节课复习,你掌握了哪些知识? 1、进一步掌握了直线与圆的三种位置关系; 2、掌握了切线长定理,并利用它解决一些问题; 3、会利用切线的识别和特征解决一些问题; 4、会用所学的直线与圆的知识解决一些现实问题; 5、进一步学习了数形结合、方程思想的数学方法。 作业:1、如图AB=15,BC=14,AC=13,
⊙O为△ABC的内切圆,切点分别
是D、E、F,则AD+BE+CF= ( )E2、PA、PB分别切⊙O于A、B,OP交弧AB于点C,连接AB、AC,试说明AC平分∠PAB.
直线和圆没有公共点时,叫做
直线和圆相离。d > r.ord相切:
直线和圆有唯一公共点时,叫做直线和圆相切。ld = r.ordl相交:
直线与圆有两个公共点时,
叫做直线和圆相交。 d < r练一练:1.已知圆的半径等于5cm,圆心到直线l的距离为(1)4cm ;(2)5cm ;(3)6cm ,直线l和圆分别有几个公共点?分别说出直线与圆的位置关系。 2.已知圆的半径等于10cm,直线与圆只有一个公共点,求圆心到直线的距离。3.如果☉O的直径为10cm ,圆心O到直线AB的距离为10cm,那么☉O与直线AB有怎样的位置关系?例2.在ΔABC中,ㄥC=90°,ㄥA =30°,O为AB上的一点,B O=m, ☉ O 的半径r=1,(1)当m 在什么范围取值时,BC与☉ O 相离?(2)当m 在什么范围取值时, BC与☉ O 相切、相交? 台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力。 据气象观测,距我县(点A表示)正西方向 80 km 的B处桑美台风,该台风中心现正以 20 km/h 的速度沿北偏东60°方向向C移动,其影响范围为50 km .
(1)我县是否会受到这
次台风的影响?为什么?
(2)若会受到台风影响,
那么台风影响我县的持续
时间多长?
80km20 km/h我们也是小专家! 谢谢,再见! 从圆外一点,可引圆的两条切线,它
们的切线长相等;这一点和圆心的连线,
平分这两条切线之间的夹角。 经过半径的外端且垂直于这条半径的直线是圆的切线。 圆的切线,垂直于过切点的半径。直线AT为⊙O切线OA ?AT知识运用)1)23(试一试 以Rt△ABC的直角边AB为直径作⊙O交斜边BC于点P,Q是AC的中点,PQ为⊙O的切线吗?为什么?)12()34( Q是AC的中点能得出什么结论呢? △ABC的内切圆⊙O与AC、AB、BC 分别相切与点D、E、F,且AB=10,BC=18,AC=12,试求AE,BF,CD的长. 若设AE=AD =x,
则:BE=BF=10-x ;
CF=CD=18-(10-x)=x+8 可得方程:x+(x+8)=12 梯形ABCD中,AD∥BC,∠BCD=90°,
以CD为直径的半圆切AB于点E,这个梯形
的面积为21cm2,周长为20cm,则半⊙O的
半径为多少?分析:由题意可知: AD=AE;BE=BC . 若设AD=x ,BE=y,半径为r;由已知可得关系式:议一议通过这节课复习,你掌握了哪些知识? 1、进一步掌握了直线与圆的三种位置关系; 2、掌握了切线长定理,并利用它解决一些问题; 3、会利用切线的识别和特征解决一些问题; 4、会用所学的直线与圆的知识解决一些现实问题; 5、进一步学习了数形结合、方程思想的数学方法。 作业:1、如图AB=15,BC=14,AC=13,
⊙O为△ABC的内切圆,切点分别
是D、E、F,则AD+BE+CF= ( )E2、PA、PB分别切⊙O于A、B,OP交弧AB于点C,连接AB、AC,试说明AC平分∠PAB.
