直线和圆的位置关系[上学期]

课件19张PPT。直线和圆的位置关系 安岳外国语学校：龙强2、连结直线外一点与直线所
有点的线段中,最短的是______？ 1.直线外一点到这条直线
垂线段的长度叫点到直线 的距离。垂线段
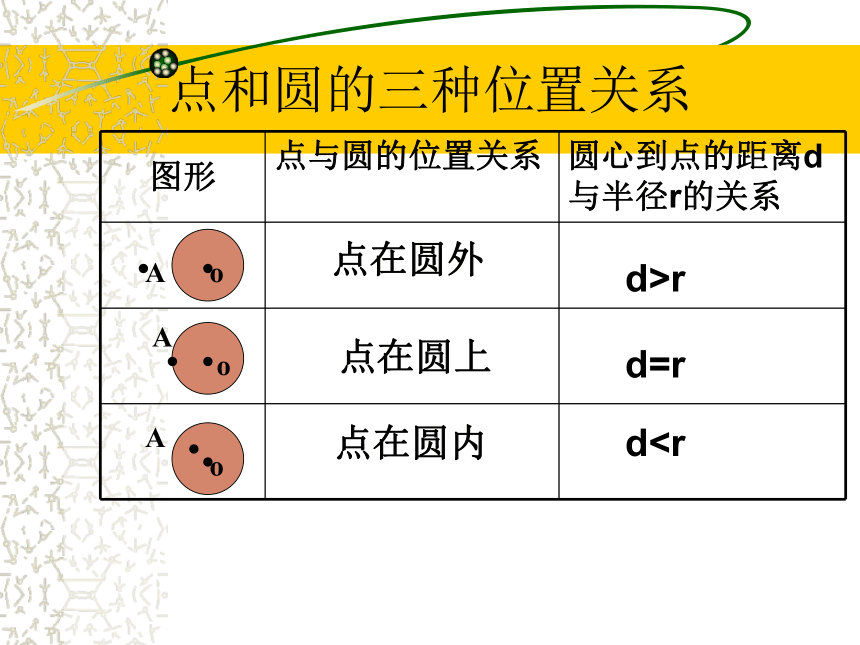
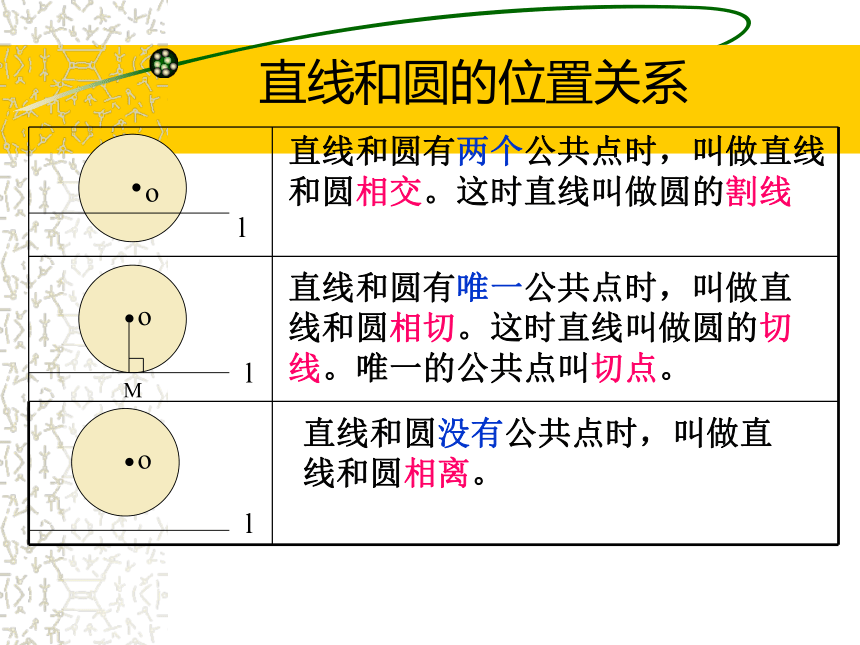
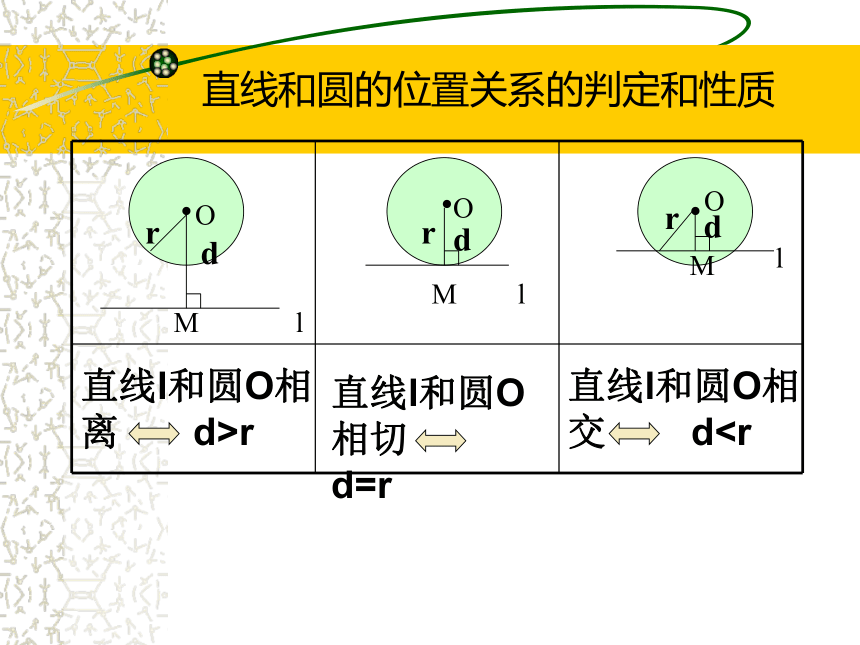
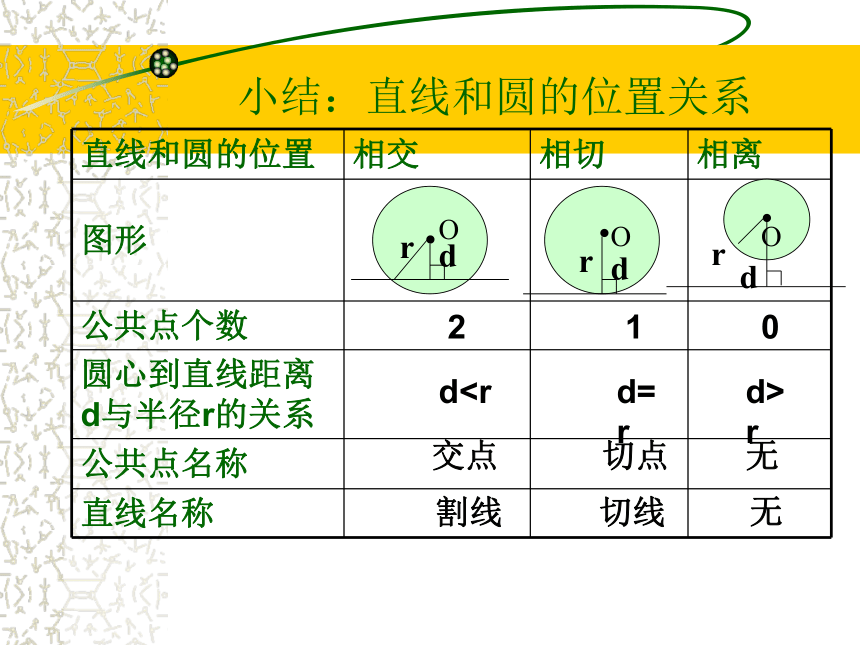
a .AD什么叫点到直线的距离？点和圆的三种位置关系AAA??????ooo点在圆外点在圆上点在圆内d>rd=rdrdddrrr小结：直线和圆的位置关系210dr交点切点无 割线 切线 无O?drOl?drO ?dr总结：判定直线 与圆的位置关系的方法有____种：（1）根据定义，由_____________
的个数来判断；（2）根据性质，由____________________________的关系来判断。在实际应用中，常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r练一练1.已知圆的直径为13cm,如果直线和圆心的距离为:
1)4.5cm 2)6.5cm 3)8cm
那么直线和圆分别有几个公共点,为什么?3.圆中最大的弦长为10，如果直线与圆相交，设
直线与圆心的距离为d，则（ ）
（A）d＞10 （B）0＜d＜10
（C）d＞5 （D）0＜d＜5例题 在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm。BCA分析：要了解AB与⊙C的位置
关系，只要知道圆心C到AB的
距离d与r的关系。解：过C作CD⊥AB，垂足为D。在Rt△ABC中，AB= ==5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD= ==2.4（cm）。2222D4532.4cm思考：图中线段AB的长度
为多少？怎样求圆心C到直
线AB的距离？ 即圆心C到AB的距离d=2.4cm。（1）当r=2cm时， ∵d＞r，
∴⊙C与AB相离。（2）当r=2.4cm时，∵d=r，
∴⊙C与AB相切。（3）当r=3cm时， ∵d＜r，
∴⊙C与AB相交。ABCAD453d=2.4cm解：过C作CD⊥AB，垂足为D。在Rt△ABC中，AB= ==5（cm）根据三角形面积公式有CD·AB=AC·BC∴CD= ==2.4（cm）。2222在Rt△ABC中，∠C=90°，
AC=3cm，BC=4cm，
以C为圆心，r为半径的圆
与AB有怎样的位置关系？
为什么？（1）r=2cm；
（2）r=2.4cm (3)r=3cm。想一想2.已知⊙O的半径r=5cm,直线m上一点与圆心O的距离为5cm,则直线M和⊙O的位置关系为______.相交或相切3.已知如图,∠AOB=β(β为锐角),点E在OA上,
OE=5cm,以E为圆心,2.5cm为半径作圆
(1)⊙E与直线OB的位置关系由_____的大小决定.
(2)⊙E若与直线相切,则β=_________.
(3)⊙E若与直线相交,则β的取值范围为
β30°0°≤β＜30°4.圆心O到直线m的距离为d，⊙O半径为R，
若d、R是方程x2-9x+20=0的两个根，则直线
m和⊙O的位置关系为____________;若d、R
是方程X2-4x+m=0的两根,且直线m与⊙O相
切,则m的值为_______。想一想相交或相离4选择题：1、直线L上的一点到圆心O的距离等于⊙O的半径，则直线L与⊙O的位置关系是（ ）
（A）相离（B）相切（C）相交（D）相切或相交
2、已知等腰梯形ABCD上底AD长为3，下底BC长为11，一腰AB长为5，以A为圆心，AD为半径的圆与底BC的位置关系是（ ）
（A）相离（B）相交（C）相切（D）以上均错DC思考题：
已知△ABC中，∠B=30°，
∠A=15°BC=2，以A为圆心，r为
半径作圆A与BC相离，则r的取值
范围为______。小结：直线和圆的位置关系2
1
0
dd>r
交点切点无
割线 切线 无
谢谢指导