与圆的位置关系[上学期]
图片预览





文档简介
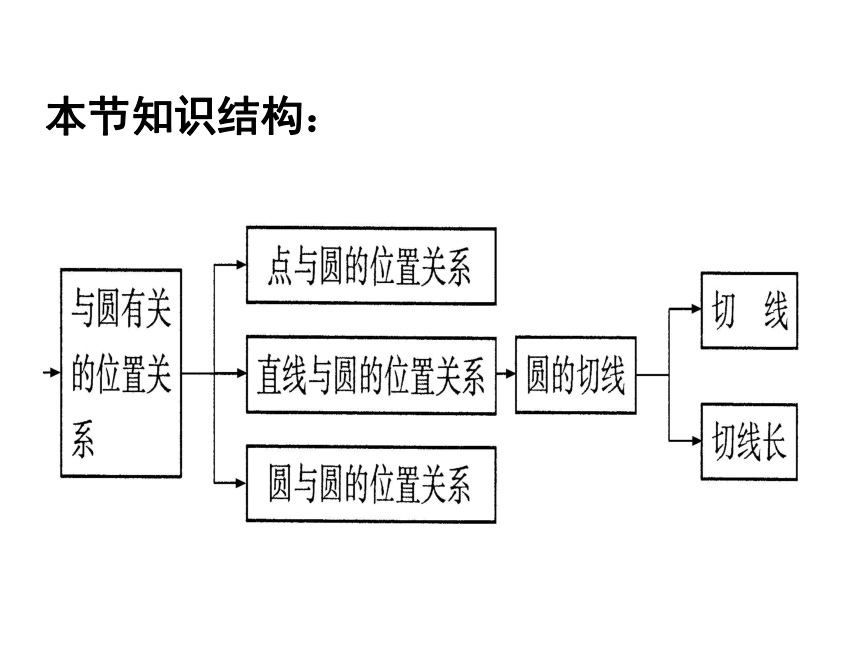
课件26张PPT。热烈欢迎各位莅临指导!洪泽外国语中学与圆有关的位置关系复习课本节知识结构: 1、已知圆P的半径为3,点Q在圆P外,点R在圆P上,点H在圆P内,则PQ___3,PR____3,PH_____3.你知道吗?点与圆的位置关系如图,设⊙O的半径为r,A点在圆内,B点在圆上,
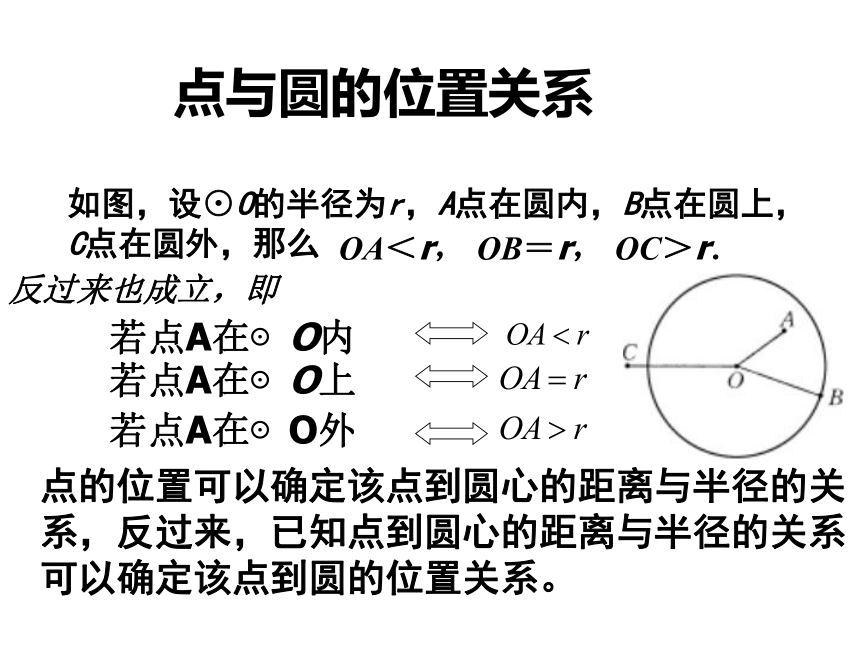
C点在圆外,那么OA<r, OB=r, OC>r.反过来也成立,即点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系。1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是______。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ____。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ______。 零相离直线和圆的位置关系图形公共点个数直线和圆的位置关系圆心到直线的
距离d与半径
r 的关系
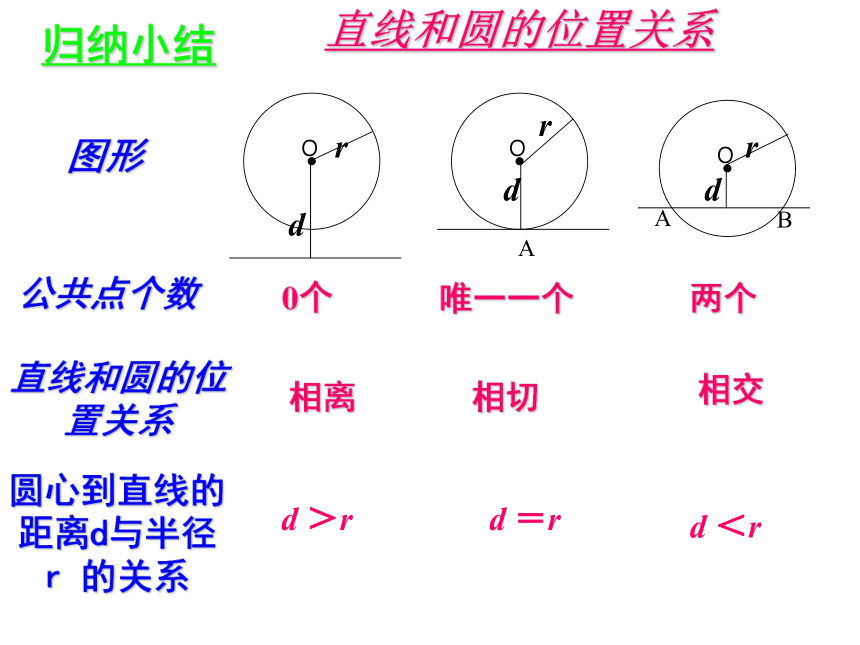
0个唯一一个两个相离相切相交d <rd =rd >r
AAB归纳小结问题
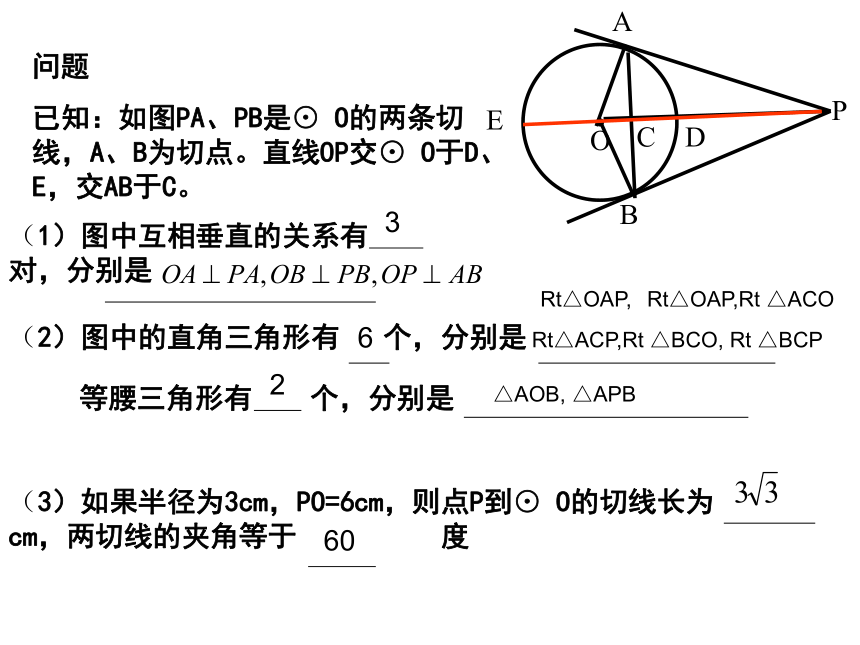
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。(2)图中的直角三角形有 个,分别是36260Rt△OAP,Rt△OAP,Rt △ACORt△ACP,Rt △BCO, Rt △BCP△AOB, △APB切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO∵PA、PB分别切⊙O于A、B,连结PO∴PA = PB,∠OPA=∠OPB
1、判断:
如图:1、△ABC是大圆O的外切三角形。( )
2、小圆O是△ABC的外接圆。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCO练习?
外心(三角形外接圆的圆心)
?
脑筋转转转1、若两圆有唯一公共点,且两圆半径分别为5和2,则两圆圆心距为 。思考:圆心A到X轴、
Y轴的距离各是多少? 2.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。 相离相切圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交d>R+rd=R+rd=R-r (R>r)R-rr)dr)本节知识结构: 问题1、如图已知直线AB过⊙O上的点C,并且
OA=OB,CA=CB 求证:直线AB是⊙O的切线证明:连接OC∵ OA=OB,CA=CB∴ OC是等腰三角形OAB底边AB上的中线∴ AB⊥OC直线AB经过半径OC的外端C,并且垂直于半径OC,所以AB是⊙O的切线问题2、如图:点O为∠ABC平分线上一点, OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。证明:作OE⊥BC于E∵ 点O为∠ABC平分线上一点
OD⊥AB于D∴ OE=OD又∵ OD为⊙O半径圆心O到直线BC的距离等于半径,所以BC与⊙O相切作OE⊥BC于E 当已知条件中没有明确直线与圆是否有公共点时 辅助线:是过圆心作这条 直线的垂线段。 再证明这条垂线段的长等于半径。连结OC 当已知条件中直线与圆已有一个公共点时 辅助线:是连结圆心和这 个公共点。再证明这条半径与直线垂直。 1、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC与作⊙O相切。
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
判断: 若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )请做随堂练习!AC×4、设⊙O的半径为r,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d与r的
关系是……………………( )
A、d≤r B、d<r C、d≥r D、d=rC练习(2)设⊙O与⊙ P内切于点B,
则
PB=OP+OB
∴ PB=13cm 5、 如图,⊙O的半径为5cm,点P是⊙ O外一点,
OP=8cm。求
(1)以P为圆心作⊙ P与⊙O外切,小圆⊙ P的半径是多少?
(2)以P为圆心作⊙ P与⊙O内切,大圆⊙ P的半径是多少?PABO解: (1)设⊙O与⊙ P外切于点A,
则
PA=OP-OA。
∴ PA=3cmAB7、已知⊙A、 ⊙ B相切,圆心距为10厘米,
其中⊙ A的半径为4厘米,求⊙ B的半径。6.如图,已知∠AOB=3Oo,M为OB上一点,以
M为圆心,2cm为半径作⊙M。若点M在OB上
运动,则当OM= cm时,⊙M与OA相切。
思考:OM满足什么条件时,⊙M与OA有两个公共点?
8、证明题:
(1)、如图:AB为⊙O直径,⊙O过BC中点D,
DE ⊥ AC 垂足为E
求证:DE是⊙O的切线练习本节课我们有什么收获?交流与反思感谢各位莅临指导洪泽外国语中学
C点在圆外,那么OA<r, OB=r, OC>r.反过来也成立,即点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系。1、已知⊙O的半径为5cm,O到
直线a的距离为3cm,则⊙O与直
线a的位置关系是_____。直线a
与⊙O的公共点个数是______。
2、已知⊙O的半径是4cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ____。动动脑筋相交 相切两个
3、已知⊙O的半径为6cm,O到
直线a的距离为7cm,则直线a与
⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,
O到直线a的距离是4cm,
则⊙O与直线a的位置关系是 ______。 零相离直线和圆的位置关系图形公共点个数直线和圆的位置关系圆心到直线的
距离d与半径
r 的关系
0个唯一一个两个相离相切相交d <rd =rd >r
AAB归纳小结问题
已知:如图PA、PB是⊙ O的两条切线,A、B为切点。直线OP交⊙ O于D、E,交AB于C。(2)图中的直角三角形有 个,分别是36260Rt△OAP,Rt△OAP,Rt △ACORt△ACP,Rt △BCO, Rt △BCP△AOB, △APB切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO∵PA、PB分别切⊙O于A、B,连结PO∴PA = PB,∠OPA=∠OPB
1、判断:
如图:1、△ABC是大圆O的外切三角形。( )
2、小圆O是△ABC的外接圆。 ( )
2、到三角形三边距离相等的点是三角形的( )
A、内心 B、外心
3、一个直角三角形的斜边的长为10cm,内切圆的半径为1cm,则三角形的周长是-------------- ABCO练习?
外心(三角形外接圆的圆心)
?
脑筋转转转1、若两圆有唯一公共点,且两圆半径分别为5和2,则两圆圆心距为 。思考:圆心A到X轴、
Y轴的距离各是多少? 2.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。 相离相切圆
和
圆
的
位
置
关
系外 离内 切相 交外 切内 含没有公共点相 离一个公共点相切两个公共点相交d>R+rd=R+rd=R-r (R>r)R-r
OA=OB,CA=CB 求证:直线AB是⊙O的切线证明:连接OC∵ OA=OB,CA=CB∴ OC是等腰三角形OAB底边AB上的中线∴ AB⊥OC直线AB经过半径OC的外端C,并且垂直于半径OC,所以AB是⊙O的切线问题2、如图:点O为∠ABC平分线上一点, OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC是⊙O 的切线。证明:作OE⊥BC于E∵ 点O为∠ABC平分线上一点
OD⊥AB于D∴ OE=OD又∵ OD为⊙O半径圆心O到直线BC的距离等于半径,所以BC与⊙O相切作OE⊥BC于E 当已知条件中没有明确直线与圆是否有公共点时 辅助线:是过圆心作这条 直线的垂线段。 再证明这条垂线段的长等于半径。连结OC 当已知条件中直线与圆已有一个公共点时 辅助线:是连结圆心和这 个公共点。再证明这条半径与直线垂直。 1、如图已知直线AB过⊙O上的点C,并且OA=OB,CA=CB
求证:直线AB是⊙O的切线2、如图:点O为∠ABC平分线上一点,OD⊥AB于D,以O为圆心,OD为半径作圆。 求证:BC与作⊙O相切。
1. ⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
判断: 若线段和圆没有公共点,该圆圆心到线段的距离大于半径. ( )请做随堂练习!AC×4、设⊙O的半径为r,点O到直线a的距离为d,
若⊙O与直线a至多只有一个公共点,则d与r的
关系是……………………( )
A、d≤r B、d<r C、d≥r D、d=rC练习(2)设⊙O与⊙ P内切于点B,
则
PB=OP+OB
∴ PB=13cm 5、 如图,⊙O的半径为5cm,点P是⊙ O外一点,
OP=8cm。求
(1)以P为圆心作⊙ P与⊙O外切,小圆⊙ P的半径是多少?
(2)以P为圆心作⊙ P与⊙O内切,大圆⊙ P的半径是多少?PABO解: (1)设⊙O与⊙ P外切于点A,
则
PA=OP-OA。
∴ PA=3cmAB7、已知⊙A、 ⊙ B相切,圆心距为10厘米,
其中⊙ A的半径为4厘米,求⊙ B的半径。6.如图,已知∠AOB=3Oo,M为OB上一点,以
M为圆心,2cm为半径作⊙M。若点M在OB上
运动,则当OM= cm时,⊙M与OA相切。
思考:OM满足什么条件时,⊙M与OA有两个公共点?
8、证明题:
(1)、如图:AB为⊙O直径,⊙O过BC中点D,
DE ⊥ AC 垂足为E
求证:DE是⊙O的切线练习本节课我们有什么收获?交流与反思感谢各位莅临指导洪泽外国语中学
