第6章 导数及其应用 章末综合提升 课件(共25张PPT)
文档属性
| 名称 | 第6章 导数及其应用 章末综合提升 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 11:16:59 | ||
图片预览








文档简介
(共25张PPT)
章末综合提升
第六章 导数及其应用
巩固层·知识整合
01
提升层·题型探究
02
类型1
类型2
类型3
类型4
点击右图进入…
章
末
综
合
测
评
谢谢观看 THANK YOU!
浅仰芹
我仰
h
团结守纪勤学春
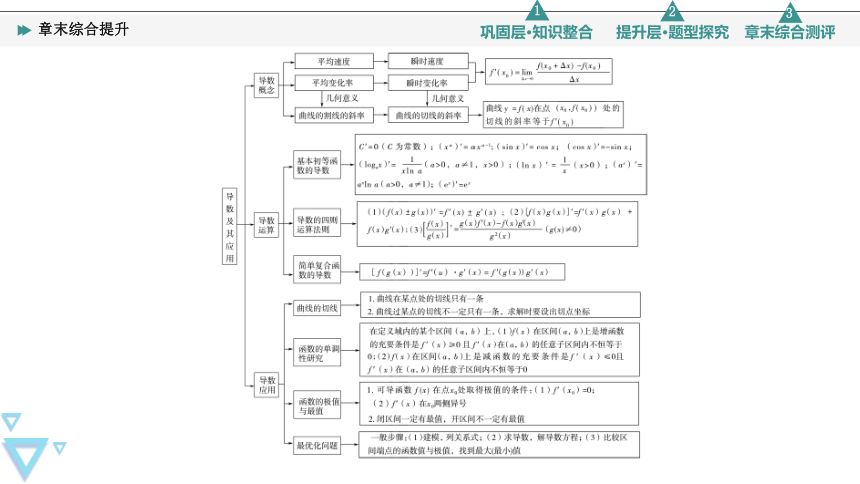
平均速度
瞬时速度
f(xo+△x)-fxo)
f()=lim
导数
△x0
平均变化率
瞬时变化率
△x
概念
几何意义
几何意义
曲线y=f(x)在点(xo,f(xo)处的
曲线的割线的斜率
曲线的切线的斜率
切线的斜率等于∫'(x)
C'=0(C为常数);(xm)'=x-1l;(sinx)'=cosx;(cosx)'=-sinx;
基本初等函
数的导数
(1gr=(o>0,a≠1,>0):(n)'=(x>0);()=
xIn a
2
a*lna(a>0,a≠1);(e*)'=e
数及其应用
(1)(f(x)±g(x)′=f'(x)±g'(x);(2)f(x)g(x)]'f'(x)g(x)+
导数
导数的四则
运算
运算法则
fe 3-re
g2(x)
(g(x)≠0)
简单复合函
数的导数
[f(g(x))]'f'(u)·g'(x)=f'(g(x)g'(x)
1.曲线在某点处的切线只有一条
曲线的切线
2.曲线过某点的切线不一定只有一条,求解时要设出切点坐标
在定义域内的某个区间(a,b)上,(1)f(x)在区间(a,b)上是增函数
函数的单调
的充要条件是f'(x)≥0且f'(x)在(a,b)的任意子区间内不恒等于
性研究
0;(2)f(x)在区间(a,b)上是减函数的充要条件是f'(x)≤0且
f'(x)在(a,b)的任意子区间内不恒等于0
导数
应用
1.可导函数f(x)在点xo处取得极值的条件:(1)f(xo)=0;
函数的极值
(2)f(x)在x两侧异号
与最值
2.闭区间一定有最值,开区间不一定有最值
般步骤:(1)建模,列关系式;(2)求导数,解导数方程;(3)比较区
最优化问题
间端点的函数值与极值,找到最大(最小)值
W
章末综合提升
第六章 导数及其应用
巩固层·知识整合
01
提升层·题型探究
02
类型1
类型2
类型3
类型4
点击右图进入…
章
末
综
合
测
评
谢谢观看 THANK YOU!
浅仰芹
我仰
h
团结守纪勤学春
平均速度
瞬时速度
f(xo+△x)-fxo)
f()=lim
导数
△x0
平均变化率
瞬时变化率
△x
概念
几何意义
几何意义
曲线y=f(x)在点(xo,f(xo)处的
曲线的割线的斜率
曲线的切线的斜率
切线的斜率等于∫'(x)
C'=0(C为常数);(xm)'=x-1l;(sinx)'=cosx;(cosx)'=-sinx;
基本初等函
数的导数
(1gr=(o>0,a≠1,>0):(n)'=(x>0);()=
xIn a
2
a*lna(a>0,a≠1);(e*)'=e
数及其应用
(1)(f(x)±g(x)′=f'(x)±g'(x);(2)f(x)g(x)]'f'(x)g(x)+
导数
导数的四则
运算
运算法则
fe 3-re
g2(x)
(g(x)≠0)
简单复合函
数的导数
[f(g(x))]'f'(u)·g'(x)=f'(g(x)g'(x)
1.曲线在某点处的切线只有一条
曲线的切线
2.曲线过某点的切线不一定只有一条,求解时要设出切点坐标
在定义域内的某个区间(a,b)上,(1)f(x)在区间(a,b)上是增函数
函数的单调
的充要条件是f'(x)≥0且f'(x)在(a,b)的任意子区间内不恒等于
性研究
0;(2)f(x)在区间(a,b)上是减函数的充要条件是f'(x)≤0且
f'(x)在(a,b)的任意子区间内不恒等于0
导数
应用
1.可导函数f(x)在点xo处取得极值的条件:(1)f(xo)=0;
函数的极值
(2)f(x)在x两侧异号
与最值
2.闭区间一定有最值,开区间不一定有最值
般步骤:(1)建模,列关系式;(2)求导数,解导数方程;(3)比较区
最优化问题
间端点的函数值与极值,找到最大(最小)值
W
