【新课标】6.1.1 平行四边形的性质 课件(共23张PPT)
文档属性
| 名称 | 【新课标】6.1.1 平行四边形的性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 13:50:23 | ||
图片预览




文档简介
(共23张PPT)
6.1.1 平行四边形的性质
北师版八年级下册
教学目标
1.理解平行四边形的定义及有关概念.
2.能根据定义探索并掌握平行四边形的对边相等、对角相等的性质.
新知导入
请同学们观察图片,你能找出图形里面的平行四边形吗?
探究新知
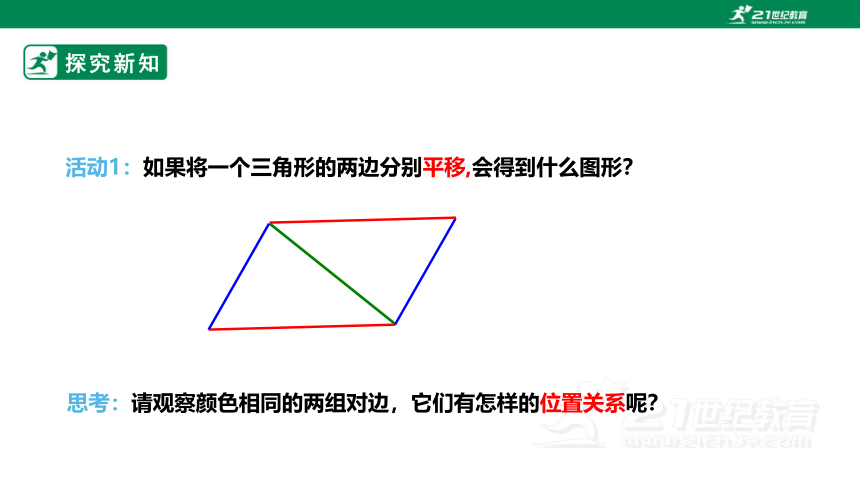
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
探究新知
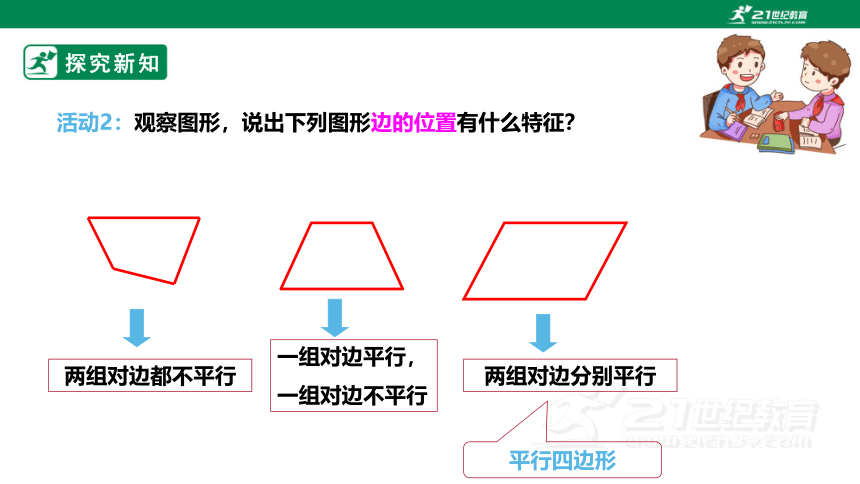
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
归纳总结
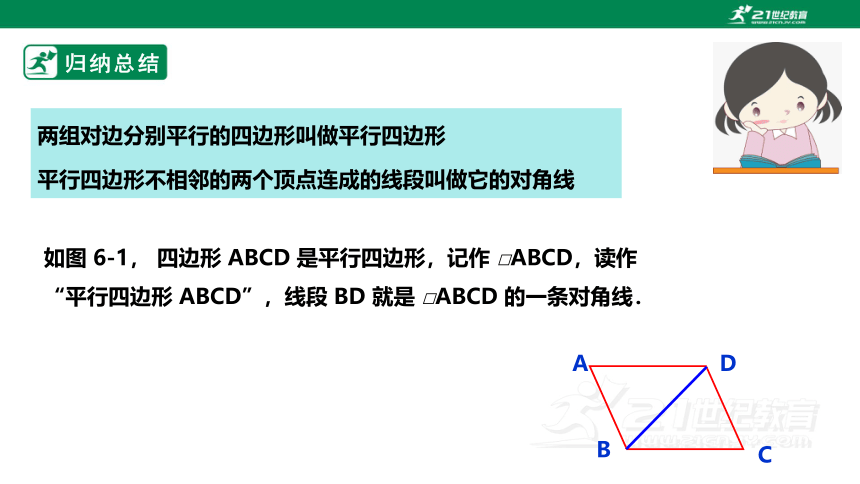
两组对边分别平行的四边形叫做平行四边形
平行四边形不相邻的两个顶点连成的线段叫做它的对角线
如图 6-1, 四边形 ABCD 是平行四边形,记作 □ABCD,读作 “平行四边形 ABCD”,线段 BD 就是 □ABCD 的一条对角线.
A
B
C
D
做一做
(1)平行四边形是中心对称图形吗?如果是,你能找出它的对称中心并验证你的结论吗?
(2)你还发现平行四边形有哪些性质?
性质2:平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对边相等、对角相等.
能否证明这些结论?
探究新知
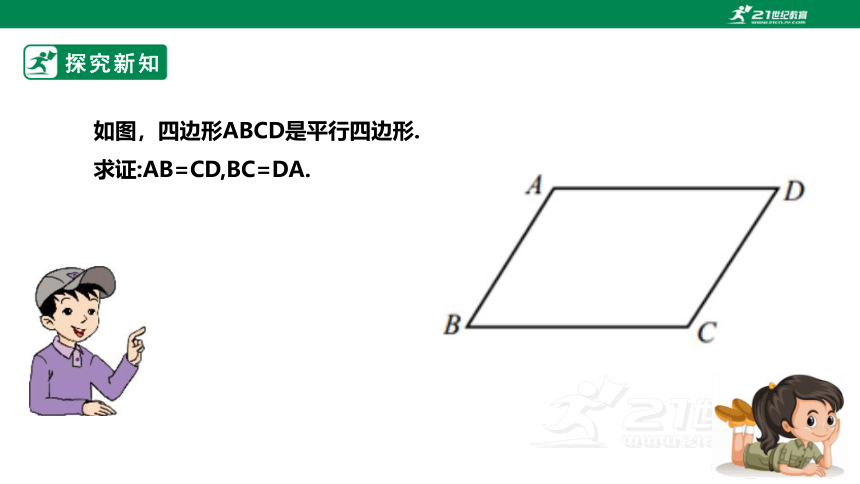
如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
探究新知
1
2
3
4
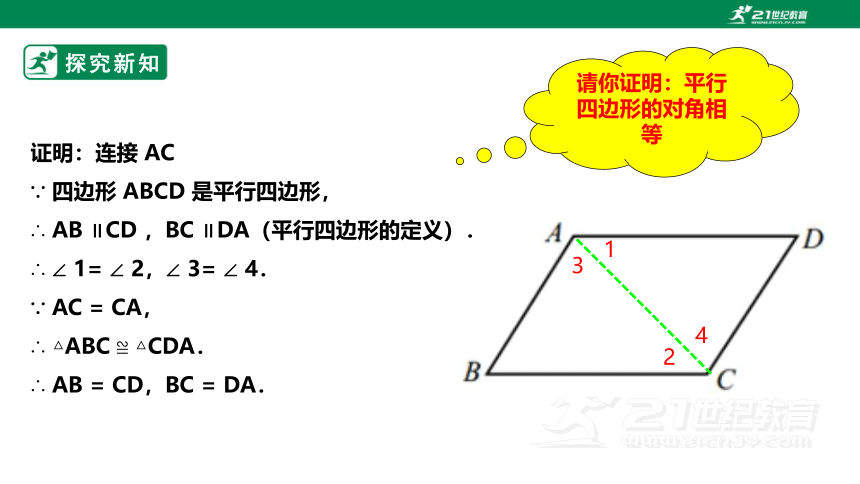
证明:连接 AC
∵ 四边形 ABCD 是平行四边形,
∴ AB ∥CD ,BC ∥DA(平行四边形的定义).
∴ ∠ 1= ∠ 2,∠ 3= ∠ 4.
∵ AC = CA,
∴ △ABC ≌ △CDA.
∴ AB = CD,BC = DA.
请你证明:平行四边形的对角相等
探究新知
证明:如图,连接AC,
∵四边形ABCD是平行四边形,
∴AD∥BC ,AB∥CD.
∴∠BAD+∠B=180° ,
∠BCD+∠B=180° .
∴∠BAD=∠BCD.同理∠B=∠D.
已知:四边形ABCD是平行四边形,求证:∠A=∠C,∠B=∠D
归纳总结
定理 平行四边形的对边相等.
定理 平行四边形的对角相等.
典例精析
例1、已知:如图,在平行四边形ABCD中,E,F 是对角线AC上的两点,且AE=CF.求证:BE = DF.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的定义).
∴ ∠BAE=∠DCF.
又∵ AE= CF,
∴ △ABE ≌ △CDF.
∴ BE = DF.
练一练
如图,四边形ABCD是平行四边形. 求:
(1) ∠ADC和∠BCD的度数;
(2) AB和BC的长度.
解:(1)因为∠B=56°,且平行四边形的对角相等,邻角互补,
所以∠ADC=56°,
∠BCD=180°-56°=124°.
(2)因为CD=25,AD=30,
且平行四边形的对边相等,
所以AB=25,BC=30.
课堂练习
1.在 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160°
C.80° D.60°
2.如图,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A.B.2 C.2 D.4
C
C
课堂练习
3、如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为______.
4.如图,在 ABCD 中,CE⊥AB,E 为垂足,如果∠A=120°,则∠BCE 的度数是 。
47°
30°
课堂练习
5.如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC=90°.
在△DEA和△BFC中,,
∴△DEA≌△BFC(AAS).
∴AE=CF.
课堂练习
6.如图,在 ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE ≌△FCE ;
(2)若AB=2BC,∠F=36°.求∠B的度数.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.∴∠D=∠ECF.
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA).
课堂练习
(2)解:∵△ADE≌△FCE,∴AD=FC.
∵AD=BC,∴FB=2BC.
又∵AB=2BC,∴AB=FB.
∴∠BAF=∠F=36°.
∴∠B=180°-2×36°=108°.
课堂总结
平行四边形
两组对边分别平行的四边形是平行四边形
定义
性质
对边平行,
对边相等,
对角相等
板书设计
课题:6.1.1平行四边形的性质
1、定义
2、性质
(1)边
(2)角
作业布置
【必做题】
教材137页练习题1、2题
【选做题】
教材137页练习题3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.1.1 平行四边形的性质
北师版八年级下册
教学目标
1.理解平行四边形的定义及有关概念.
2.能根据定义探索并掌握平行四边形的对边相等、对角相等的性质.
新知导入
请同学们观察图片,你能找出图形里面的平行四边形吗?
探究新知
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
探究新知
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
归纳总结
两组对边分别平行的四边形叫做平行四边形
平行四边形不相邻的两个顶点连成的线段叫做它的对角线
如图 6-1, 四边形 ABCD 是平行四边形,记作 □ABCD,读作 “平行四边形 ABCD”,线段 BD 就是 □ABCD 的一条对角线.
A
B
C
D
做一做
(1)平行四边形是中心对称图形吗?如果是,你能找出它的对称中心并验证你的结论吗?
(2)你还发现平行四边形有哪些性质?
性质2:平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
平行四边形的对边相等、对角相等.
能否证明这些结论?
探究新知
如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
探究新知
1
2
3
4
证明:连接 AC
∵ 四边形 ABCD 是平行四边形,
∴ AB ∥CD ,BC ∥DA(平行四边形的定义).
∴ ∠ 1= ∠ 2,∠ 3= ∠ 4.
∵ AC = CA,
∴ △ABC ≌ △CDA.
∴ AB = CD,BC = DA.
请你证明:平行四边形的对角相等
探究新知
证明:如图,连接AC,
∵四边形ABCD是平行四边形,
∴AD∥BC ,AB∥CD.
∴∠BAD+∠B=180° ,
∠BCD+∠B=180° .
∴∠BAD=∠BCD.同理∠B=∠D.
已知:四边形ABCD是平行四边形,求证:∠A=∠C,∠B=∠D
归纳总结
定理 平行四边形的对边相等.
定理 平行四边形的对角相等.
典例精析
例1、已知:如图,在平行四边形ABCD中,E,F 是对角线AC上的两点,且AE=CF.求证:BE = DF.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AB=CD(平行四边形的对边相等),
AB∥CD(平行四边形的定义).
∴ ∠BAE=∠DCF.
又∵ AE= CF,
∴ △ABE ≌ △CDF.
∴ BE = DF.
练一练
如图,四边形ABCD是平行四边形. 求:
(1) ∠ADC和∠BCD的度数;
(2) AB和BC的长度.
解:(1)因为∠B=56°,且平行四边形的对角相等,邻角互补,
所以∠ADC=56°,
∠BCD=180°-56°=124°.
(2)因为CD=25,AD=30,
且平行四边形的对边相等,
所以AB=25,BC=30.
课堂练习
1.在 ABCD中,∠A+∠C=200°,则∠B的度数是( )
A.100° B.160°
C.80° D.60°
2.如图,在 ABCD中,连接AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
A.B.2 C.2 D.4
C
C
课堂练习
3、如图,在 ABCD中,∠C=43°,过点D作AD的垂线,交AB于点E,交CB的延长线于点F,则∠BEF的度数为______.
4.如图,在 ABCD 中,CE⊥AB,E 为垂足,如果∠A=120°,则∠BCE 的度数是 。
47°
30°
课堂练习
5.如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC=90°.
在△DEA和△BFC中,,
∴△DEA≌△BFC(AAS).
∴AE=CF.
课堂练习
6.如图,在 ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
(1)求证:△ADE ≌△FCE ;
(2)若AB=2BC,∠F=36°.求∠B的度数.
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.∴∠D=∠ECF.
在△ADE和△FCE中,,
∴△ADE≌△FCE(ASA).
课堂练习
(2)解:∵△ADE≌△FCE,∴AD=FC.
∵AD=BC,∴FB=2BC.
又∵AB=2BC,∴AB=FB.
∴∠BAF=∠F=36°.
∴∠B=180°-2×36°=108°.
课堂总结
平行四边形
两组对边分别平行的四边形是平行四边形
定义
性质
对边平行,
对边相等,
对角相等
板书设计
课题:6.1.1平行四边形的性质
1、定义
2、性质
(1)边
(2)角
作业布置
【必做题】
教材137页练习题1、2题
【选做题】
教材137页练习题3、4题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
