函数及其表示(浙江省嘉兴市嘉善县)
文档属性
| 名称 | 函数及其表示(浙江省嘉兴市嘉善县) |

|
|
| 格式 | rar | ||
| 文件大小 | 43.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-19 17:55:00 | ||
图片预览



文档简介
课件11张PPT。函数的表示及映射复习回顾:
函数三种表示方法及各自的优点?解析法:全面,简明地表示了变量间的关系,可以通过解析式求出任意自变量所对应的函数值
列表法:不必计算就可以看出与自变量相所对应的函数值
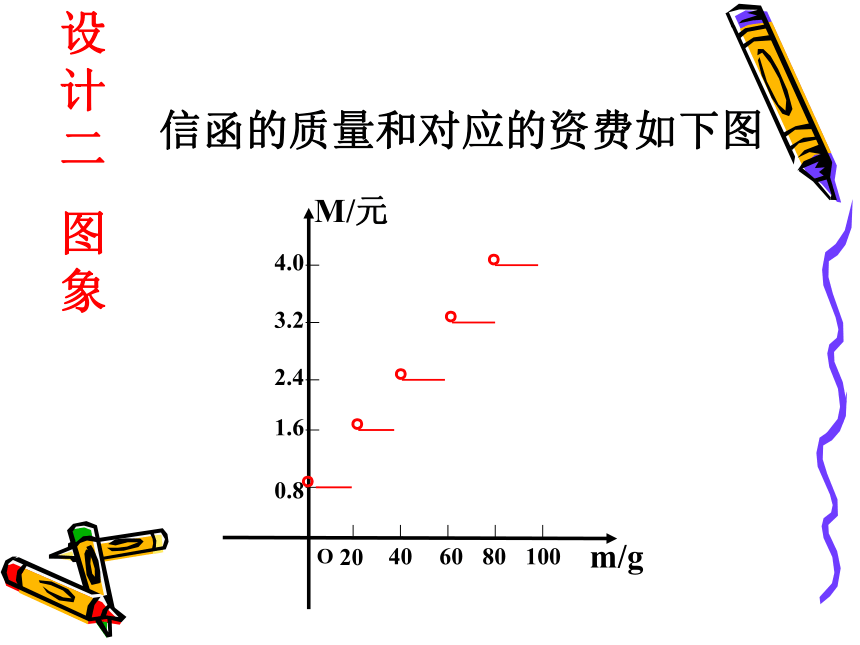
图象法:直观形象地表示自变量的变化,相应的函数值变化趋势.例1:某地投寄外地信函的收费标准:每封信函不超过20g付邮资0.80元,超过20g,而不超过40g付邮资1.60元.依次类推,每封信函超过100g不再按信函方式投寄,请你设计一个投寄以上信函的邮政资费示意牌,明确显示邮政资费标准.信函质量(m)/g邮资(M)/元0.801.602.403.204.00设计一:每封信函的质量和对应的资费如下表:20M/元m/g4060801000.81.62.43.24.0。。。。。设计二
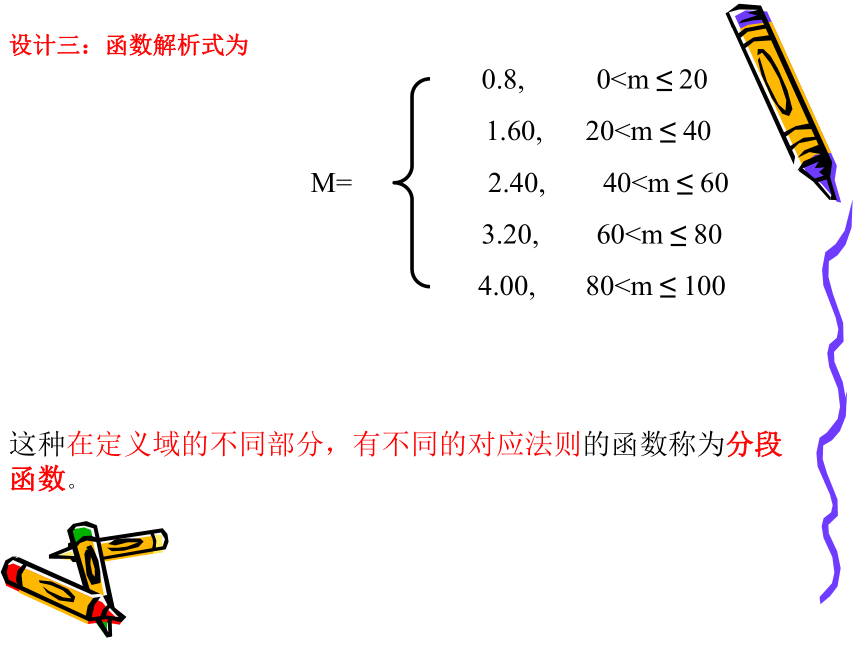
图象信函的质量和对应的资费如下图O这种在定义域的不同部分,有不同的对应法则的函数称为分段函数。设计三:函数解析式为1. 分段函数是一个函数,不要把它误认为是“几个函数”;2. 有些函数既可用列表法表示,也可用图像法或解析法表示.注意3.分段函数的定义域是各段定义域的并集。值域是各段值域的并集。4.分段函数在定义域的不同部分有不同的对应法则,
但它是一个函数习题:
(1)f(x)=2x x≥0x(x+1)x<0 则f(-2)=( )A.1 B.2 C.3 D.4(2)已知函数f(x)=2x x>2则f(2)=_____________若f(x0)=8,则x0=_____实例分析 1.集合A={全班同学},
集合B={全班同学的姓},
对应关系f:每一个同学对应属于自己的姓.2.集合A={中国,美国,英国,日本},B={北京,东京,华盛顿,伦敦},
对应关系f:每一个国家对应它的首都.3.设集合A={1,-3,2,3,-1,-2},
集合B={9,0,4,1,5},
对应关系f:每一个数对应它的平方数.三个对应的共同特点:(1)集合A中的每一个元素在集合B中都有对应元素;映射的概念(2)对于集合A中的每一个元素在集合B中的对应元素是唯一的.设A,B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射思考:在我们的生活中,有很多映射的例子,你能举出几个吗?思考:函数与映射有什么区别和联系?例3:以下给出的对应是不是从集合A到集合B的映射?(1)集合A={P|P是数轴上的点},集合B=R,
对应关系f:数轴上的点与它所代表的实数对应;(2)集合A={P|P是平面直角坐标系中的点},
集合B={(x,y)|x∈R,y∈R},
对应关系f:平面直角坐标系中的点与它的坐标对应;(3)集合A={x|x是三角形},集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内切圆(4)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生例4.设集合A={1,2,3,k},B={4,7,a4,a2+3a},其中a,k∈N,映射f:A→B,使B中元素y=3x+1与A中元素x对应,求a及k的值. (4)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生
若将对应关系f改为:每一个学生都对应它的班级,那么对应f:B→A是从集合B到A的映射吗?思考?
列表法:不必计算就可以看出与自变量相所对应的函数值
图象法:直观形象地表示自变量的变化,相应的函数值变化趋势.例1:某地投寄外地信函的收费标准:每封信函不超过20g付邮资0.80元,超过20g,而不超过40g付邮资1.60元.依次类推,每封信函超过100g不再按信函方式投寄,请你设计一个投寄以上信函的邮政资费示意牌,明确显示邮政资费标准.信函质量(m)/g邮资(M)/元0.801.602.403.204.00设计一:每封信函的质量和对应的资费如下表:20M/元m/g4060801000.81.62.43.24.0。。。。。设计二
图象信函的质量和对应的资费如下图O这种在定义域的不同部分,有不同的对应法则的函数称为分段函数。设计三:函数解析式为1. 分段函数是一个函数,不要把它误认为是“几个函数”;2. 有些函数既可用列表法表示,也可用图像法或解析法表示.注意3.分段函数的定义域是各段定义域的并集。值域是各段值域的并集。4.分段函数在定义域的不同部分有不同的对应法则,
但它是一个函数习题:
(1)f(x)=2x x≥0x(x+1)x<0 则f(-2)=( )A.1 B.2 C.3 D.4(2)已知函数f(x)=2x x>2则f(2)=_____________若f(x0)=8,则x0=_____实例分析 1.集合A={全班同学},
集合B={全班同学的姓},
对应关系f:每一个同学对应属于自己的姓.2.集合A={中国,美国,英国,日本},B={北京,东京,华盛顿,伦敦},
对应关系f:每一个国家对应它的首都.3.设集合A={1,-3,2,3,-1,-2},
集合B={9,0,4,1,5},
对应关系f:每一个数对应它的平方数.三个对应的共同特点:(1)集合A中的每一个元素在集合B中都有对应元素;映射的概念(2)对于集合A中的每一个元素在集合B中的对应元素是唯一的.设A,B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有惟一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射思考:在我们的生活中,有很多映射的例子,你能举出几个吗?思考:函数与映射有什么区别和联系?例3:以下给出的对应是不是从集合A到集合B的映射?(1)集合A={P|P是数轴上的点},集合B=R,
对应关系f:数轴上的点与它所代表的实数对应;(2)集合A={P|P是平面直角坐标系中的点},
集合B={(x,y)|x∈R,y∈R},
对应关系f:平面直角坐标系中的点与它的坐标对应;(3)集合A={x|x是三角形},集合B={x|x是圆},
对应关系f:每一个三角形都对应它的内切圆(4)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生例4.设集合A={1,2,3,k},B={4,7,a4,a2+3a},其中a,k∈N,映射f:A→B,使B中元素y=3x+1与A中元素x对应,求a及k的值. (4)集合A={x|x是新华中学的班级},
集合B={x|x是新华中学的学生},
对应关系f:每一个班级都对应班里的学生
若将对应关系f改为:每一个学生都对应它的班级,那么对应f:B→A是从集合B到A的映射吗?思考?
