函数的单调性(浙江省嘉兴市嘉善县)
文档属性
| 名称 | 函数的单调性(浙江省嘉兴市嘉善县) |

|
|
| 格式 | rar | ||
| 文件大小 | 173.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-17 00:00:00 | ||
图片预览

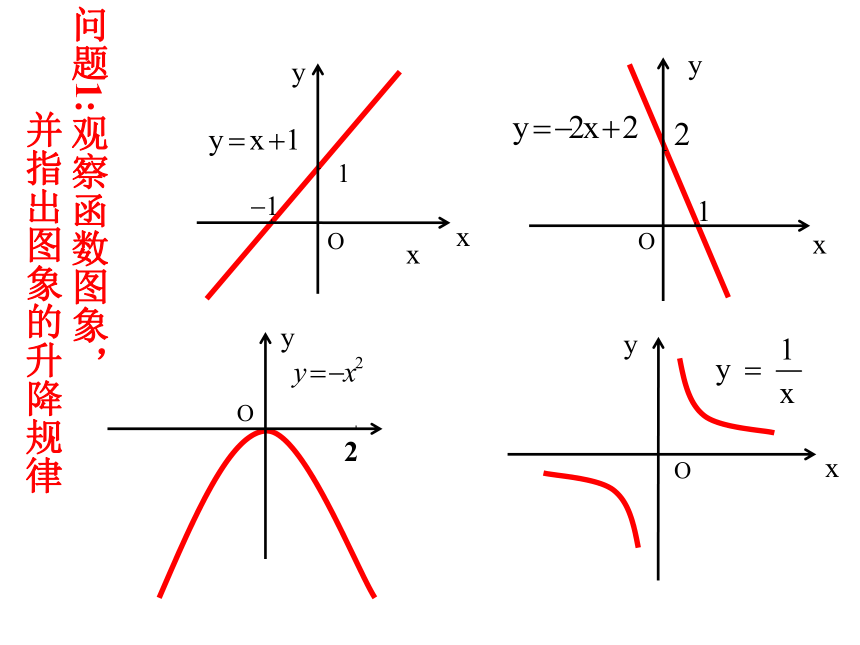

文档简介
课件20张PPT。 函数的单调性
浙江省嘉善中学
刘胡礼
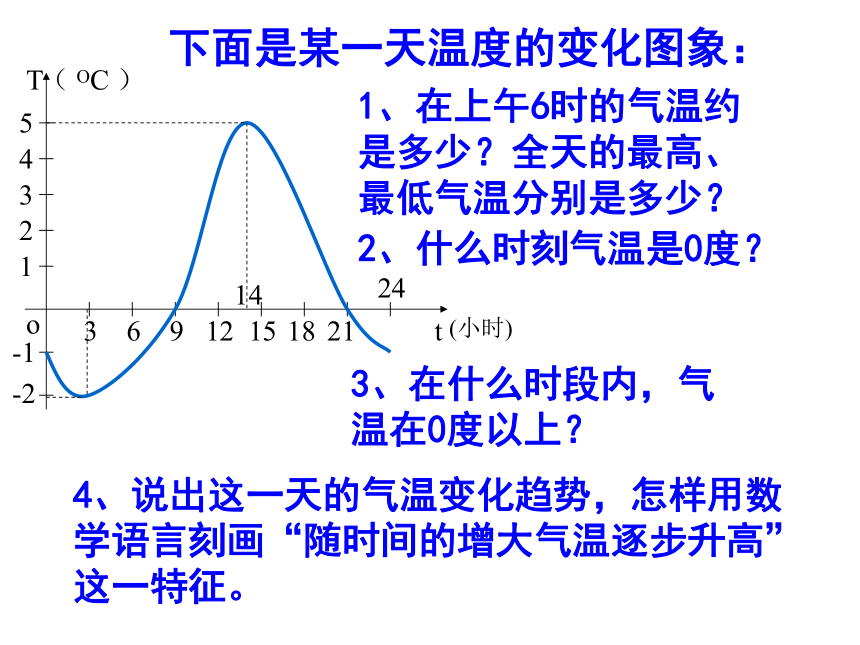
引入下面是某一天温度的变化图象:1、在上午6时的气温约是多少?全天的最高、最低气温分别是多少?2、什么时刻气温是0度?3、在什么时段内,气温在0度以上?4、说出这一天的气温变化趋势,怎样用数学语言刻画“随时间的增大气温逐步升高”这一特征。Oxy2问题1:观察函数图象,
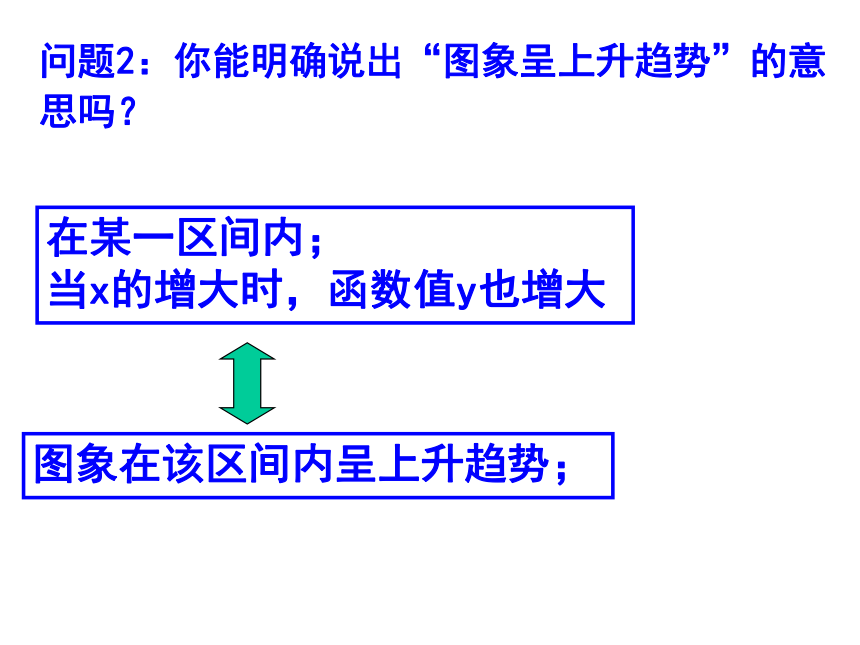
并指出图象的升降规律问题2:你能明确说出“图象呈上升趋势”的意思吗?在某一区间内;
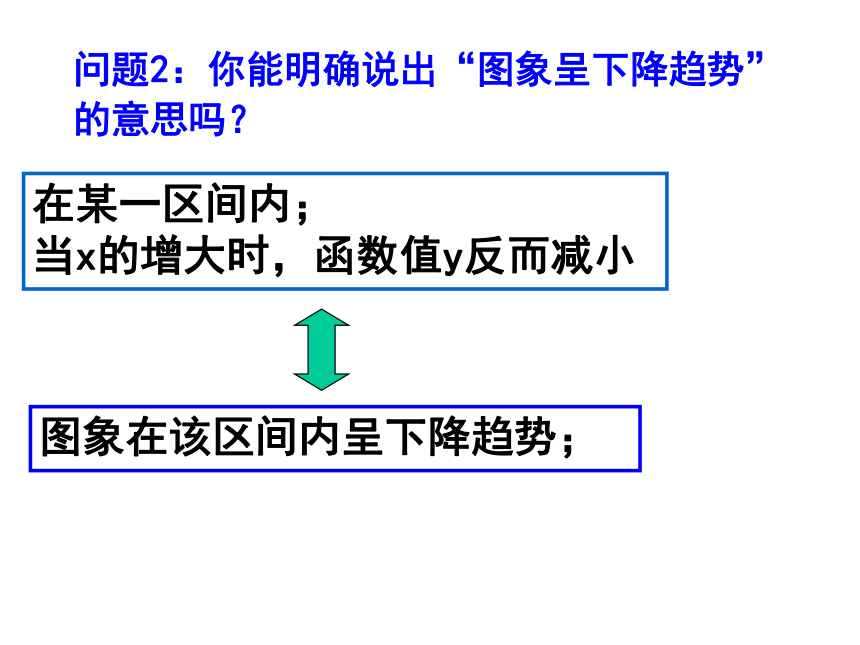
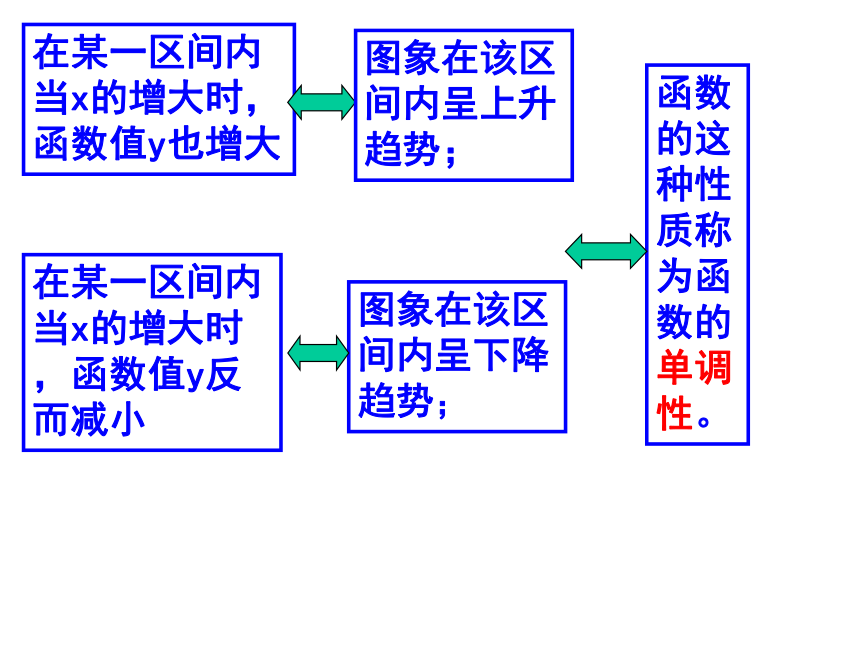
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;问题2:你能明确说出“图象呈下降趋势”的意思吗?在某一区间内;
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
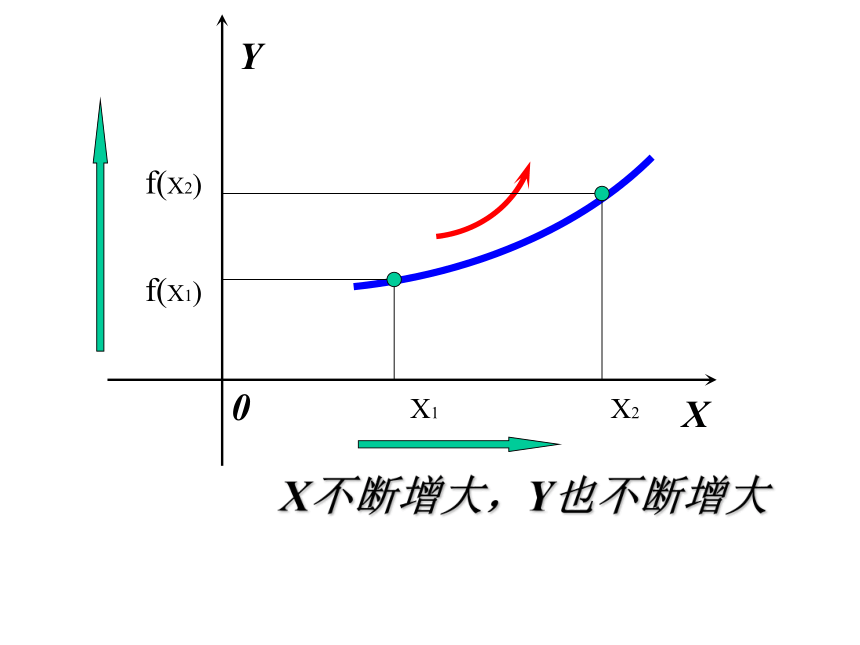
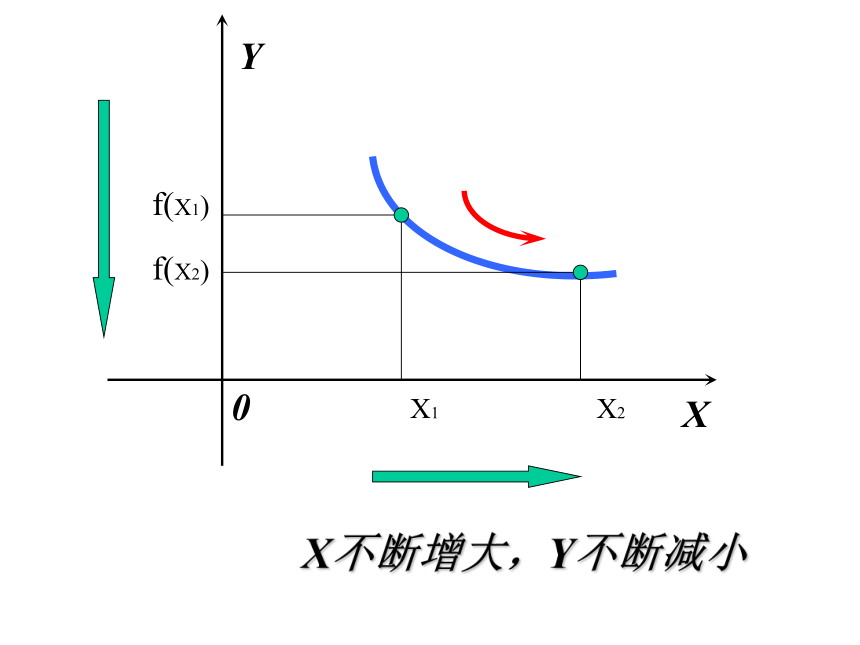
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;函数的这种性质称为函数的单调性。 X不断增大,Y也不断增大0 XYX1X2f(X1)f(X2)Y X0 X不断增大,Y不断减小X1X2f(X2)f(X1)函数f (x)在给定区间上为增函数。如何用x与 f(x)数值的变化来描述上升的图象?如何用x与 f(x)数值的变化来描述下降的图象?函数f (x)在给定区间上为减函数。如果对于属于定义域I内的某个区间D上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)< f(x2),那么就说f(x).在区间D上是增函数.D就叫做函数f(x)的增区间.增函数与减函数定义思考1、x1,x2是在整个定义域上取值吗?如果不是,是在哪儿?思考2、x1,x2是取特殊值吗?若不是,应该是取什么样的值?思考3、能说在整个定义域上是增函数吗?
若不能,应怎么说?思考4、定义中的“都有”能去掉吗?请举例说明思考5、你是怎么理解“任意”的?如果对于属于定义域I内的某个区间D上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)> f(x2),那么就说f(x) .在D上是减函数. D就叫做函数f(x)的减区间思考1、x1,x2是在整个定义域上取值吗?如果不是,是在哪儿?思考2、x1,x2是取特殊值吗?若不是,应该是取什么样的值?思考3、能说在整个定义域上是减函数吗?
若不能,应怎么说?思考4、定义中的“都有”能去掉吗?请举例说明思考5、你是怎么理解“任意”的?说明1函数y=f(x)在区间D上是增函数或减函数,就称函数y=f(x)在区间D上具有单调性,
D称为函数的单调区间。例1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-3),[-3,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一.单调递增区间:单调递减区间:25讨论二次函数y=ax2+bx+c(a≠0)的单调性。 当a>0时,函数y=ax2+bx+c(a≠0)在
上为减函数,在 上为增函数; 当a<0时,函数y=ax2+bx+c(a≠0)在
上为增函数,在 上为减函数;证明:(条件)(论证结果)(结论)例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1减函数例2:证明函数f(x)=1/x在区间(0,+∞)上是增函数还是减函数?并证明你的结论。x1x2y1y2x2x1y1y2小结:解:函数f(x)=x2+1在(0,+∞)上是增函数.下面给予证明:设x1,x2∈(0,+∞),且x1<x2∴函数f(x)=x2+1在(0,+∞)上是增函数.例3:证明函数f(x)=x2+1在区间(0,+∞)上是增函数还是减函数?并给予证明。
浙江省嘉善中学
刘胡礼
引入下面是某一天温度的变化图象:1、在上午6时的气温约是多少?全天的最高、最低气温分别是多少?2、什么时刻气温是0度?3、在什么时段内,气温在0度以上?4、说出这一天的气温变化趋势,怎样用数学语言刻画“随时间的增大气温逐步升高”这一特征。Oxy2问题1:观察函数图象,
并指出图象的升降规律问题2:你能明确说出“图象呈上升趋势”的意思吗?在某一区间内;
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;问题2:你能明确说出“图象呈下降趋势”的意思吗?在某一区间内;
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
当x的增大时,函数值y反而减小图象在该区间内呈下降趋势;在某一区间内
当x的增大时,函数值y也增大图象在该区间内呈上升趋势;函数的这种性质称为函数的单调性。 X不断增大,Y也不断增大0 XYX1X2f(X1)f(X2)Y X0 X不断增大,Y不断减小X1X2f(X2)f(X1)函数f (x)在给定区间上为增函数。如何用x与 f(x)数值的变化来描述上升的图象?如何用x与 f(x)数值的变化来描述下降的图象?函数f (x)在给定区间上为减函数。如果对于属于定义域I内的某个区间D上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)< f(x2),那么就说f(x).在区间D上是增函数.D就叫做函数f(x)的增区间.增函数与减函数定义思考1、x1,x2是在整个定义域上取值吗?如果不是,是在哪儿?思考2、x1,x2是取特殊值吗?若不是,应该是取什么样的值?思考3、能说在整个定义域上是增函数吗?
若不能,应怎么说?思考4、定义中的“都有”能去掉吗?请举例说明思考5、你是怎么理解“任意”的?如果对于属于定义域I内的某个区间D上的任意两个自变量的值x1 、x2,当x1<x2时,都有f(x1)> f(x2),那么就说f(x) .在D上是减函数. D就叫做函数f(x)的减区间思考1、x1,x2是在整个定义域上取值吗?如果不是,是在哪儿?思考2、x1,x2是取特殊值吗?若不是,应该是取什么样的值?思考3、能说在整个定义域上是减函数吗?
若不能,应怎么说?思考4、定义中的“都有”能去掉吗?请举例说明思考5、你是怎么理解“任意”的?说明1函数y=f(x)在区间D上是增函数或减函数,就称函数y=f(x)在区间D上具有单调性,
D称为函数的单调区间。例1:下图是定义在[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一单调区间上, y=f(x)是增函数还是减函数.解:y=f(x)的单调区间有[-5,-3),[-3,1)[1,3),[3,5].其中y=f(x)在[-5,-2), [1,3)上是减函数,在[-2,1), [3,5)上是增函数.作图是发现函数单调性的方法之一.单调递增区间:单调递减区间:25讨论二次函数y=ax2+bx+c(a≠0)的单调性。 当a>0时,函数y=ax2+bx+c(a≠0)在
上为减函数,在 上为增函数; 当a<0时,函数y=ax2+bx+c(a≠0)在
上为增函数,在 上为减函数;证明:(条件)(论证结果)(结论)例1:证明函数f(x)=2x+1在区间(-∞,+∞)上是增函数。证明函数单调性的步骤:第一步:取值.即任取区间内的两个值,且x1
