复习第三章(江苏省徐州市鼓楼区)

课件18张PPT。复习第三章

用字母表示数 一、基本考点：
1.某商品售价m元,打7折后又降价40元,则
现价为 元.
2.对于代数式“5 ”，我们可以这样来解释：
某人以5千米∕时的速度走了 小时，他
一共走的路程是5 千米. 请你对代数式
“2a+2b”给出一个具有实际意义的解释：
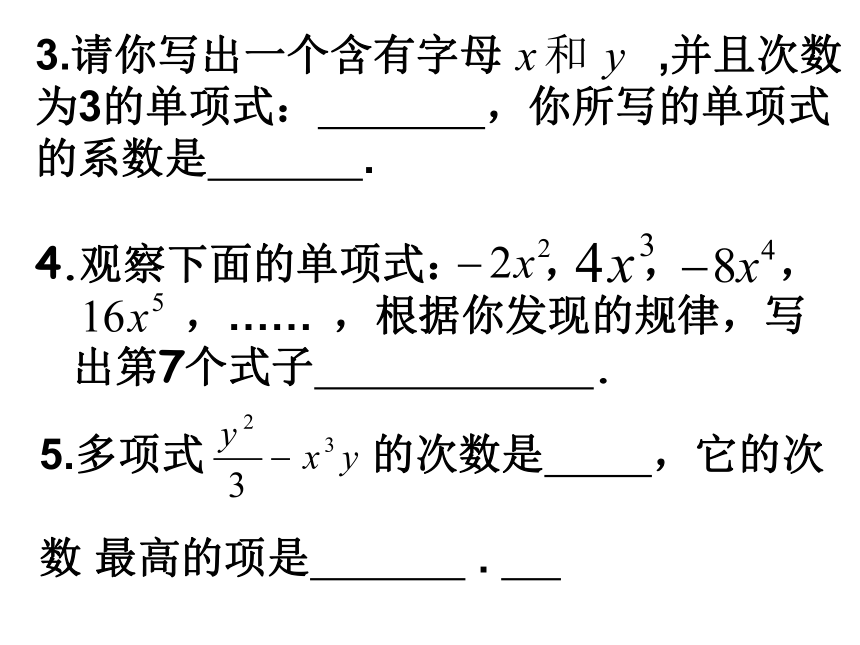
.(0.7m-40)3.请你写出一个含有字母 ,并且次数
为3的单项式： ，你所写的单项式
的系数是 .
4.观察下面的单项式： ， ， ，
，…… ，根据你发现的规律，写
出第7个式子 .
5.多项式 的次数是 ，它的次
数 最高的项是 . 6.下列各式中，正确的是（ ）
A. x- (2y - z)= x – 2y – z
B. 3a - 2(a-b) = 3a - 2a + b
C. a2+b2 - 3(2a2-3b2)=a2+b2-6a2-9b2
D. – (x - y) = y - xD 7.若2xmyn-2与 - 3y3x2是同类项,则m= ,
n= .

8.下列各式计算正确的是（ ）
A. 3a+2b=5ab B. 5x-3x=2

C. –t-t-t= - 3t D.6m2n-6mn2=0C25二、典型例题评析：
例1.化简计算：
(1)6y2 – 9y+5 - y2+4y - 5y2

(2)
(3)注意：①去括号时，考虑符号是否改变，不要漏 乘括号里的项；
②运用整体思想，可以简化运算过程.例2.求代数式的值:
1.当 ， 时,求x2+3xy-y2+1的值.2.当x=2,y=-1时,求
2(x2-y2)+0.5(4x+6y)-(2x+3y)-(x2-3)的值.3.已知 求 的值.4.已知x2+2y+5=7,求3x2-6y-3的值.直接代入化简代入整体代入【探索研究】
小明对小丽说：“你任想一个数，把这
个数乘以2，结果加上8，再除以2，最后减
去所想的数，我能马上知道结果”.请你解释
小明有什么诀窍？
例3. 在下列计算程序中填写适当的数 或转换 步骤.输入-2( )2-5输出注：给出程序，只需顺向计算, 先写的先算.
编写程序，必须逆向分析，先算的先写.
(1)输入 x输出( )2×3-5(2)输入输出11+2-5-1( )2
2或-6（3）按图所示的程序计算,若开始输入的数为x=3,则最后输出的结果是 ( )D【小试牛刀】【链接中考】 某市的出租车因车型不同，收费标准也
不同. A型车的起步价为10元，3km后每千
米加价1.2元；B型车的起步价为8元， 3km
后每千米加价1.4元.
（1）如果乘坐出租车到a（a>3)km的地方，
选择两种型号的车各需付多少钱？(2)如果乘坐出租车到20km的地方，从节省
费用的角度，请你选择出租车的型号.（3）乘坐出租车行驶多少千米，所付的钱数
一样多？例3.某汽车行驶时油箱中的余油量Q（升）与行 驶时间t（小时）的关系如下表： (1)写出用时间t表示余油量Q的代数式;
(2)求行驶2.5小时后油箱中的余油量;
(3)根据所列代数式回答,汽车行驶之前油箱中的余油量.（2）甲、乙两个仓库向A、B两地运送水泥，已知甲库可调100吨，已知乙库可调80吨，A地需70吨水泥，B地需110吨水泥，所用信息如下表（表中运费表示每吨水泥运送1千米所需人民币）问：要使总运费最省，该如何调运？例2.先化简，再求值.：一、基础知识回顾：
1.用代数式表示：
（1）a、b两数的平方差 ；
（2）m、n的倒数和 ；
（3）若n为整数，则三个连续偶数的和可以表示为 .a2-b26n ２.请你先设计出求代数式　　　的
值的程序，再填写下表：注：编写程序，必须逆向分析，
　　先算的先写.【探索研究】
化简求值:
(-m2+3mn-n2) – (m2-mn+n2)+2(m2-2mn),
其中,m= , n= - 1.小明把 m= 错抄
成m= ,但他的计算结果也是正确的,这是
为什么呢?
下列各式中,属于同类项的是 ( )
A. -4X与-4x2 B. 2 xy与-xz
C.5a2b与-3 ba3 D. -m2n、m2n与5nm2