第一章 反比例函数单元测试题(含答案)
文档属性
| 名称 | 第一章 反比例函数单元测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 19:51:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一章 反比例函数检测题(A)
一.选择题(共12小题,满分36分,每小题3分)
1.下列关系式中的y是x的反比例函数的个数( )
①,②,③y=1﹣x,④xy=1,⑤y=2x﹣1,⑥.
A.2个 B.3个 C.4个 D.5个
2.在同一平面直角坐标系中,函数y=与函数y=﹣x的图象交点个数是( )
A.0个 B.1个 C.2个 D.3个
3.已知函数y=(m+1)是反比例函数,且图象在第二、四象限内,则m值是( )
A.2 B.﹣2 C.±2 D.
4.反比例函数的图象在每个象限内,y随x的增大而增大,则a的取值范围是( )
A.a≥﹣3 B.a>﹣3 C.a≤﹣3 D.a<﹣3
5.已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
6.在同一平面直角坐标系中,函数y=kx﹣k与y=(k≠0)的图象大致是( )
A. B. C. D.
7.反比例函数的图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
8.点(﹣3,5)在反比例函数y=(k≠0)的图象上,则下列各点在该函数图象上的是( )
A.(5,﹣3) B.(﹣,3) C.(﹣5,﹣3) D.(,3)
9.若点(﹣3,y1),(﹣1,y2),(2,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y3<y1<y2 D.y1<y2<y3
10.如图,反比例函数的图象经过点A(2,1),若y≤1,则x的范围为( )
A.x≥1 B.x≥2 C.x<0或0<x≤1 D.x<0或x≥2
11.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数y=在第一象限内的图象经过点A,与BC交于点F,则△AOF面积等于( )
A.12 B.10 C.20 D.24
12.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差为( )
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分24分,每小题4分)
13.如图,直线y=kx(k≠0)与双曲线y=相交于A、C两点,过点A作AB⊥x轴于点B,连接BC,则△ABC的面积为 .
14.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2= .
15.如图,一次函数y1=ax+b(a≠0)与反比例函数y2=的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 .
16.如图,点A、D分别在函数y=的图象上,点B、C在x轴上,且OB=20C.若四边形ABCD为矩形,点D在第一象限,则k= .
17.如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .
18.如图,在平面直角坐标系中,正方形ABCD的顶点A与D在函数y=(x>0)的图象上,AC⊥x轴,垂足为C,点B的坐标为(0,2),则k的值为 .
三.解答题(共5小题,12+12+12+12+12,满分60分)
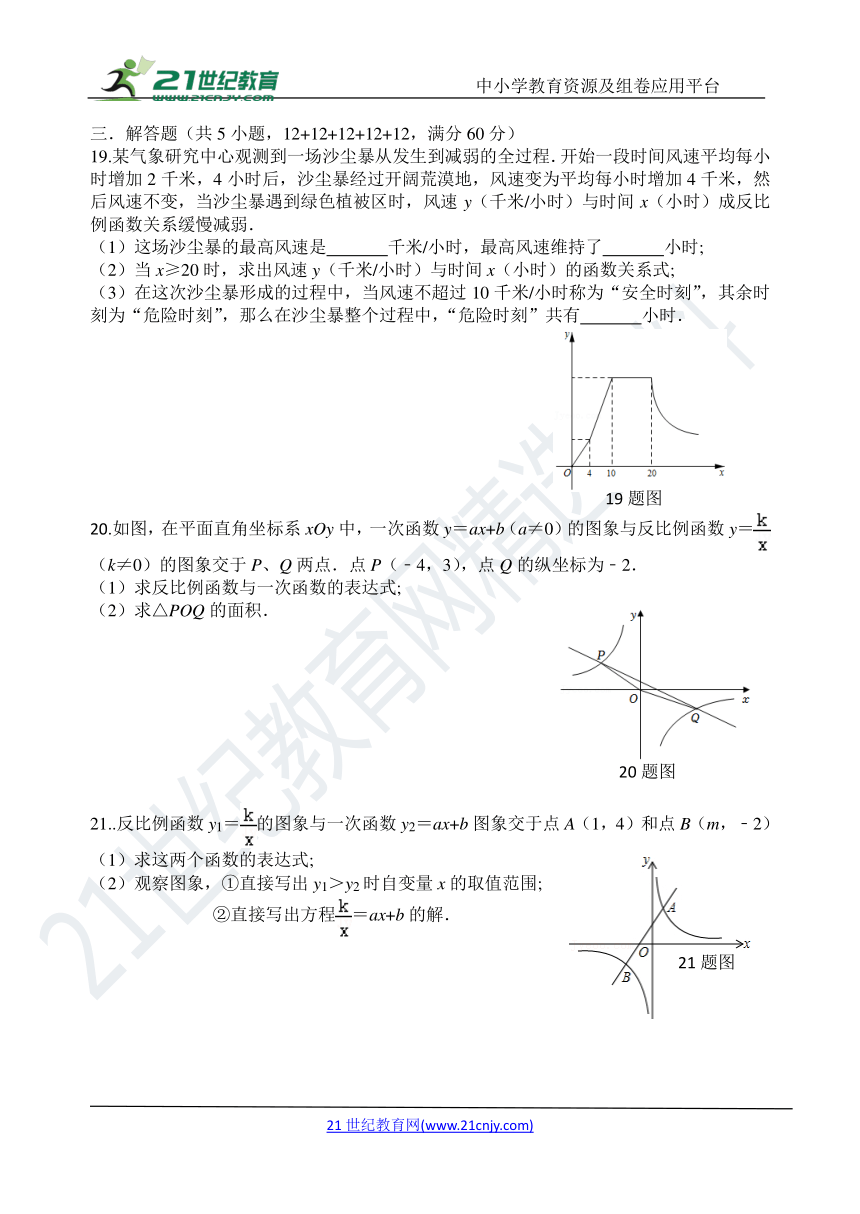
19.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时)与时间x(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是 千米/小时,最高风速维持了 小时;
(2)当x≥20时,求出风速y(千米/小时)与时间x(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,“危险时刻”共有 小时.
20.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于P、Q两点.点P(﹣4,3),点Q的纵坐标为﹣2.
(1)求反比例函数与一次函数的表达式;
(2)求△POQ的面积.
21..反比例函数y1=的图象与一次函数y2=ax+b图象交于点A(1,4)和点B(m,﹣2) (1)求这两个函数的表达式;
(2)观察图象,①直接写出y1>y2时自变量x的取值范围;
②直接写出方程=ax+b的解.
22.如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=图象上的一点,
△OPC与△ABC面积相等,请直接写出点P的坐标.
23.如图,在直角坐标系中,直线y=﹣x与反比例函数y=的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣x<的解集;
(3)将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为36,求平移后的直线的函数表达式.
第一章反比例函数单元达标测试卷A答案
一.选择题
1-5,CABDA; 6-10,BDACD; 11-12,BD.
二、填空题
13.S△ABC=4;14.S1+S2=6;15.x<0或1<x<4 ;16.k=﹣6;17.8; 18.8;
三.解答题(共7小题,满分66分)
19.解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时;10~20时,风速不变,最高风速维持时间为20﹣10=10小时;故答案为:32,10;
(2)设y=,
将(20,32)代入,得32=,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=;
(3)∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=,
得10=,解得x=64,
64﹣4.5=59.5(小时).
故在沙尘暴整个过程中,“危险时刻”共有 59.5小时. 故答案为:59.5.
20.解:(1)将点P(﹣4,3)代入反比例函数y=中,解得:k=﹣4×3=﹣12,
∴反比例函数的表达式为:y=﹣;
当y=﹣2时,﹣2=﹣,
∴x=6, ∴Q(6,﹣2),
将点P(﹣4,3)和Q(6,﹣2)代入y=ax+b中得:,
解得:,
∴一次函数的表达式为:y=﹣x+1;
(2)如图,
y=﹣x+1,
当x=0时,y=1,∴OM=1,
∴S△POQ=S△POM+S△OMQ=×1×4+×1×6=2+3=5.
21.解:(1)把点A(1,4)代入y1=,得到k=4,
∴y1=,把点B(m,﹣2)代入得到,m=﹣2,
把A(1,4)和点B(﹣2,﹣2)代入y2=ax+b得到,解得,
∴y2=2x+2.
(2)①由图象可知y1>y2成立时自变量x的取值范围:x<﹣2或0<x<1.
②方程=ax+b的解是x1=﹣2,x2=1.
22.解:(1)把x=2代入y=3x中,得y=2×3=6,
∴点A坐标为(2,6),
∵点A在反比例函数y=的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(﹣2,﹣6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2××2×6=12,
(3)∵S△ABC=12,
∴S△OPC=12,
设P点坐标为(x,),则P到OC的距离为||,
∴×||×2=12,解得x=1或﹣1,
∴P点坐标为(1,12)或(﹣1,﹣12).
23.解:(1)令一次函数y=﹣x中y=3,则3=﹣x,
解得:x=﹣6,即点A的坐标为(﹣6,3),
∵点A(﹣6,3)在反比例函数y=的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣;
(2)由图象可知,﹣x<的解集为﹣6<x<0或x>6;
(3)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为36,
∴S△ABF=OF (xB﹣xA)=36,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴b×12=36,
∴b=6,
∴平移后的直线的函数表达式为y=﹣x+6.
10题图
11题图
12题图
13题图
14题图
15题图
16题图
17题图
18题图
19题图
20题图
21题图
22题图
23题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第一章 反比例函数检测题(A)
一.选择题(共12小题,满分36分,每小题3分)
1.下列关系式中的y是x的反比例函数的个数( )
①,②,③y=1﹣x,④xy=1,⑤y=2x﹣1,⑥.
A.2个 B.3个 C.4个 D.5个
2.在同一平面直角坐标系中,函数y=与函数y=﹣x的图象交点个数是( )
A.0个 B.1个 C.2个 D.3个
3.已知函数y=(m+1)是反比例函数,且图象在第二、四象限内,则m值是( )
A.2 B.﹣2 C.±2 D.
4.反比例函数的图象在每个象限内,y随x的增大而增大,则a的取值范围是( )
A.a≥﹣3 B.a>﹣3 C.a≤﹣3 D.a<﹣3
5.已知经过闭合电路的电流I(单位:A)与电路的电阻R(单位:Ω)是反比例函数关系.根据下表判断a和b的大小关系为( )
I/A 5 … a … … … b … 1
R/Ω 20 30 40 50 60 70 80 90 100
A.a>b B.a≥b C.a<b D.a≤b
6.在同一平面直角坐标系中,函数y=kx﹣k与y=(k≠0)的图象大致是( )
A. B. C. D.
7.反比例函数的图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
8.点(﹣3,5)在反比例函数y=(k≠0)的图象上,则下列各点在该函数图象上的是( )
A.(5,﹣3) B.(﹣,3) C.(﹣5,﹣3) D.(,3)
9.若点(﹣3,y1),(﹣1,y2),(2,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是( )
A.y2<y1<y3 B.y3<y2<y1 C.y3<y1<y2 D.y1<y2<y3
10.如图,反比例函数的图象经过点A(2,1),若y≤1,则x的范围为( )
A.x≥1 B.x≥2 C.x<0或0<x≤1 D.x<0或x≥2
11.如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=,反比例函数y=在第一象限内的图象经过点A,与BC交于点F,则△AOF面积等于( )
A.12 B.10 C.20 D.24
12.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差为( )
A.1 B.2 C.3 D.4
二.填空题(共6小题,满分24分,每小题4分)
13.如图,直线y=kx(k≠0)与双曲线y=相交于A、C两点,过点A作AB⊥x轴于点B,连接BC,则△ABC的面积为 .
14.如图,A、B两点在双曲线y=上,分别经过A、B两点向坐标轴作垂线段,已知S阴影=1,则S1+S2= .
15.如图,一次函数y1=ax+b(a≠0)与反比例函数y2=的图象交于A(1,4)、B(4,1)两点,若使y1>y2,则x的取值范围是 .
16.如图,点A、D分别在函数y=的图象上,点B、C在x轴上,且OB=20C.若四边形ABCD为矩形,点D在第一象限,则k= .
17.如图,点A,C分别是正比例函数y=x的图象与反比例函数y=的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为 .
18.如图,在平面直角坐标系中,正方形ABCD的顶点A与D在函数y=(x>0)的图象上,AC⊥x轴,垂足为C,点B的坐标为(0,2),则k的值为 .
三.解答题(共5小题,12+12+12+12+12,满分60分)
19.某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时)与时间x(小时)成反比例函数关系缓慢减弱.
(1)这场沙尘暴的最高风速是 千米/小时,最高风速维持了 小时;
(2)当x≥20时,求出风速y(千米/小时)与时间x(小时)的函数关系式;
(3)在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,“危险时刻”共有 小时.
20.如图,在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=(k≠0)的图象交于P、Q两点.点P(﹣4,3),点Q的纵坐标为﹣2.
(1)求反比例函数与一次函数的表达式;
(2)求△POQ的面积.
21..反比例函数y1=的图象与一次函数y2=ax+b图象交于点A(1,4)和点B(m,﹣2) (1)求这两个函数的表达式;
(2)观察图象,①直接写出y1>y2时自变量x的取值范围;
②直接写出方程=ax+b的解.
22.如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=图象上的一点,
△OPC与△ABC面积相等,请直接写出点P的坐标.
23.如图,在直角坐标系中,直线y=﹣x与反比例函数y=的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣x<的解集;
(3)将直线y=﹣x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为36,求平移后的直线的函数表达式.
第一章反比例函数单元达标测试卷A答案
一.选择题
1-5,CABDA; 6-10,BDACD; 11-12,BD.
二、填空题
13.S△ABC=4;14.S1+S2=6;15.x<0或1<x<4 ;16.k=﹣6;17.8; 18.8;
三.解答题(共7小题,满分66分)
19.解:(1)0~4时,风速平均每小时增加2千米,所以4时风速为8千米/时;
4~10时,风速变为平均每小时增加4千米,10时达到最高风速,为8+6×4=32千米/时;10~20时,风速不变,最高风速维持时间为20﹣10=10小时;故答案为:32,10;
(2)设y=,
将(20,32)代入,得32=,
解得k=640.
所以当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系为y=;
(3)∵4时风速为8千米/时,而4小时后,风速变为平均每小时增加4千米,
∴4.5时风速为10千米/时,
将y=10代入y=,
得10=,解得x=64,
64﹣4.5=59.5(小时).
故在沙尘暴整个过程中,“危险时刻”共有 59.5小时. 故答案为:59.5.
20.解:(1)将点P(﹣4,3)代入反比例函数y=中,解得:k=﹣4×3=﹣12,
∴反比例函数的表达式为:y=﹣;
当y=﹣2时,﹣2=﹣,
∴x=6, ∴Q(6,﹣2),
将点P(﹣4,3)和Q(6,﹣2)代入y=ax+b中得:,
解得:,
∴一次函数的表达式为:y=﹣x+1;
(2)如图,
y=﹣x+1,
当x=0时,y=1,∴OM=1,
∴S△POQ=S△POM+S△OMQ=×1×4+×1×6=2+3=5.
21.解:(1)把点A(1,4)代入y1=,得到k=4,
∴y1=,把点B(m,﹣2)代入得到,m=﹣2,
把A(1,4)和点B(﹣2,﹣2)代入y2=ax+b得到,解得,
∴y2=2x+2.
(2)①由图象可知y1>y2成立时自变量x的取值范围:x<﹣2或0<x<1.
②方程=ax+b的解是x1=﹣2,x2=1.
22.解:(1)把x=2代入y=3x中,得y=2×3=6,
∴点A坐标为(2,6),
∵点A在反比例函数y=的图象上,
∴k=2×6=12,
∴反比例函数的解析式为y=;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(﹣2,﹣6),
∴B到OC的距离为6,
∴S△ABC=2S△ACO=2××2×6=12,
(3)∵S△ABC=12,
∴S△OPC=12,
设P点坐标为(x,),则P到OC的距离为||,
∴×||×2=12,解得x=1或﹣1,
∴P点坐标为(1,12)或(﹣1,﹣12).
23.解:(1)令一次函数y=﹣x中y=3,则3=﹣x,
解得:x=﹣6,即点A的坐标为(﹣6,3),
∵点A(﹣6,3)在反比例函数y=的图象上,
∴k=﹣6×3=﹣18,
∴反比例函数的表达式为y=﹣;
(2)由图象可知,﹣x<的解集为﹣6<x<0或x>6;
(3)设平移后直线于y轴交于点F,连接AF、BF如图所示.
设平移后的解析式为y=﹣x+b,
∵该直线平行直线AB,
∴S△ABC=S△ABF,
∵△ABC的面积为36,
∴S△ABF=OF (xB﹣xA)=36,
由对称性可知:xB=﹣xA,
∵xA=﹣6,
∴xB=6,
∴b×12=36,
∴b=6,
∴平移后的直线的函数表达式为y=﹣x+6.
10题图
11题图
12题图
13题图
14题图
15题图
16题图
17题图
18题图
19题图
20题图
21题图
22题图
23题图
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
