垂径定理1

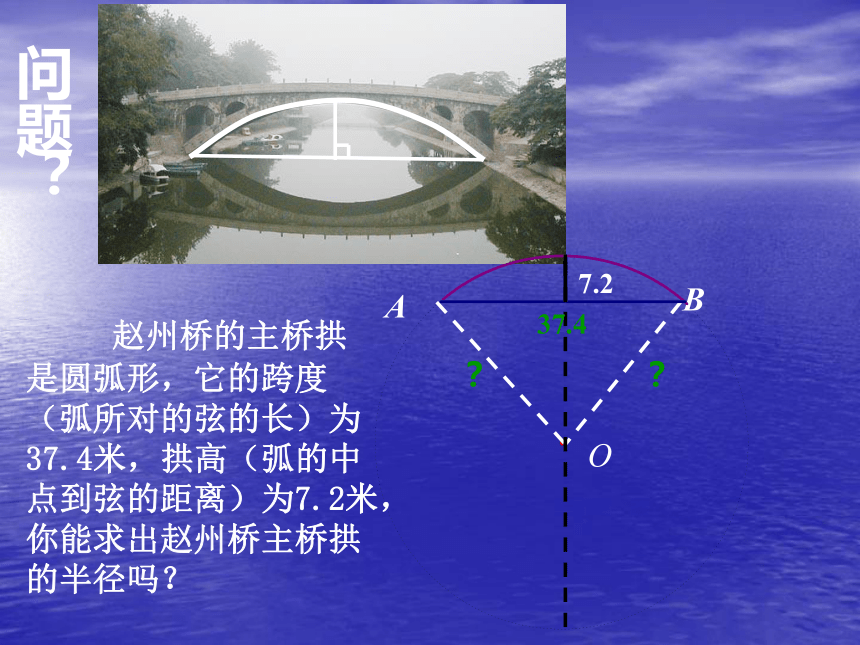
课件20张PPT。垂径定理1 赵州桥的主桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离）为7.2米，你能求出赵州桥主桥拱的半径吗？问题？OAB7.237.4？？如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
（1）圆是轴对称图形吗？如果是，它的对称轴是什么？
（2）你能发现图中有那些相等的线段和弧？为什么？·OABCDE活 动 一 （1）是轴对称图形．直径CD所在的直线是它的对称轴（2） 线段： AE=BE弧：把圆沿着直径CD折叠时，CD两侧的两个半圆重合，
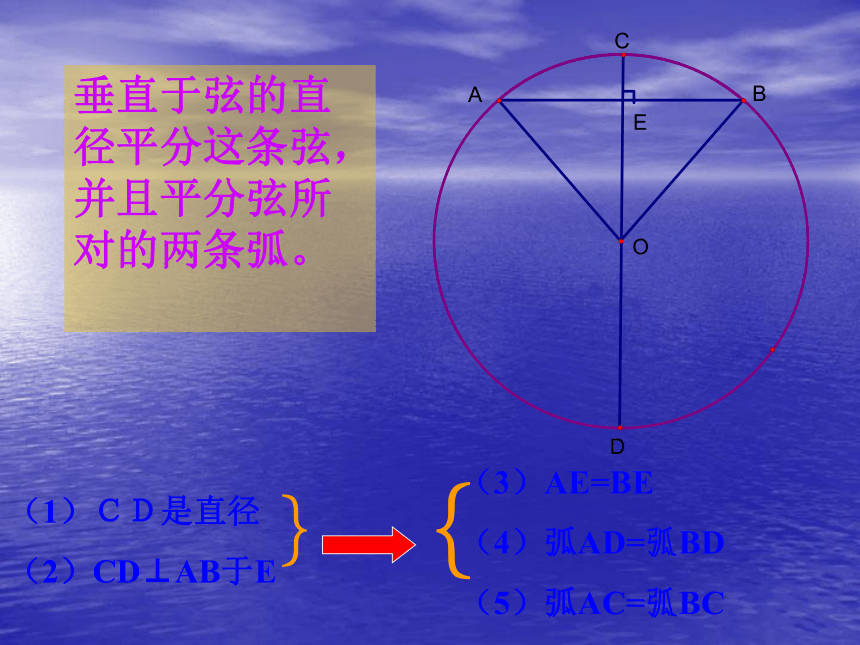
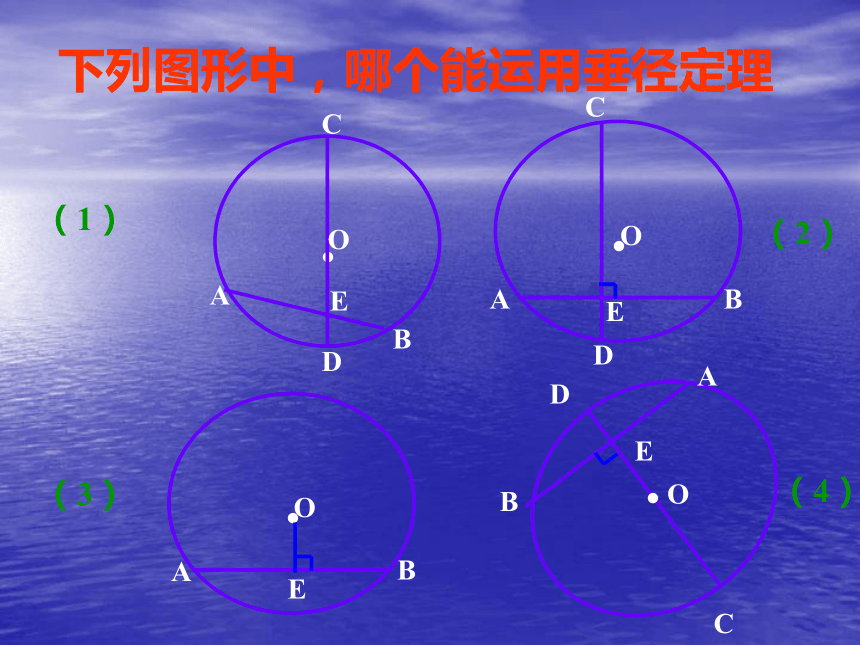
点A与点B重合，AE与BE重合， ， 分别与 、 重合．垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。下列图形中，哪个能运用垂径定理C图形分析：
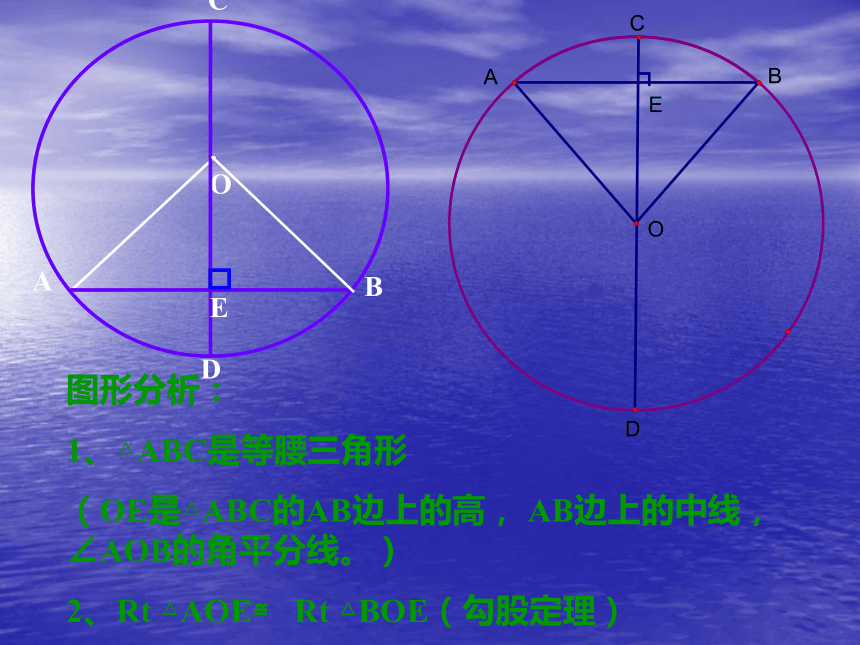
1、△ABC是等腰三角形
（OE是△ABC的AB边上的高， AB边上的中线，∠AOB的角平分线。）
2、Rt △AOE≌ Rt △BOE（勾股定理）BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．若AB=8，AO=5则，OE= ，DE= 。 思路指导：求圆中有关线段的长度时,常借助垂径定理转化为直角三角形,从而利用勾股定理来解决问题. 一、已半径知弦长，求弦心距和弓高BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
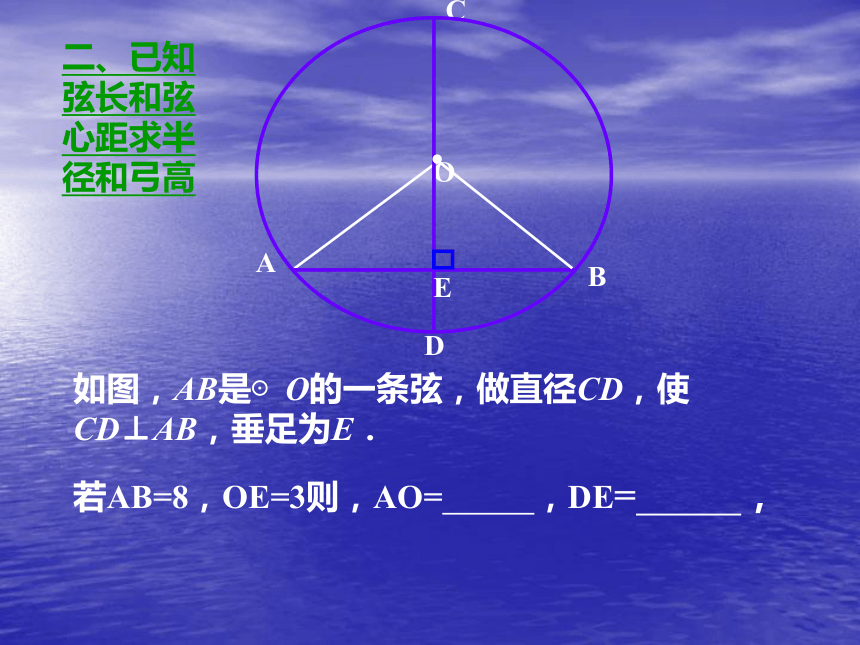
若AB=8，OE=3则，AO= ，DE= ，
二、已知弦长和弦心距求半径和弓高BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
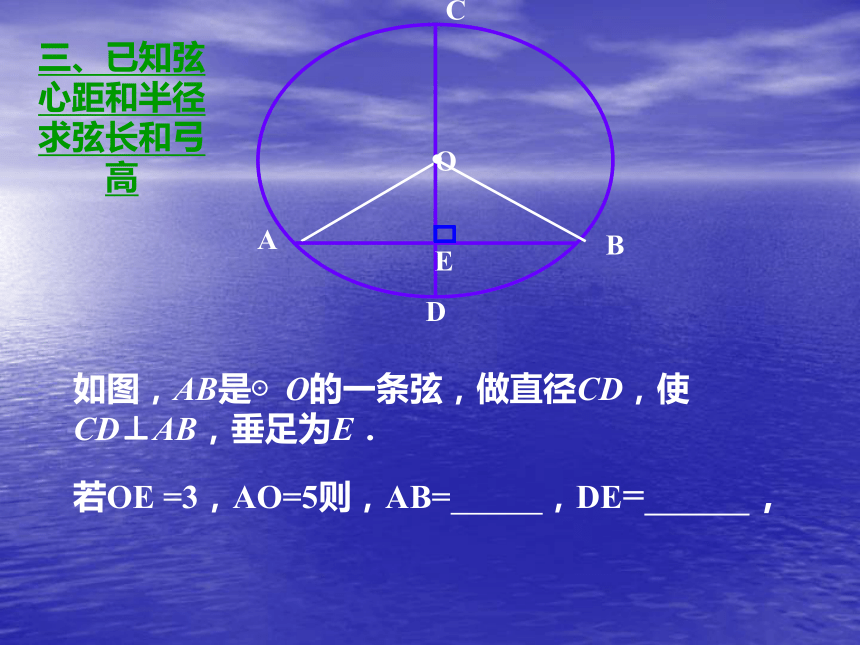
若OE =3，AO=5则，AB= ，DE= ，
三、已知弦心距和半径求弦长和弓高BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
若DE =2，AO=5则，OE= ，AB= ，
四、已知弓高和半径求弦长和弦心距 BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
若OE =3， DE =2则，AO= ， AB= ，五、已知弦心距和弓高求半径和弦长BC.如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
若AB=8，DE=2则，OE= ，AO= ，
六、已知弦长和弓高求弦心距和半径小结：在圆的半径，弦长，弦心距及弓高四个量中，只要已知两个量，我们就可以借助勾股定理求出另外的两个量。*特别知道弓高和弦长借助于列方程。赵州石拱桥解：如图，用 表示桥拱， 所在圆的圆心为O，半径为Rm，
经过圆心O作弦AB的垂线OD，D为垂足，与 相交于点C.根
据垂径定理，D是AB的中点，C是 的中点，CD就是拱高.
由题设在Rt△OAD中，由勾股定理，得解得 R≈27.9（m）.答：赵州石拱桥的桥拱半径约为27.9m.解决有关弦的问题时，经常连结半径；过圆心作一条与弦垂直的线段等辅助线，为应用垂径定理创造条件。方法归纳：变式2：如图：OA=OB，
AC=BD吗？为什么？
ACDBO图３练一练练一练练一练1、 在⊙ O中，若弦AB的长为8cm，圆心到弦的距离为3cm，则⊙ O的半径为（ ）cm。
2、已知：如图，在⊙ O中，AB、
AC为互相垂直的两条相等的弦，
OD ⊥AB，OE ⊥AC，D、E为垂足.
求四边形ADOE的形状.已知⊙O的半径为10，弦AB∥CD，AB=12，CD=16，则AB和CD的距离为 ． 2或14提高练习:212.O.O
谢 谢 各 位作 业P68：7、12