鲁教版九年级下学期期末测试数学试题A(含答案)
文档属性
| 名称 | 鲁教版九年级下学期期末测试数学试题A(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 951.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 18:53:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
九年级数学期末测试题(B)
第Ⅰ卷(选择题 共36分)
选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求。)
1.如图的几何体是由五个相同的小立方体搭成,它的左视图是( )
A. B. C. D.
2. 下列函数中,对于任意实数,,当时,满足的是( )
A.y=-3x+2 B.y=2x+1 C. D.
3.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为( )cm.
A. B. C. D.
4.抛物线y=x+bx+c的图象先向下平移3个单位,再向右平移2个单位,所得图
的函数表达式为,则b,c的值为( )
A. b=2,c=-6 B. b=2,c=0 C. b=-6,c=8 D. b=-6,c=2
5.如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,连接D D′,则tan∠DD′C= ( )
A. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
6.如图,AB与⊙O相切与点B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧BC的弧长为( )
A. B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
7.有五张正面分别写有数字-3,-2,1,2,3的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,然后再从剩余的四张卡片中随机抽取一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率是( )
A. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
8.九年级数学期末测试题(B)在同一平面直角坐标系中,函数 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 和函数 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT (m是常数,且m≠0)的图象可能是( )
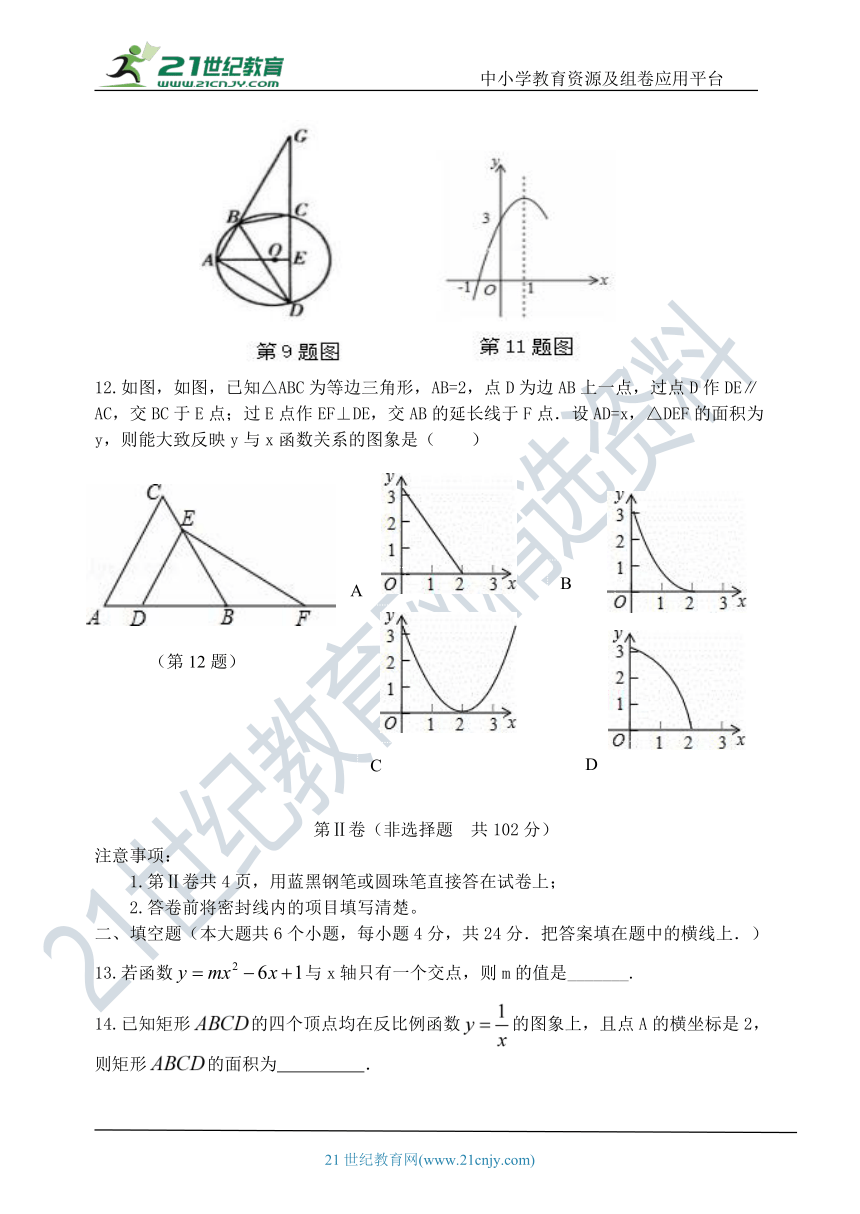
9.如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( ).
A.50° B.60° C.80° D.85°
10.一次函数的图像经过点A(),B(2,2)两点,P为反比例函数图像上的一个动点,O为坐标原点,过P作y轴的垂线,垂足为C, 则△PCO的面积为( )
A.2 B.4 C.8 D.不确定
11.如图,抛物线(a≠0)的对称轴为直=1,与轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程=0的两个根是,; ③;④当时,的取值范围是;⑤当时,.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
12.如图,如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
第Ⅱ卷(非选择题 共102分)
注意事项:
1.第Ⅱ卷共4页,用蓝黑钢笔或圆珠笔直接答在试卷上;
2.答卷前将密封线内的项目填写清楚。
填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)
13.若函数与x轴只有一个交点,则m的值是_______.
14.已知矩形 ( http: / / www." \o "中国教育出版网\ )的四个顶点均在反比例函数 ( http: / / www." \o "中国教育出版网\ )的图象上,且点A的横坐标是2,则矩形 ( http: / / www." \o "中国教育出版网\ )的面积为 .
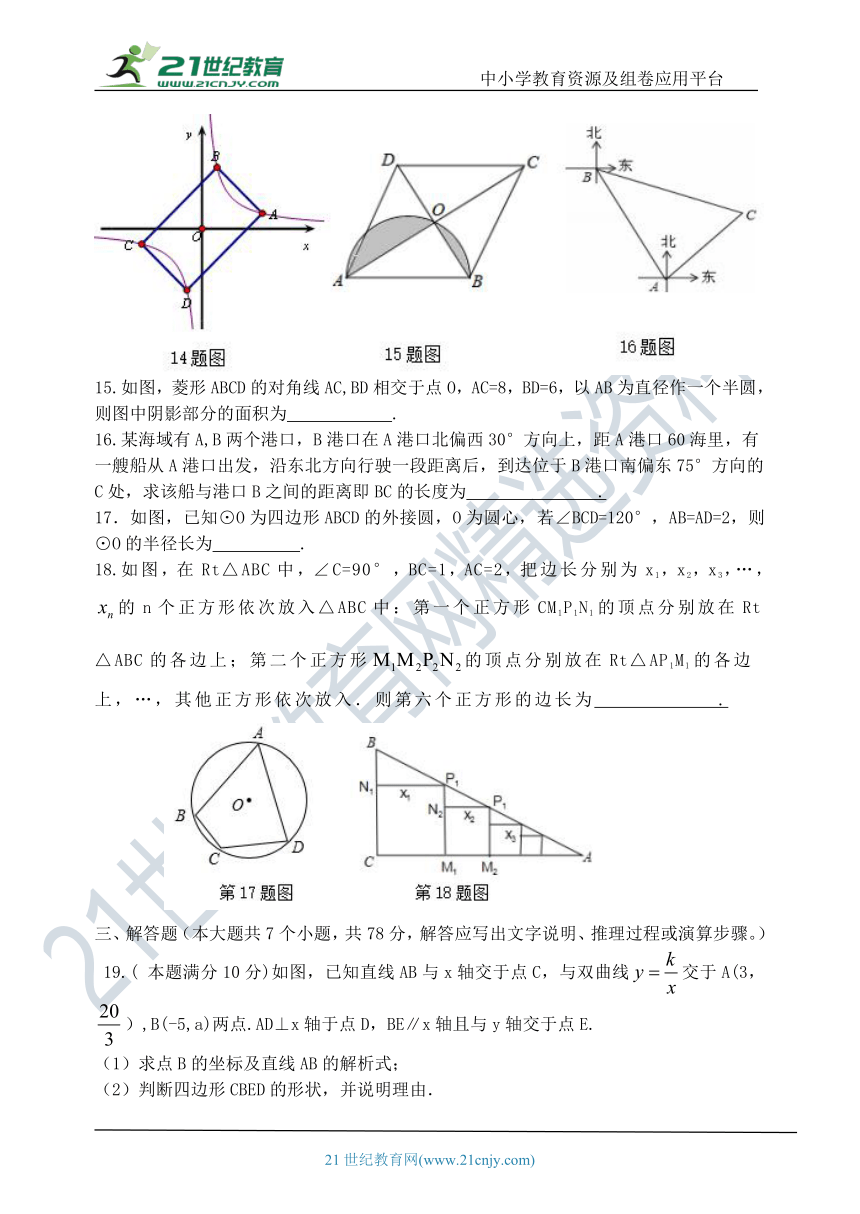
15.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为 .
16.某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为 .
17.如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为 .
18.如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,的n个正方形依次放入△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入.则第六个正方形的边长为 .
三、解答题(本大题共7个小题,共78分,解答应写出文字说明、推理过程或演算步骤。)
19.( 本题满分10分)如图,已知直线AB与x轴交于点C,与双曲线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 交于A(3, QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ),B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
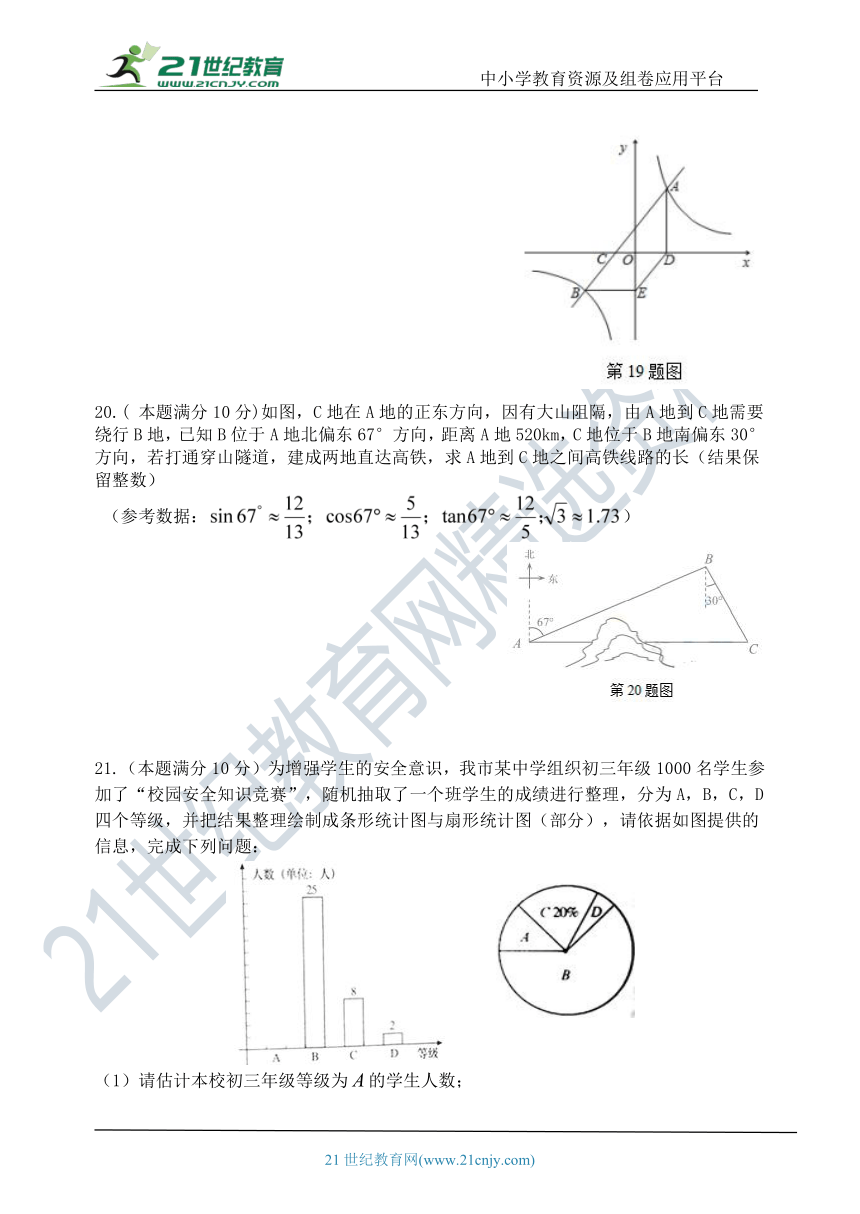
20.( 本题满分10分)如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:)
21.(本题满分10分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取了一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取2人参加市级比赛,请求出恰好抽到1名女生和1名男生的概率.
22.(本题满分10分)已知:如图,MN为⊙O的直径,ME⊙O是的弦,MD ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )垂直于过点的直线DE ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ),垂足为点D ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ),且ME ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )平分∠DMN ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ).求证:(1)DE ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )是⊙O ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )的切线;(2)ME=MDMN
23.(本题满分12分)
如图,在正方形ABCD中,点O是对角线AC,BD的交点,点E在CD上,连接BE,过点C作CF⊥BE于点F,在BE上截取BG=CF,连接OF,OG.
(1)求证:△BOG≌△COF; (2) 若AB=6,DE=2CE,求OF的长度.
24.(本题满分12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
⑴ 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
⑵每件衬衫降价多少元,商场平均每天盈利最多?
25.(本题满分14分)如图,直线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 与抛物线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 相交于点A( QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ,)和(4,m)两点,点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的点P,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)直接写出当△PAC为直角三角形时点P的坐标.
九年级数学期末测试B参考答案
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可;
2.若考生的解法与给出的解法不同,正确者相应给分;
一、选择题(本大题共12个小题,每小题4分,共48分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B B B B C D C A
题号 11 12
答案 C B
二、填空题(本大题共6个小题,每小题4分,共24分。)
13.m=9或m=0 14. 15.π-6 16. +10)海里 17. 18. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ;
三、解答题
19.解:(1)∵双曲线过A(3,20/3),
∴k=20.把B(-5,a)代入y=20/x, 得a=-4.
∴点B的坐标是(-5,-4).
设直线AB的解析式为y=mx+n, 将 A(3,20/3),B(-5,-4)代入,
解得:m=4/3. n=8/3
∴直线AB的解析式为:.y=4/3x+8/3 ……………………………………4分
(2)四边形CBED是菱形.
理由如下: 点D的坐标是(3,0),点C的坐标是(-2,0).
∵ BE∥轴, ∴点E的坐标是(0,-4).
∴ CD =5, BE=5, 且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,
∴ ED=5,∴ED=CD.
∴四边形CBED是菱形……………………………………………10分
20(10分)
(2)
22.(10分)
23.(12分)
(1)证明在正方形ABCD中
∵RT△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中
OB=OC ∠OBG=∠OCF BG=CF
∴△OBG≌△OCF(SAS)..........................5分
(2)∵△OBG≌△OCF
∴OG=OF,∠BOG=∠COF,BG=CF
∵∠BOC=90°∴∠GOF=90°∴∠OFG=∴∠OGF=45°
在Rt△BCE中,BC=DC=6,DE=2EC,
∴EC=2,
∴BE= = = ,
∵CF=
∴BF= ,BG=CF=
∴GF=BF-BG=
在等腰直角△OGF中
OF………………10分
24解:(1)设每件衬衫应降价x元,
则依题意,得:
整理,得:
解得:
因为要“扩大销售量,减少库存”应选择降价20元
∴若商场平均每天赢利1200元,每件衬衫应降价20元;
(2)设每件衬衫降价x元时,商场平均每天赢利最多为y,
则
∴x=15时,赢利最多,此时y=1250元
∴每件衬衫降价15元时,商场平均每天赢利最多。
25.(14分)解:(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6, ∴B(4,6),
∵A(),B(4,6)在抛物线y=a+bx+6上,
∴,解得,
∴抛物线的解析式为y=2﹣8x+6.……………………5分
(2)设动点P的坐标为(t,t+2),则C点的坐标为(t,2﹣8t+6),
∴PC=(t+2)﹣(2﹣8t+6) =-2+9t-4 =﹣2-+=
∴当t=时,线段PC最大且为.……………10分
(3)点P的坐标为(3,5)或)…………14分
第5题图
第6题图
A
B
C
D
(第12题)
(第22题图)
(第23题)
A
D
E
B
C
G
F
O
(第25题)
(第19题)
(第23题)
A
D
E
B
C
G
F
O
(第25题)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学期末测试题(B)
第Ⅰ卷(选择题 共36分)
选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求。)
1.如图的几何体是由五个相同的小立方体搭成,它的左视图是( )
A. B. C. D.
2. 下列函数中,对于任意实数,,当时,满足的是( )
A.y=-3x+2 B.y=2x+1 C. D.
3.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为( )cm.
A. B. C. D.
4.抛物线y=x+bx+c的图象先向下平移3个单位,再向右平移2个单位,所得图
的函数表达式为,则b,c的值为( )
A. b=2,c=-6 B. b=2,c=0 C. b=-6,c=8 D. b=-6,c=2
5.如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD′,连接D D′,则tan∠DD′C= ( )
A. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
6.如图,AB与⊙O相切与点B,OA=2,∠OAB=30°,弦BC∥OA,则劣弧BC的弧长为( )
A. B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
7.有五张正面分别写有数字-3,-2,1,2,3的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,然后再从剩余的四张卡片中随机抽取一张,以其正面的数字作为b的值,则点(a,b)在第二象限的概率是( )
A. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT B. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT C. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT D. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT
8.九年级数学期末测试题(B)在同一平面直角坐标系中,函数 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 和函数 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT (m是常数,且m≠0)的图象可能是( )
9.如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( ).
A.50° B.60° C.80° D.85°
10.一次函数的图像经过点A(),B(2,2)两点,P为反比例函数图像上的一个动点,O为坐标原点,过P作y轴的垂线,垂足为C, 则△PCO的面积为( )
A.2 B.4 C.8 D.不确定
11.如图,抛物线(a≠0)的对称轴为直=1,与轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ;②方程=0的两个根是,; ③;④当时,的取值范围是;⑤当时,.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
12.如图,如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
第Ⅱ卷(非选择题 共102分)
注意事项:
1.第Ⅱ卷共4页,用蓝黑钢笔或圆珠笔直接答在试卷上;
2.答卷前将密封线内的项目填写清楚。
填空题(本大题共6个小题,每小题4分,共24分.把答案填在题中的横线上.)
13.若函数与x轴只有一个交点,则m的值是_______.
14.已知矩形 ( http: / / www." \o "中国教育出版网\ )的四个顶点均在反比例函数 ( http: / / www." \o "中国教育出版网\ )的图象上,且点A的横坐标是2,则矩形 ( http: / / www." \o "中国教育出版网\ )的面积为 .
15.如图,菱形ABCD的对角线AC,BD相交于点O,AC=8,BD=6,以AB为直径作一个半圆,则图中阴影部分的面积为 .
16.某海域有A,B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求该船与港口B之间的距离即BC的长度为 .
17.如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为 .
18.如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,的n个正方形依次放入△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形的顶点分别放在Rt△AP1M1的各边上,…,其他正方形依次放入.则第六个正方形的边长为 .
三、解答题(本大题共7个小题,共78分,解答应写出文字说明、推理过程或演算步骤。)
19.( 本题满分10分)如图,已知直线AB与x轴交于点C,与双曲线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 交于A(3, QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ),B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.
20.( 本题满分10分)如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:)
21.(本题满分10分)为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取了一个班学生的成绩进行整理,分为A,B,C,D四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
(1)请估计本校初三年级等级为的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取2人参加市级比赛,请求出恰好抽到1名女生和1名男生的概率.
22.(本题满分10分)已知:如图,MN为⊙O的直径,ME⊙O是的弦,MD ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )垂直于过点的直线DE ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ),垂足为点D ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ),且ME ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )平分∠DMN ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" ).求证:(1)DE ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )是⊙O ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" )的切线;(2)ME=MDMN
23.(本题满分12分)
如图,在正方形ABCD中,点O是对角线AC,BD的交点,点E在CD上,连接BE,过点C作CF⊥BE于点F,在BE上截取BG=CF,连接OF,OG.
(1)求证:△BOG≌△COF; (2) 若AB=6,DE=2CE,求OF的长度.
24.(本题满分12分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
⑴ 若商场平均每天要盈利1200元,每件衬衫应降价多少元?
⑵每件衬衫降价多少元,商场平均每天盈利最多?
25.(本题满分14分)如图,直线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 与抛物线 QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT 相交于点A( QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ,)和(4,m)两点,点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的点P,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)直接写出当△PAC为直角三角形时点P的坐标.
九年级数学期末测试B参考答案
阅卷须知:
1.为便于阅卷,本试卷答案中有关解答题的推导步骤写得较为详细,阅卷时,只要考生将主要过程正确写出即可;
2.若考生的解法与给出的解法不同,正确者相应给分;
一、选择题(本大题共12个小题,每小题4分,共48分.)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B B B B C D C A
题号 11 12
答案 C B
二、填空题(本大题共6个小题,每小题4分,共24分。)
13.m=9或m=0 14. 15.π-6 16. +10)海里 17. 18. QUOTE EMBED Equation.KSEE3 \* MERGEFORMAT ;
三、解答题
19.解:(1)∵双曲线过A(3,20/3),
∴k=20.把B(-5,a)代入y=20/x, 得a=-4.
∴点B的坐标是(-5,-4).
设直线AB的解析式为y=mx+n, 将 A(3,20/3),B(-5,-4)代入,
解得:m=4/3. n=8/3
∴直线AB的解析式为:.y=4/3x+8/3 ……………………………………4分
(2)四边形CBED是菱形.
理由如下: 点D的坐标是(3,0),点C的坐标是(-2,0).
∵ BE∥轴, ∴点E的坐标是(0,-4).
∴ CD =5, BE=5, 且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,
∴ ED=5,∴ED=CD.
∴四边形CBED是菱形……………………………………………10分
20(10分)
(2)
22.(10分)
23.(12分)
(1)证明在正方形ABCD中
∵RT△BCE中,CF⊥BE,
∴∠EBC=∠ECF,
∵∠OBC=∠OCD=45°,
∴∠OBG=∠OCF,
在△OBG与△OCF中
OB=OC ∠OBG=∠OCF BG=CF
∴△OBG≌△OCF(SAS)..........................5分
(2)∵△OBG≌△OCF
∴OG=OF,∠BOG=∠COF,BG=CF
∵∠BOC=90°∴∠GOF=90°∴∠OFG=∴∠OGF=45°
在Rt△BCE中,BC=DC=6,DE=2EC,
∴EC=2,
∴BE= = = ,
∵CF=
∴BF= ,BG=CF=
∴GF=BF-BG=
在等腰直角△OGF中
OF………………10分
24解:(1)设每件衬衫应降价x元,
则依题意,得:
整理,得:
解得:
因为要“扩大销售量,减少库存”应选择降价20元
∴若商场平均每天赢利1200元,每件衬衫应降价20元;
(2)设每件衬衫降价x元时,商场平均每天赢利最多为y,
则
∴x=15时,赢利最多,此时y=1250元
∴每件衬衫降价15元时,商场平均每天赢利最多。
25.(14分)解:(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6, ∴B(4,6),
∵A(),B(4,6)在抛物线y=a+bx+6上,
∴,解得,
∴抛物线的解析式为y=2﹣8x+6.……………………5分
(2)设动点P的坐标为(t,t+2),则C点的坐标为(t,2﹣8t+6),
∴PC=(t+2)﹣(2﹣8t+6) =-2+9t-4 =﹣2-+=
∴当t=时,线段PC最大且为.……………10分
(3)点P的坐标为(3,5)或)…………14分
第5题图
第6题图
A
B
C
D
(第12题)
(第22题图)
(第23题)
A
D
E
B
C
G
F
O
(第25题)
(第19题)
(第23题)
A
D
E
B
C
G
F
O
(第25题)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
