八年级数学下册-北师大版 1.1.1等腰三角形导学案
文档属性
| 名称 | 八年级数学下册-北师大版 1.1.1等腰三角形导学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 10:39:42 | ||
图片预览


文档简介
1.1.1 等腰三角形
导学案
学习目标
1、探索证明等腰三角形性质定理的思路与方法。
2、掌握证明的基本要求和方法。
学习重点:探索证明等腰三角形性质定理的思路与方法。
学习难点:掌握证明的基本要求和方法。
一、自学释疑
探索证明等腰三角形性质定理的过程中,应该注意些什么?
二、思学质疑
把你在本次课程学习中的困惑与建议填写在下面,与同学交流后,由组长整理后并拍照上传平台讨论区。
__________________________________________________________________________________________________________________________________________
三、合作探究
问题1:根据学过的基本事实和已知的定理,能证明“两角分别相等且其中一组等角的对边相等的两个三角形全等”吗?与同伴交流,展示你的说理过程。
如:已知:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
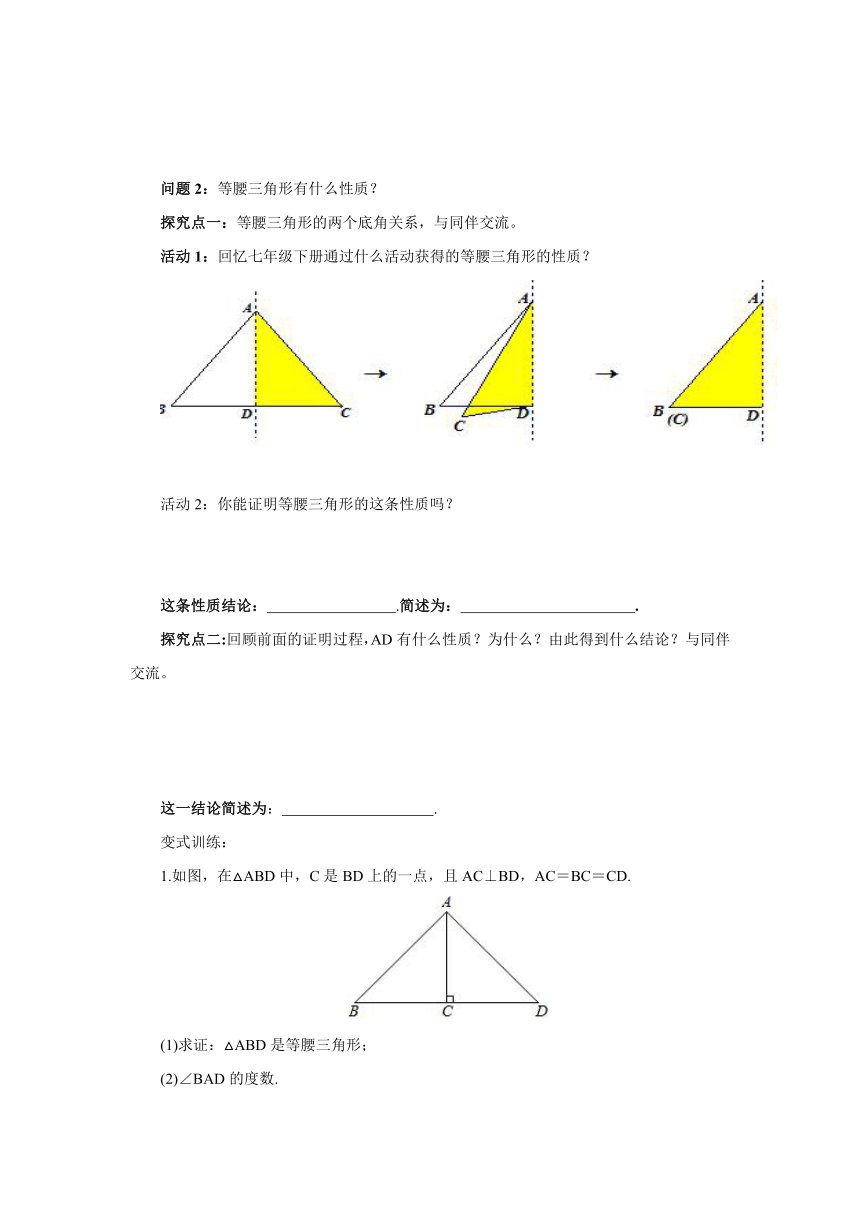
问题2:等腰三角形有什么性质?
探究点一:等腰三角形的两个底角关系,与同伴交流。
活动1:回忆七年级下册通过什么活动获得的等腰三角形的性质?
活动2:你能证明等腰三角形的这条性质吗?
这条性质结论: .简述为: .
探究点二:回顾前面的证明过程,AD有什么性质?为什么?由此得到什么结论?与同伴交流。
这一结论简述为: .
变式训练:
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)∠BAD的度数.
四、随堂检测
1.等腰三角形的一个角是80°,则它顶角的度数是( )
A.80° B.80°或20° C.80°或50° D.20°
2.已知等腰三角形的两边长分别是3和5,则该三角形的周长是( )
A.8 B.9 C.10或12 D.11或13
3.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A.7 B.11 C.7或11 D.7或10
4.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或150° D.60°或120°
5.在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18 ° D.64°
6.△ABC中,AB=BD=DC,∠C=40°,则∠A=________,∠ABD=_______.
7.△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
①求证:△ABD是等腰三角形
② 求∠BAD的度数.
我的收获
1、 .
2、教会学生根据已知条件选择合适的证明方法解题.
参考答案
问题1:证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°。
∴ ∠C=180°-(∠A+∠B),
∠F=180°-(∠D+∠E) 。
∵∠A=∠D,∠B=∠E ∴∠C=∠F。
∵ BC=EF,∴△ABC≌△DEF
问题2:
探究点一:活动2:证明:如图,取BC的中点为D,连接AD
∵AB=AC,BD=CD,AD=AD,
∴△ABD△≌△ACD(SSS).
∴∠B=∠C (全等三角形的对应角相等).
等腰三角形的两底角相等.等边对等角·
探究点二:
解:AD是底边上的中线,也是底边上的高,同时也是顶角的平分线;
理由如下:过顶点A作∠BAC的平分线AD,交BC于点D,
∵AD是△ABC中的角平分线,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形的对应边相等),
∠ADB=∠ADC(全等三角形的对应角相等).
∴AD是BC边上的中线,
∠BDA=90°,
∴AD是BC边上的高,
∴等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。
三线合一.
变式训练:
1.证明:(1)∵AC⊥BD(已知)
∴∠ACB=∠ACD=90°(垂直定义)
△ABC与△ADC中
AC=AC
∠ACB=∠ACD
BC=DC
∴△ABC≌△ADC(SAS)
AB=AD(全等三角形对应边相等)
∴△ABD是等腰三角形(等腰三角形的定义)
解:(2)∵AC=BC=CD(已知)
∴∠B=∠BAC,∠D=∠DAC(等边对等角)
∵AB=AD(已证)
∴∠B=∠D(等边对等角)
∴∠B=∠BAC=∠D=∠DAC
∵∠B+∠BAC+∠D+∠DAC=180°(三角形内角和定理)
∴∠BAC=∠DAC=45°,∴∠BAD=90°
四、随堂检测
1.B
2.D
3.C
4.D
5.B
6.800,200.
7.(1)∵AC⊥BD,AC=BC=CD,
∴∠ACB=∠ACD=90°.
∴△ACB≌△ACD.
∴AB=AD.
∴△ABD是等腰三角形.
(2)∵AC⊥BD,AC=BC=CD,
∴△ACB、△ACD都是等腰直角三角形.
∴∠B=∠D=45°.
∴∠BAD=90°.
导学案
学习目标
1、探索证明等腰三角形性质定理的思路与方法。
2、掌握证明的基本要求和方法。
学习重点:探索证明等腰三角形性质定理的思路与方法。
学习难点:掌握证明的基本要求和方法。
一、自学释疑
探索证明等腰三角形性质定理的过程中,应该注意些什么?
二、思学质疑
把你在本次课程学习中的困惑与建议填写在下面,与同学交流后,由组长整理后并拍照上传平台讨论区。
__________________________________________________________________________________________________________________________________________
三、合作探究
问题1:根据学过的基本事实和已知的定理,能证明“两角分别相等且其中一组等角的对边相等的两个三角形全等”吗?与同伴交流,展示你的说理过程。
如:已知:在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
问题2:等腰三角形有什么性质?
探究点一:等腰三角形的两个底角关系,与同伴交流。
活动1:回忆七年级下册通过什么活动获得的等腰三角形的性质?
活动2:你能证明等腰三角形的这条性质吗?
这条性质结论: .简述为: .
探究点二:回顾前面的证明过程,AD有什么性质?为什么?由此得到什么结论?与同伴交流。
这一结论简述为: .
变式训练:
1.如图,在△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1)求证:△ABD是等腰三角形;
(2)∠BAD的度数.
四、随堂检测
1.等腰三角形的一个角是80°,则它顶角的度数是( )
A.80° B.80°或20° C.80°或50° D.20°
2.已知等腰三角形的两边长分别是3和5,则该三角形的周长是( )
A.8 B.9 C.10或12 D.11或13
3.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A.7 B.11 C.7或11 D.7或10
4.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或150° D.60°或120°
5.在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
A.36° B.54° C.18 ° D.64°
6.△ABC中,AB=BD=DC,∠C=40°,则∠A=________,∠ABD=_______.
7.△ABD中,C是BD上的一点,且AC⊥BD,AC=BC=CD.
①求证:△ABD是等腰三角形
② 求∠BAD的度数.
我的收获
1、 .
2、教会学生根据已知条件选择合适的证明方法解题.
参考答案
问题1:证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°。
∴ ∠C=180°-(∠A+∠B),
∠F=180°-(∠D+∠E) 。
∵∠A=∠D,∠B=∠E ∴∠C=∠F。
∵ BC=EF,∴△ABC≌△DEF
问题2:
探究点一:活动2:证明:如图,取BC的中点为D,连接AD
∵AB=AC,BD=CD,AD=AD,
∴△ABD△≌△ACD(SSS).
∴∠B=∠C (全等三角形的对应角相等).
等腰三角形的两底角相等.等边对等角·
探究点二:
解:AD是底边上的中线,也是底边上的高,同时也是顶角的平分线;
理由如下:过顶点A作∠BAC的平分线AD,交BC于点D,
∵AD是△ABC中的角平分线,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD(全等三角形的对应边相等),
∠ADB=∠ADC(全等三角形的对应角相等).
∴AD是BC边上的中线,
∠BDA=90°,
∴AD是BC边上的高,
∴等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合。
三线合一.
变式训练:
1.证明:(1)∵AC⊥BD(已知)
∴∠ACB=∠ACD=90°(垂直定义)
△ABC与△ADC中
AC=AC
∠ACB=∠ACD
BC=DC
∴△ABC≌△ADC(SAS)
AB=AD(全等三角形对应边相等)
∴△ABD是等腰三角形(等腰三角形的定义)
解:(2)∵AC=BC=CD(已知)
∴∠B=∠BAC,∠D=∠DAC(等边对等角)
∵AB=AD(已证)
∴∠B=∠D(等边对等角)
∴∠B=∠BAC=∠D=∠DAC
∵∠B+∠BAC+∠D+∠DAC=180°(三角形内角和定理)
∴∠BAC=∠DAC=45°,∴∠BAD=90°
四、随堂检测
1.B
2.D
3.C
4.D
5.B
6.800,200.
7.(1)∵AC⊥BD,AC=BC=CD,
∴∠ACB=∠ACD=90°.
∴△ACB≌△ACD.
∴AB=AD.
∴△ABD是等腰三角形.
(2)∵AC⊥BD,AC=BC=CD,
∴△ACB、△ACD都是等腰直角三角形.
∴∠B=∠D=45°.
∴∠BAD=90°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
