2022-2023学年人教版八年级数学下册 18.1.1平行四边形的性质(1)课件 22张PPT
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册 18.1.1平行四边形的性质(1)课件 22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 374.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 15:02:17 | ||
图片预览





文档简介
(共22张PPT)
人教版八年级数学下册课件
平行四边形的性质(1)
第十八章 平行四边形
1.(2022新课标)理解平行四边形的概念.
2.(2022新课标)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等.
3.(2022新课标)理解两条平行线之间距离的概念,能度量两条平行线之间的距离.
几何直观 推理能力
模型观念 应用意识
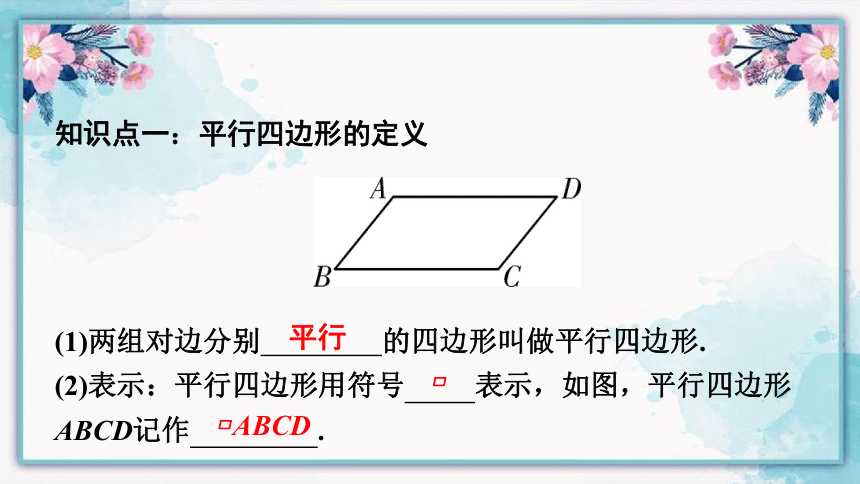
(1)两组对边分别 的四边形叫做平行四边形.
(2)表示:平行四边形用符号 表示,如图,平行四边形ABCD记作 .
ABCD
知识点一:平行四边形的定义
平行
1.如左图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ (性质).
反过来,∵AB∥CD,AD∥BC,
∴四边形ABCD是 (判定).
平行四边形
BC
DC
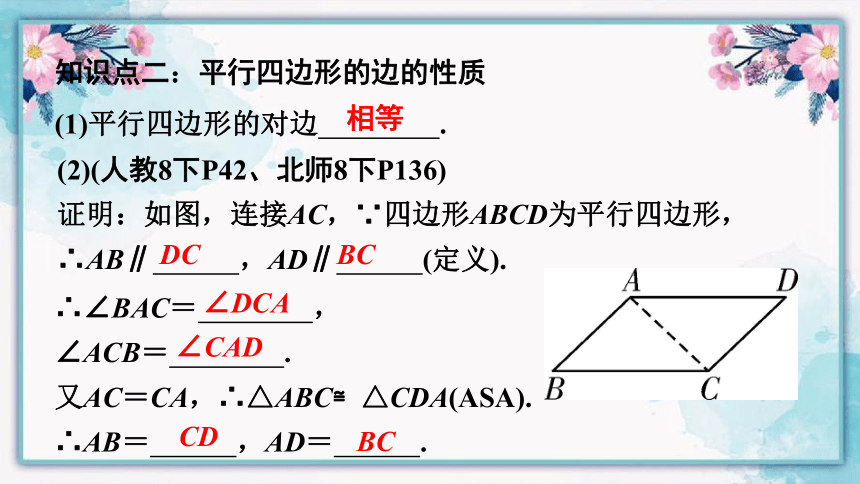
∴∠BAC= ,
∠ACB= .
又AC=CA,∴△ABC≌△CDA(ASA).
∴AB= ,AD= .
BC
CD
∠CAD
(1)平行四边形的对边 .
∠DCA
知识点二:平行四边形的边的性质
(2)(人教8下P42、北师8下P136)
证明:如图,连接AC,∵四边形ABCD为平行四边形,∴AB∥ ,AD∥ (定义).
BC
DC
相等
A.8 B.10
C.15 D.16
2.(人教8下P43、北师8下P139)如图,在 ABCD中,AB=5,BC=3,则 ABCD的周长是( )
D
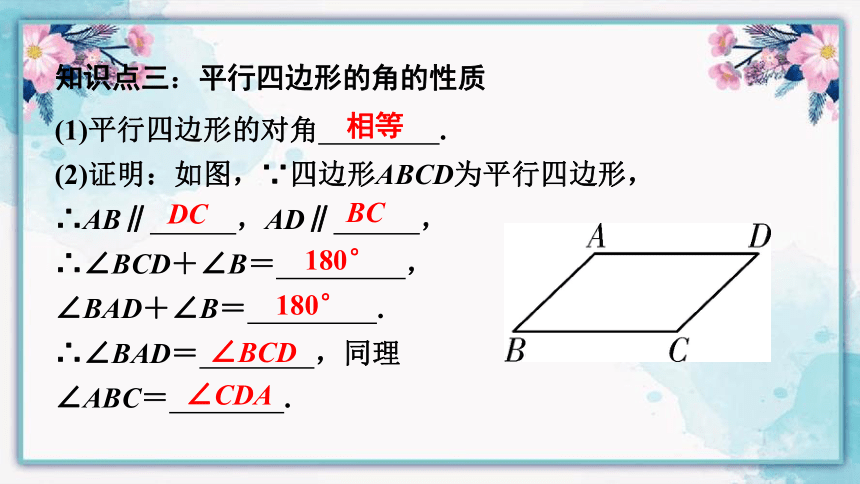
(1)平行四边形的对角 .
(2)证明:如图,∵四边形ABCD为平行四边形,
∴AB∥ ,AD∥ ,
∴∠BCD+∠B= ,
∠BAD+∠B= .
∴∠BAD= ,同理
∠ABC= .
∠CDA
∠BCD
180°
180°
BC
DC
知识点三:平行四边形的角的性质
相等
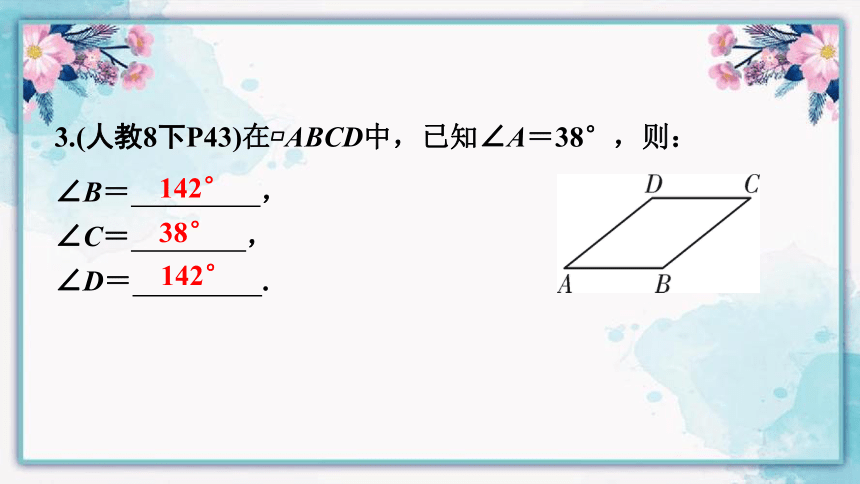
∠B= ,
∠C= ,
∠D= .
142°
38°
3.(人教8下P43)在 ABCD中,已知∠A=38°,则:
142°
(1)两条平行线之间的任意两条平行线段 .
(2)两条平行线中,一条直线上 一点到另一条直线的距离,叫做这两条平行线之间的距离.如图,已知a∥b,则a与b之间的距离就是图中线段 的长度.
CD
任意
知识点四:两条平行线之间的距离
都相等
A.AB=CD
B.EC=GF
C.A,B两点的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
4.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法不正确的是( )
D
5.【例1】(北师8下P136)如图,在 ABCD中,点E,F在对角线BD上,BE=DF,求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF,∴AE=CF.
小结:在平行四边形中证明线段与角的问题通常要用到全等.
6.【例2】(人教8下P42、北师8下P168)如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC.
在△DEA和△BFC中,,
∴△DEA≌△BFC,∴AE=CF.
小结:掌握平行四边形的性质是解题关键.
7.【例3】如图,在 ABCD中,DE平分∠ADC交BC于E,求证:△DCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠3,
∵DE平分∠ADC,
∴∠1=∠2, ∴∠3=∠2,
∴△DCE是等腰三角形.
小结:(解题模型)平行线+角平分线→等腰三角形.
小结:平移法求点的坐标.
8.【例4】(2022泰安)如图,四边形ABCD为平行四边形,则点B的坐标为 .
(-2,-1)
9.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:∠BAE=∠DCF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF.∴∠BAE=∠DCF.
10.(人教8下P43、北师8下P159)如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形.转动其中一张纸条,线段AD和BC的长度有什么关系 为什么
解:AD=BC,理由如下:
由条件可知AB∥CD,
AD∥BC,
∴四边形ABCD为平行四边形,∴AD=BC.
11.(2022贵阳模拟)如图,在 ABCD中,CD=10,BC=12,AF,DE分别平分∠BAD,∠ADC,交BC于F,E.求EF的长.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=10,BC=AD=12,
∴∠DAF=∠AFB,∠ADE=∠CED,
∵AF,DE分别平分∠BAD,∠ADC,
∴∠DAF=∠BAF,∠ADE=∠CDE,
∴∠BAF=∠AFB,∠CDE=∠CED,
∴AB=BF,CD=CE,∴BF=CE=10,
∴EF=BF+CE-BC=10+10-12=8.
★12.已知平行四边形的顶点O(0,0),A(3,1),C(1,2),直接写出第四个顶点B的坐标.
解:OA为对角线时,四边形COBA是平行四边形,顶点B的坐标是(2,-1);
OC为对角线时,四边形OBCA是平行四边形,顶点B的坐标是(-2,1);
AC为对角线时,四边形OCBA是平行四边形,顶点B的坐标是(4,3).
谢谢大家!
人教版八年级数学下册课件
平行四边形的性质(1)
第十八章 平行四边形
1.(2022新课标)理解平行四边形的概念.
2.(2022新课标)探索并证明平行四边形的性质定理:平行四边形的对边相等、对角相等.
3.(2022新课标)理解两条平行线之间距离的概念,能度量两条平行线之间的距离.
几何直观 推理能力
模型观念 应用意识
(1)两组对边分别 的四边形叫做平行四边形.
(2)表示:平行四边形用符号 表示,如图,平行四边形ABCD记作 .
ABCD
知识点一:平行四边形的定义
平行
1.如左图,∵四边形ABCD是平行四边形,
∴AB∥ ,AD∥ (性质).
反过来,∵AB∥CD,AD∥BC,
∴四边形ABCD是 (判定).
平行四边形
BC
DC
∴∠BAC= ,
∠ACB= .
又AC=CA,∴△ABC≌△CDA(ASA).
∴AB= ,AD= .
BC
CD
∠CAD
(1)平行四边形的对边 .
∠DCA
知识点二:平行四边形的边的性质
(2)(人教8下P42、北师8下P136)
证明:如图,连接AC,∵四边形ABCD为平行四边形,∴AB∥ ,AD∥ (定义).
BC
DC
相等
A.8 B.10
C.15 D.16
2.(人教8下P43、北师8下P139)如图,在 ABCD中,AB=5,BC=3,则 ABCD的周长是( )
D
(1)平行四边形的对角 .
(2)证明:如图,∵四边形ABCD为平行四边形,
∴AB∥ ,AD∥ ,
∴∠BCD+∠B= ,
∠BAD+∠B= .
∴∠BAD= ,同理
∠ABC= .
∠CDA
∠BCD
180°
180°
BC
DC
知识点三:平行四边形的角的性质
相等
∠B= ,
∠C= ,
∠D= .
142°
38°
3.(人教8下P43)在 ABCD中,已知∠A=38°,则:
142°
(1)两条平行线之间的任意两条平行线段 .
(2)两条平行线中,一条直线上 一点到另一条直线的距离,叫做这两条平行线之间的距离.如图,已知a∥b,则a与b之间的距离就是图中线段 的长度.
CD
任意
知识点四:两条平行线之间的距离
都相等
A.AB=CD
B.EC=GF
C.A,B两点的距离就是线段AB的长度
D.a与b的距离就是线段CD的长度
4.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法不正确的是( )
D
5.【例1】(北师8下P136)如图,在 ABCD中,点E,F在对角线BD上,BE=DF,求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF,∴AE=CF.
小结:在平行四边形中证明线段与角的问题通常要用到全等.
6.【例2】(人教8下P42、北师8下P168)如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF.
证明:∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C.
∵DE⊥AB,BF⊥CD,
∴∠DEA=∠BFC.
在△DEA和△BFC中,,
∴△DEA≌△BFC,∴AE=CF.
小结:掌握平行四边形的性质是解题关键.
7.【例3】如图,在 ABCD中,DE平分∠ADC交BC于E,求证:△DCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠3,
∵DE平分∠ADC,
∴∠1=∠2, ∴∠3=∠2,
∴△DCE是等腰三角形.
小结:(解题模型)平行线+角平分线→等腰三角形.
小结:平移法求点的坐标.
8.【例4】(2022泰安)如图,四边形ABCD为平行四边形,则点B的坐标为 .
(-2,-1)
9.如图,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:∠BAE=∠DCF.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴△ABE≌△CDF.∴∠BAE=∠DCF.
10.(人教8下P43、北师8下P159)如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形.转动其中一张纸条,线段AD和BC的长度有什么关系 为什么
解:AD=BC,理由如下:
由条件可知AB∥CD,
AD∥BC,
∴四边形ABCD为平行四边形,∴AD=BC.
11.(2022贵阳模拟)如图,在 ABCD中,CD=10,BC=12,AF,DE分别平分∠BAD,∠ADC,交BC于F,E.求EF的长.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=10,BC=AD=12,
∴∠DAF=∠AFB,∠ADE=∠CED,
∵AF,DE分别平分∠BAD,∠ADC,
∴∠DAF=∠BAF,∠ADE=∠CDE,
∴∠BAF=∠AFB,∠CDE=∠CED,
∴AB=BF,CD=CE,∴BF=CE=10,
∴EF=BF+CE-BC=10+10-12=8.
★12.已知平行四边形的顶点O(0,0),A(3,1),C(1,2),直接写出第四个顶点B的坐标.
解:OA为对角线时,四边形COBA是平行四边形,顶点B的坐标是(2,-1);
OC为对角线时,四边形OBCA是平行四边形,顶点B的坐标是(-2,1);
AC为对角线时,四边形OCBA是平行四边形,顶点B的坐标是(4,3).
谢谢大家!
