画相似图形[下学期]

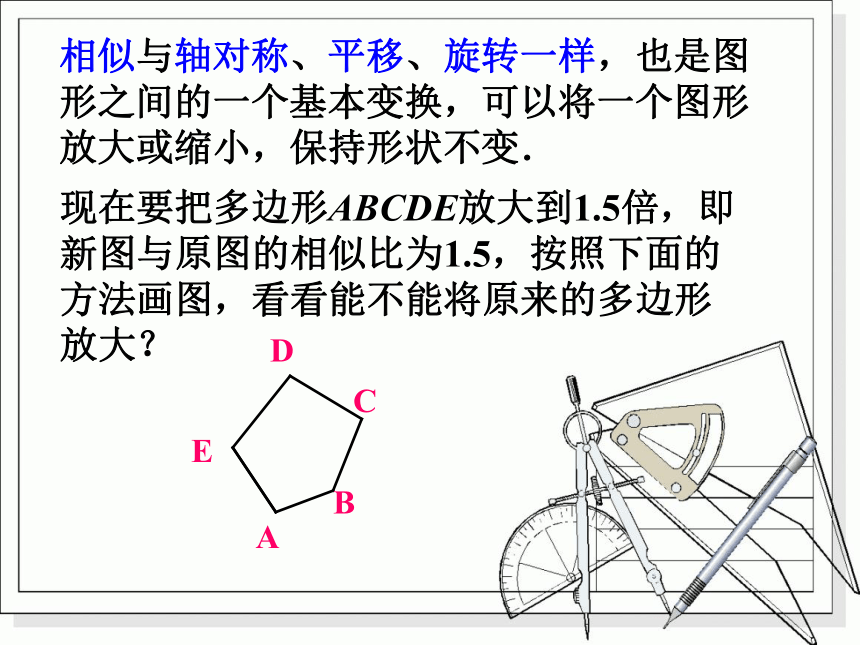
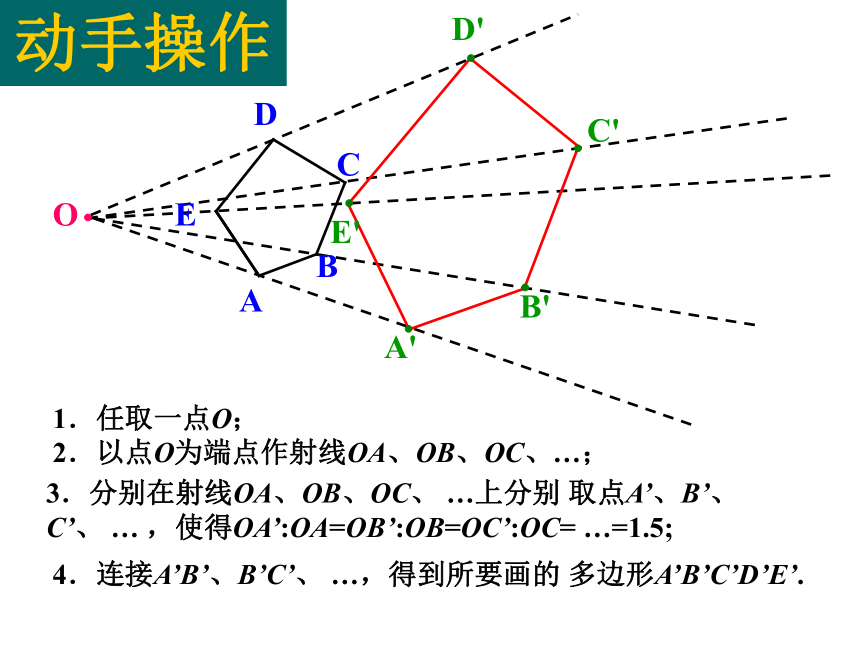
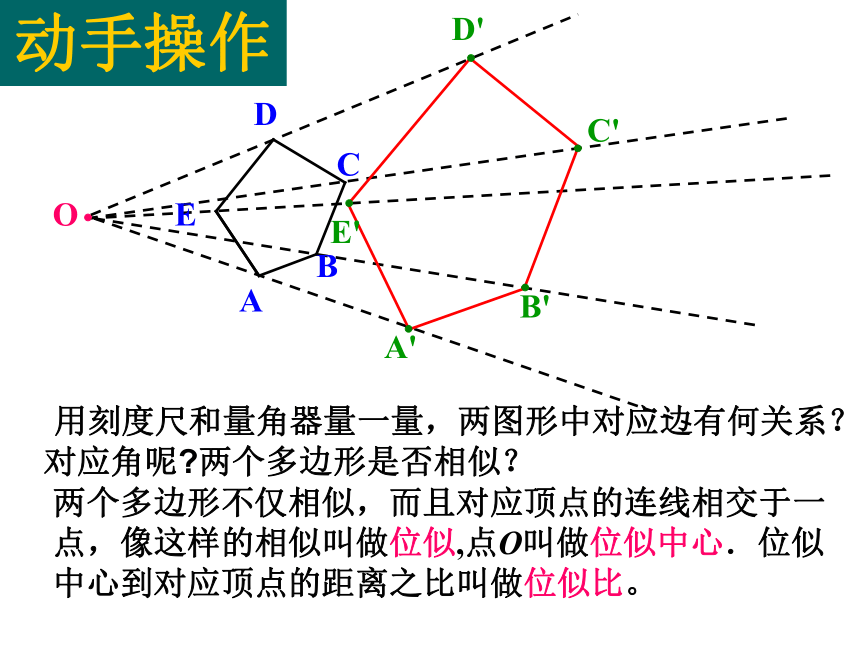
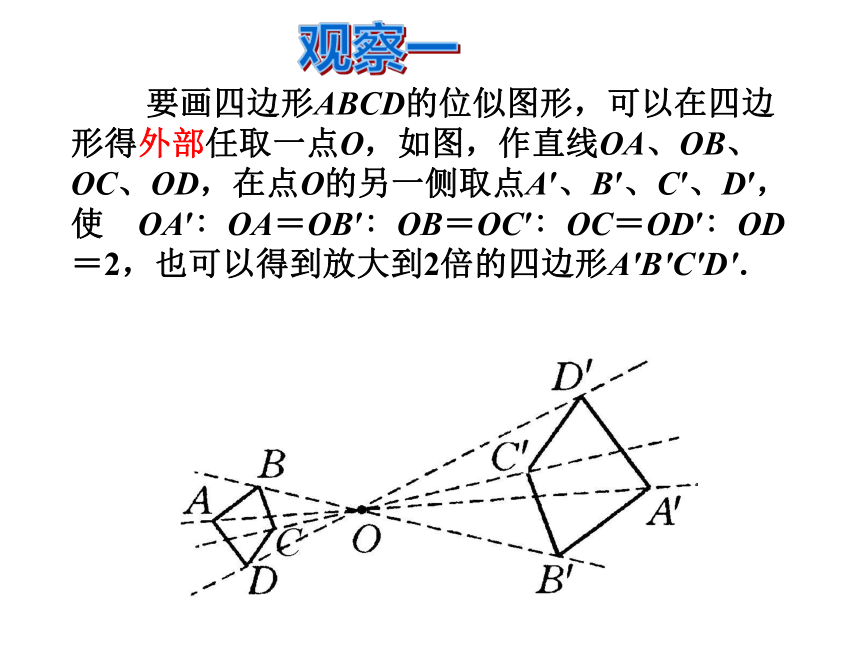
课件18张PPT。§18.4 画相似图形相似与轴对称、平移、旋转一样，也是图形之间的一个基本变换，可以将一个图形放大或缩小，保持形状不变．现在要把多边形ABCDE放大到1.5倍，即新图与原图的相似比为1.5，按照下面的方法画图，看看能不能将原来的多边形放大？1．任取一点O；2．以点O为端点作射线OA、OB、OC、…；3．分别在射线OA、OB、OC、 …上分别 取点A’、B’、 C’、 … ，使得OA’:OA=OB’:OB=OC’:OC= …=1.5;4．连接A’B’、B’C’、 …，得到所要画的 多边形A’B’C’D’E’.动手操作动手操作 用刻度尺和量角器量一量，两图形中对应边有何关系？对应角呢?两个多边形是否相似？两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的相似叫做位似,点O叫做位似中心．位似中心到对应顶点的距离之比叫做位似比。放电影时，胶片和屏幕上的画面就形成了一种位似关系． 要画四边形ABCD的位似图形，可以在四边形得外部任取一点O，如图，作直线OA、OB、OC、OD，在点O的另一侧取点A′、B′、C′、D′，使 OA′∶OA＝OB′∶OB＝OC′∶OC＝OD′∶OD＝2，也可以得到放大到2倍的四边形A′B′C′D′．观察一幻灯机的胶片和屏幕上的画面也形成一种位似关系．观察二 如图所示，画多边形的位似图形，如果把位似中心取在多边形内部，那么也可以把一个多边形放大或缩小，而且较为简便．如图，作⊿ABC的位似图形，如果选取A点为位似中心，位似比为1：2，作图过程是：延长CA到C’，使AC’ = ，延长BA到B’，使 ，连结 ，则 与⊿ ABC是位似图形。自己动手练一下进行位似变换时，位似中心可以在图形的内部、外部的任意一点 ，也可以是图形边上的一点或是顶点。C’B’1、如图，工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片，先用正方形模板在ΔABC内画一个正方形，然后过正方形在三角形内的一个顶点画射线交边AC于点G，再作GF⊥BC，F为垂足，GD∥BC交AB于D， DE⊥BC， E为垂足，则四边形DEFG就是最大的正方形，这里用到了两个正方形位似的问题，它们的位似中心是_______。AGFEDCB练习2、由位似变换得到的图形与原图形是（ ）
A，全等 B ，相似 C，不一定相似 D ，肯定不全等。3、如图， ΔABC是ΔDEF经过位似变换得到的，位似比为3：2，若AD=4cm,AB=5cm，则：OA=________,DE=________。B8cm7.5cm练习4、已知⊿ABC，以点A为位似中心，作出⊿ ADE，使⊿ ADE是⊿ ABC放大2倍的图形，这样的图形可以作出 个，它们之间的关系是 。5、将一个多边形放大为原来的3倍，则放大后的图形可作出 个，其原因是 。6、把甲图放大为原来的1.5倍得乙图，再把乙图缩小 ? 得丙图，则甲图与丙图的相似比为 。练习7、如图，是由正三角形A经过一些变换得到的，其中的变换不包含（ ）
A平移 B旋转 C位似变换 D轴对称练习8、利用位似变换把多边形ABCDEF放大到原来的2倍，则下列结论正确的是（ ）
A新图形与原图形的对应边之比是2
B新图形与原图形的对应角之比是2
C新图形与原图形的面积之比是2
D新图形与原图形的边数之比是2练习9、关于位似变换，
（1）由位似变换得到的图形与原来的图形是相似的图形；
（2）两个图形的对应顶点的连线都经过位似中心；
（3）两个图形的对应边平行或经过位似中心；
（4）位似中心可以取在任意位置。
上述结论正确的个数是（ ）
A1个 B2个 C3个 D4个练习小结1、位似的概念，所画出的图形应与原图形相似，
按照一定的比例缩放，同时应注意的是位似图形的对应顶点连线必交于一点，这一点即为位似中心。2、画位似图形的关键是确定位似中心。先连结顶点与位似中心，然后按比例确定对应点的位置，再连结对应点即可作出相应的位似图形。3、根据位似画出的图形是非常美观的，在实际生活中有着一定的应用。感悟与反思前面，我们所画的 两个多边形不仅相似，而且对应顶点的连线相交于一点，像这样的相似叫做位似,点O叫做位似中心．进行位似变换后所得到的图形与原图形相似，对应顶点的连线都经过位似中心。利用位似的方法，可以把一个多边形放大或缩小． 4.如图，AB与CD交于O,AC∥BD,若CO：CD= 1：4，AC=2cm，则BD= cm；
A C A
O E F
D B B C
5．如图，△ABC中，EF∥BC，EF:BC=1:3且BF与CE相交于O，则FO:BO= ；