相似三角形[下学期]
图片预览



文档简介
(共15张PPT)
相似三角形
18章
回顾与反思
1、相似多边形的特征是什么?
2、如何判断两个多边形是否相似?
3、相似多边形中最简单的是什么?你可以给出相应的定义吗?
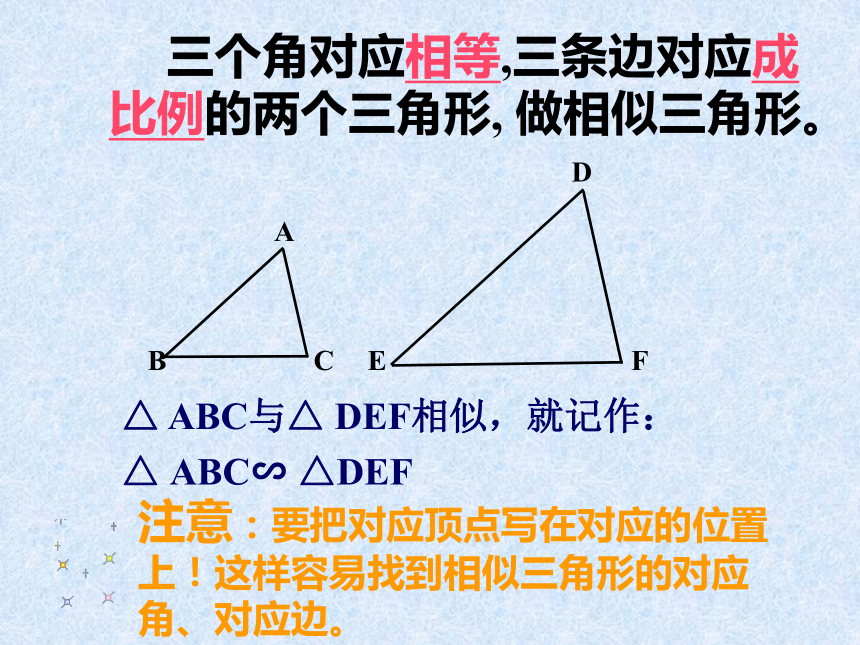
三个角对应相等,三条边对应成比例的两个三角形, 做相似三角形。
A
B
C
D
E
F
△ ABC与△ DEF相似,就记作:
△ ABC∽ △DEF
注意:要把对应顶点写在对应的位置上!这样容易找到相似三角形的对应角、对应边。
基本性质:相似三角形的各对应角相等,各对应边对应成比例。
A
B
C
D
E
F
如果△ ABC∽ △DEF,那么
∠A = ∠D,∠B = ∠E,∠C = ∠F.
= k
这个比值k表示这两个相似三角形的相似比。
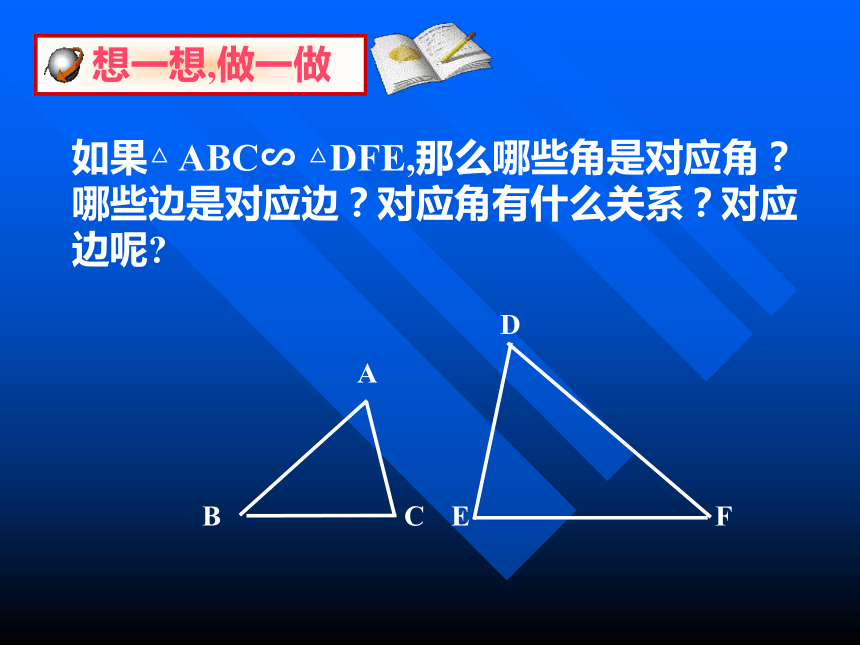
如果△ ABC∽ △DFE,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢
A
B
C
D
E
F
想一想,做一做
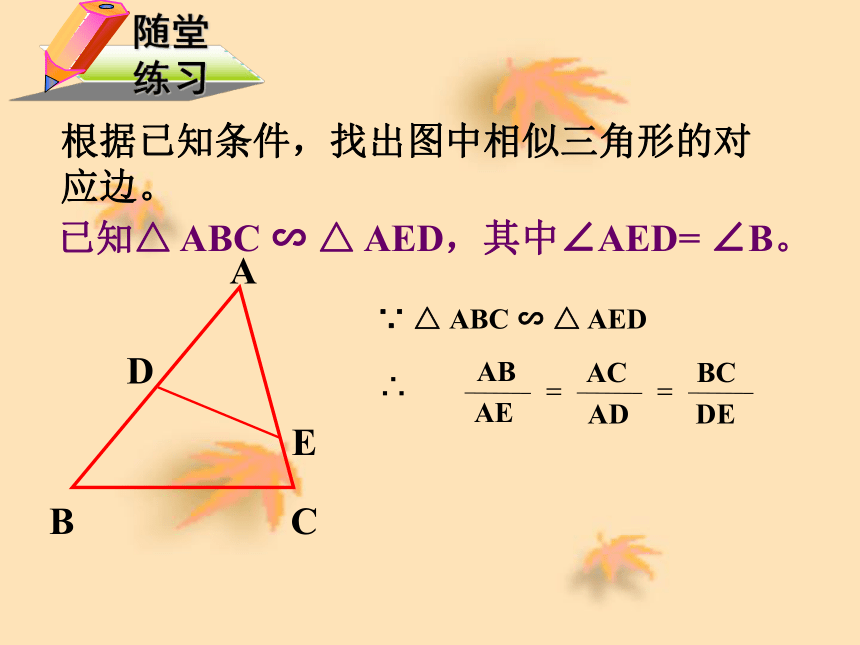
根据已知条件,找出图中相似三角形的对应边。
已知△ ABC ∽ △ AED,其中∠AED= ∠B。
A
B
C
D
E
∴
∵ △ ABC ∽ △ AED
DE
BC
AD
AC
AE
AB
=
=
随堂练习
做一做
A
B
C
D
E
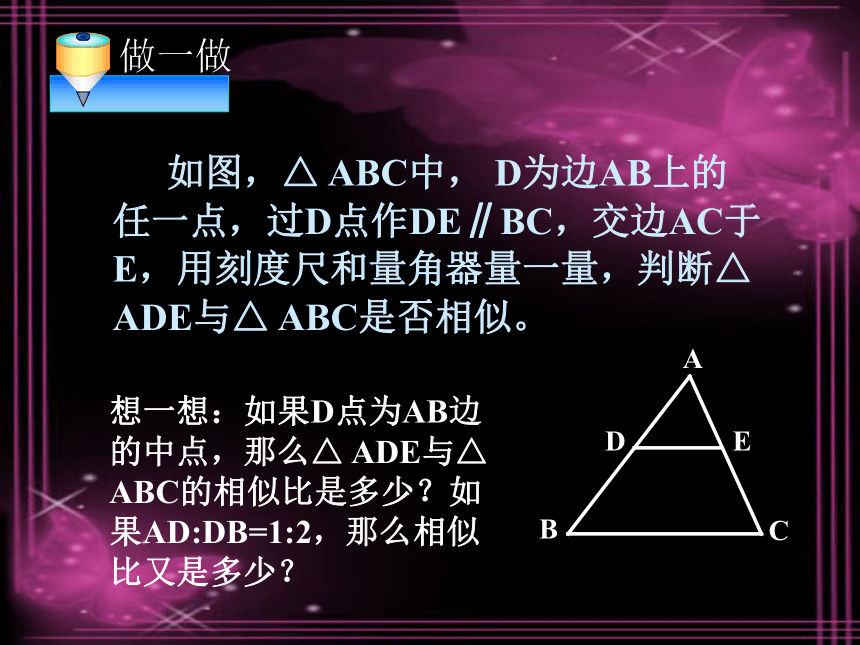
如图,△ ABC中, D为边AB上的任一点,过D点作DE∥BC,交边AC于E,用刻度尺和量角器量一量,判断△ ADE与△ ABC是否相似。
想一想:如果D点为AB边的中点,那么△ ADE与△ ABC的相似比是多少?如果AD:DB=1:2,那么相似比又是多少?
探索:
我们可以怎样判断两个三角形是否相似?
观察你们同伴间的三角板,同样角度的三角板是不是相似的?量一量他们的边,由此,你可以得到什么结论吗?
识别三角形相似的方法之一
两角对应相等的两个三角形相似.
如图,在△ ABC和△ DEF中
如果∠A=∠D, ∠B=∠E,
交流讨论
A
B
C
D
E
F
那么△ ABC∽ △DEF
想一想:如果两个三角形仅一对角对应相等,那么它们一定相似吗?如果不相似,你能举出反例吗?
例题:
例1 如图18.3.4所示,在两个直角三角形△ABC 和△A′B′C′中,
∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似.
例题:
例2 如图18.3.5,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC(已知),
∠AED=∠C. (两直线平行,同位角相等)
∴ △ADE∽△EFC. (如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)
练习1:
A
B
C
D
E
图1
图2
A
B
D
E
C
如图:已知ED∥BC,那么△ABC与△ADE相似吗?
练习:
A
B
C
D
E
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.
小结 拓展
想一想,相似比等于1的两个三角形会是什么样的关系?
相似三角形
18章
回顾与反思
1、相似多边形的特征是什么?
2、如何判断两个多边形是否相似?
3、相似多边形中最简单的是什么?你可以给出相应的定义吗?
三个角对应相等,三条边对应成比例的两个三角形, 做相似三角形。
A
B
C
D
E
F
△ ABC与△ DEF相似,就记作:
△ ABC∽ △DEF
注意:要把对应顶点写在对应的位置上!这样容易找到相似三角形的对应角、对应边。
基本性质:相似三角形的各对应角相等,各对应边对应成比例。
A
B
C
D
E
F
如果△ ABC∽ △DEF,那么
∠A = ∠D,∠B = ∠E,∠C = ∠F.
= k
这个比值k表示这两个相似三角形的相似比。
如果△ ABC∽ △DFE,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边呢
A
B
C
D
E
F
想一想,做一做
根据已知条件,找出图中相似三角形的对应边。
已知△ ABC ∽ △ AED,其中∠AED= ∠B。
A
B
C
D
E
∴
∵ △ ABC ∽ △ AED
DE
BC
AD
AC
AE
AB
=
=
随堂练习
做一做
A
B
C
D
E
如图,△ ABC中, D为边AB上的任一点,过D点作DE∥BC,交边AC于E,用刻度尺和量角器量一量,判断△ ADE与△ ABC是否相似。
想一想:如果D点为AB边的中点,那么△ ADE与△ ABC的相似比是多少?如果AD:DB=1:2,那么相似比又是多少?
探索:
我们可以怎样判断两个三角形是否相似?
观察你们同伴间的三角板,同样角度的三角板是不是相似的?量一量他们的边,由此,你可以得到什么结论吗?
识别三角形相似的方法之一
两角对应相等的两个三角形相似.
如图,在△ ABC和△ DEF中
如果∠A=∠D, ∠B=∠E,
交流讨论
A
B
C
D
E
F
那么△ ABC∽ △DEF
想一想:如果两个三角形仅一对角对应相等,那么它们一定相似吗?如果不相似,你能举出反例吗?
例题:
例1 如图18.3.4所示,在两个直角三角形△ABC 和△A′B′C′中,
∠B=∠B′=90°,∠A=∠A′,
判断这两个三角形是否相似.
例题:
例2 如图18.3.5,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC.
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC(已知),
∠AED=∠C. (两直线平行,同位角相等)
∴ △ADE∽△EFC. (如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似.)
练习1:
A
B
C
D
E
图1
图2
A
B
D
E
C
如图:已知ED∥BC,那么△ABC与△ADE相似吗?
练习:
A
B
C
D
E
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.
小结 拓展
想一想,相似比等于1的两个三角形会是什么样的关系?
