2021-2022学年四川省七年级下学期人教版数学第七章:平面直角坐标系练习题期末试题选编(含解析)
文档属性
| 名称 | 2021-2022学年四川省七年级下学期人教版数学第七章:平面直角坐标系练习题期末试题选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 793.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 20:37:05 | ||
图片预览




文档简介
第七章:平面直角坐标系
一、单选题
1.(2022春·四川广元·七年级统考期末)点M在第四象限,它到x轴、y轴的距离分别是3、4,则点M的坐标是( )
A. B. C. D.
2.(2022春·四川泸州·七年级统考期末)若点P(a,b)在第四象限,则点P到x轴的距离是( )
A.a B.-a C.b D.-b
3.(2022春·四川广元·七年级统考期末)下列各点中,在第四象限且到轴的距离为个单位长度的点是( )
A. B. C. D.
4.(2022春·四川泸州·七年级统考期末)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·四川南充·七年级统考期末)如图,科考队探测到目标位于图中阴影区域内,则目标的坐标可能是( )
A. B. C. D.
6.(2022春·四川广元·七年级统考期末)在平面直角坐标系中,若点在y轴的负半轴上,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2022春·四川凉山·七年级统考期末)已知点P(a+5,a-1)在第四象限,且到x轴的距离为2,则点P的坐标为( )
A.(4,-2) B.(-4,2) C.(-2,4) D.(2,-4)
8.(2022春·四川泸州·七年级统考期末)已知点A(﹣3,2)与点B(x,y)在同一条平行y轴的直线上,且B点到x轴的矩离等于3,则B点的坐标是( )
A.(﹣3,3) B.(3,﹣3) C.(﹣3,3)或(﹣3,﹣3) D.(﹣3,3)或(3,﹣3)
9.(2022春·四川泸州·七年级统考期末)在平面直角坐标系中,对于点P(x,y),我们把点叫做点P伴随点.已知点的伴随点为,的伴随点为,点的伴随点,…,这样依次得到点,,,…,,…若点的坐标为(2,4),点的坐标为( )
A.(3,-1) B.(-2,-2) C.(-3,3) D.(2,4)
10.(2022春·四川德阳·七年级统考期末)如图,已知四边形ABCD的顶点为,,,,点M和点N同时从点出发作顺时针运动,点M的速度为1个单位每秒,点N的速度为4个单位每秒,那么点N第2024次追上点M时的坐标为( )
A. B. C. D.
11.(2022春·四川广安·七年级统考期末)如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A.(1,3) B.(5,3) C.(6,1) D.(8,2)
12.(2022春·四川南充·七年级统考期末)如图,第二象限有两点,将线段AB平移,使点A,B分别落在两条坐标轴上,则平移后点B的对应点的坐标是( )
A.或 B.或
C.或 D.或
二、填空题
13.(2022春·四川广安·七年级统考期末)若点M(2-a,3a+6)在坐标轴上,则点M的坐标是__________________
14.(2022春·四川广元·七年级统考期末)已知点A(3,-2),线段AB=4,轴(点B在点A右侧),那么点B的坐标为_______.
15.(2022春·四川绵阳·七年级统考期末)法国数学家笛卡尔最早引入坐标系,开始用坐标描述图形中点的位置.如图,中国象棋棋盘的一部分,若其中的坐标为,的坐标为,则的坐标为________.
16.(2022春·四川广安·七年级统考期末)在平面直角坐标系中,将点A′(﹣2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是_____.
17.(2022春·四川南充·七年级统考期末)某校教学楼在校门的正北200m处,实验楼在教学楼正西100m处,若实验楼的坐标为,则校门的坐标为_________.
三、解答题
18.(2022春·四川广元·七年级统考期末)(1)平面直角坐标系中,有一点,当点到轴距离是1时,求的值.
(2)已知,.
①已知的算术平方根为3,求的值;
②如果一个正数的平方根分别为,,求这个正数.
19.(2022春·四川自贡·七年级统考期末)如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(2,0),且满足,线段AB交y轴于点F.
(1)填空:a=______,b=______;
(2)如图1,在x轴上是否存在点P,使得△ABP的面积与△ABC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为y轴正半轴上一点,,且AM,DM分别平分∠CAB,∠ODE,AM交y轴于点P,求∠AMD度数.
20.(2022春·四川南充·七年级统考期末)如图,在直角坐标系中,点,分别在轴,轴上,且.轴,轴,,交于点,为的中点.
(1)求点的坐标.
(2)点是线段上一点(不与点,重合),用含的式子表示并求整点(横、纵坐标均为整数)的坐标.
(3)点在上(点不与,重合),,交于点,,的平分线交于点.当点P在线段上运动时,的大小是否变化?若不变,求出的度数;若变化,说明理由.
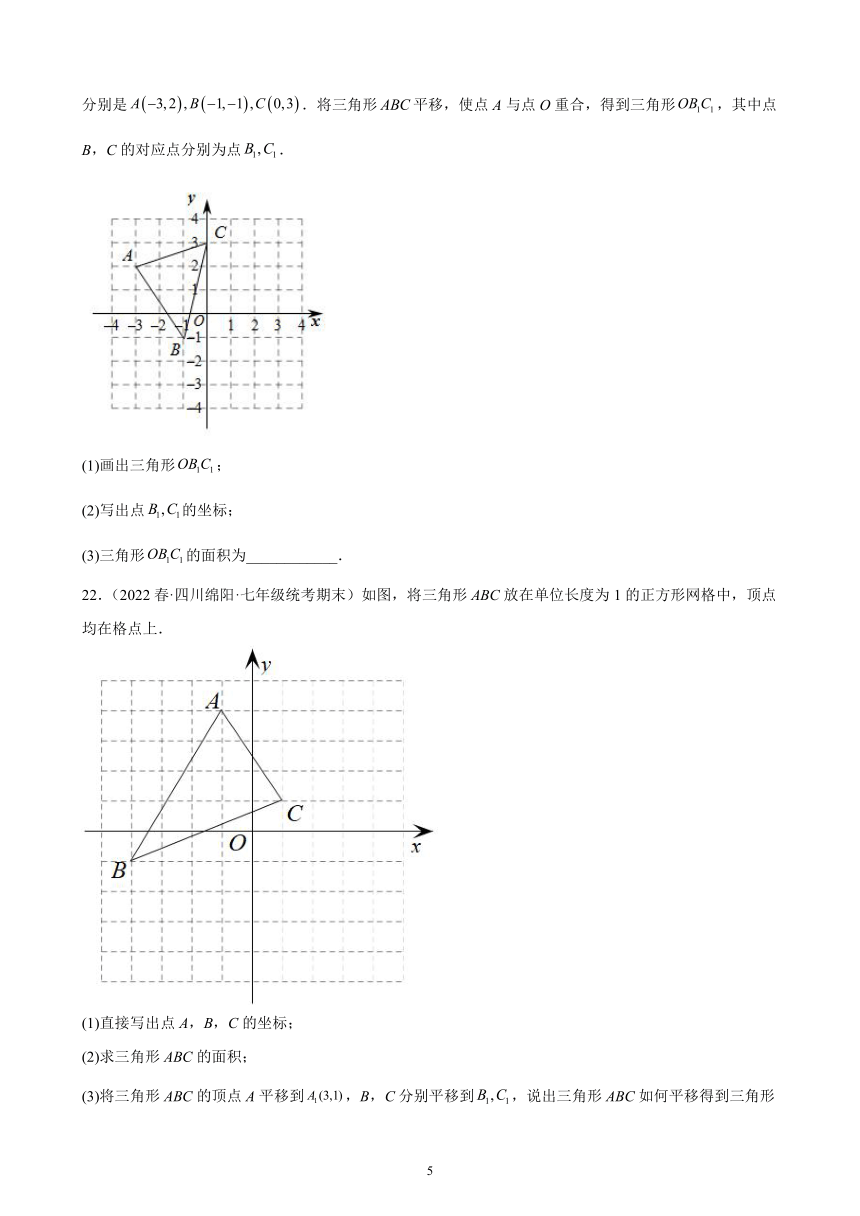
21.(2022春·四川泸州·七年级统考期末)如图,在平面直角坐标系中,三角形三个顶点的坐标分别是.将三角形平移,使点A与点O重合,得到三角形,其中点B,C的对应点分别为点.
(1)画出三角形;
(2)写出点的坐标;
(3)三角形的面积为____________.
22.(2022春·四川绵阳·七年级统考期末)如图,将三角形ABC放在单位长度为1的正方形网格中,顶点均在格点上.
(1)直接写出点A,B,C的坐标;
(2)求三角形ABC的面积;
(3)将三角形ABC的顶点A平移到,B,C分别平移到,说出三角形ABC如何平移得到三角形,并画出平移后的三角形.
23.(2022春·四川广安·七年级统考期末)如图是某市火车站及周围的平面示意图,已知超市的坐标是,市场的坐标是.
(1)根据题意,画出相应的平面直角坐标系,并在图中标出汽车站,花坛的位置;
(2)分别写出体育场、火车站和文化宫的坐标.
参考答案:
1.B
【分析】已知点M在第四象限内,那么横坐标大于0,纵坐标小于0,进而根据到坐标轴的距离判断具体坐标.
【详解】解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴、y轴的距离分别是3、4,
所以点M的坐标为(4,﹣3).
故选:B.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.D
【分析】点到x轴的距离为点的纵坐标的绝对值.
【详解】解:∵点在第四象限,
∴
∴点P到x轴的距离是
故选D.
【点睛】主要考查了点的坐标的几何意义,需注意距离为非负值.
3.B
【分析】首先确定各点所在象限,再根据到x轴的距离为3个单位进行判断.
【详解】解:A、在第三象限,故此选项不符合题意;
B、在第四象限,到轴的距离为个单位长度,故此选项符合题意;
C、在第二象限,故此选项不合题意;
D、在第四象限,到轴的距离为个单位长度,故此选项不符合题意;
故选:.
【点睛】此题主要考查了点的坐标,解题的关键是掌握四个象限内点的坐标符号.
4.C
【分析】根据点在各象限的坐标特点即可解答.
【详解】解:,点的横坐标-2<0,纵坐标-3<0,
∴这个点在第三象限.
故选C.
【点睛】解决本题的关键是记住平面直角坐标系中各个象限内点的坐标的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.D
【分析】根据第二象限中点的符号的特点可知目标的坐标可能是.
【详解】因为阴影区域在第二象限,所以x坐标为负,y坐标为正,符合要求的只有D选项.
故选:D.
【点睛】本题考查了平面直角坐标系中各个象限的点的坐标符号特点,四个象限的点的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
6.B
【分析】根据y轴负半轴上的点:横坐标=0,纵坐标<0,即可求解.
【详解】解:∵点在y轴的负半轴上,
∴,则,
∴点在第二象限,
故选B
【点睛】本题考查了判断点所在象限,求得是解题的关键.
7.A
【详解】解:由点P在第四象限,且到轴的距离为2,则点P的纵坐标为-2,
即解得
,
则点P的坐标为(4,-2).
故选:A.
【点睛】本题考查点的坐标.
8.C
【详解】已知点A(-3,2)与点B(x,y)在同一条平行y轴的直线上,可得x=-3,再由点B到x轴的距离等于3,可得|y|=3,即y=3或-3,所以点B的坐标为(-3,3)或(-3,-3).故选C.
9.D
【分析】根据伴随点的定义依次求出后面几个点,不难发现,每4个点为一个循环组,用2021除以4,得出商与余数后确定的坐标即可.
【详解】解:∵的坐标为(2,4),
∴(-3,3),(-2,-2),(3,-1),(2,4),……
依次类推,每4个为一个循环组;
∵2021÷4=505…1,
∴点的坐标与的坐标相同,为(2,4),
故选:D.
【点睛】本题是对点的变化规律的考查,读懂题目信息,理解伴随点的定义并求出每4个一组循环是解题关键.
10.B
【分析】先根据行程问题求得点N第2024次追上点M时的时间,再求得此时点N所形式的路程,然后根据点N此时的位置求得此题结果.
【详解】解:由题意得,四边形ABCD的周长为:
2[1-(-1)+2-(-2)]=2×6=12,
∴点N第2024次追上点M的时间为:
12÷(4-1)×2024=12÷3×2024=8096(秒),
1×8096÷12=674…8,
∴此时点N第2024次追上点M时的坐标为(-1,-1),
故选:B.
【点睛】此题考查了确定平面直角坐标系中点的坐标的能力,关键是能根据题意正确确定点M的位置.
11.C
【分析】直接利用已知点坐标确定平面直角坐标系,进而得出答案.
【详解】解:如图所示:“马”位于(6,1).
故选:C.
【点睛】本题考查了坐标确定位置,确定出坐标原点的位置是解题的关键.
12.C
【分析】设平移后点A、B的对应点分别是A′、B′.分两种情况进行讨论:①A′在y轴上,B′在x轴上;②A′在x轴上,B′在y轴上.
【详解】解:设平移后点A、B的对应点分别是A′、B′.
分两种情况:
①A′在y轴上,B′在x轴上,
则A′横坐标为0,B′纵坐标为0,
∵点A′与点A的横坐标的差为:,
∴,
∴点B平移后的对应点的坐标是;
②A′在x轴上,B′在y轴上,
则A′纵坐标为0,B′横坐标为0,
∵,
∴,
∴点B平移后的对应点的坐标是;
综上可知,点B平移后的对应点的坐标是或.
故选C.
【点睛】本题考查平面直角坐标系内图形的平移,掌握平移的性质是解题的关键.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
13.(0,12)或(4,0)/(4,0)或(0,12)
【分析】根据轴上的点的坐标特征分类讨论进行求解即可.
【详解】解:若点M(2-a,3a+6)在轴上,
解得,,
,
若点M(2-a,3a+6)在轴上,
,
解得,,
.
故答案为:(0,12)或(4,0).
【点睛】本题考查了坐标轴上的点的坐标特征,掌握x轴上的点的纵坐标为0,y轴上的点的横坐标为0,是解题的关键.
14.(7,-2)
【分析】根据平行于x轴的直线上的点的纵坐标相等及两点间的距离,即可求得点B的坐标.
【详解】解:∵点A的坐标为(3,-2), 轴,
∴点B的纵坐标为-2,
又∵线段AB=4,点B在点A右侧
∴点B的横坐标为3+4=7,
∴点B的坐标为(7,-2),
故答案为:(7,-2).
【点睛】本题考查了平行于x轴的直线上的点的坐标特点,两点间距离的求法,掌握平行于x轴的直线上的点的坐标特点是解决本题的关键.
15.
【分析】根据题目中马与兵的坐标,在图中确定原点在马上面三格,再向左一格的位置,然后再确定炮的位置即可.
【详解】解:∵马的坐标为,兵的坐标为,
∴炮的坐标为,
故答案为:.
【点睛】本题主要考查如何运用直角坐标系确定点的位置,正确得出原点位置是解题关键.
16.(1,1)
【分析】直接利用平移的性质分别得出平移后点的坐标得出答案.
【详解】解:∵将点A′(-2,3)向右平移3个单位长度,
∴得到(1,3),
∵再向下平移2个单位长度,
∴平移后对应的点A′的坐标是:(1,1).
故答案为(1,1).
【点睛】此题主要考查了平移,正确掌握平移规律:上加下减,左加右减,是解题关键.
17.
【分析】根据已知条件实验楼的坐标,画图分析即可得到结论.
【详解】
如图,点A表示实验楼,点B表示校门,点O表示教学楼,
∵实验楼的坐标为,教学楼在校门的正北200m处,实验楼在教学楼正西100m处,
∴校门的坐标为.
故答案为:(0,-200).
【点睛】本题考查了坐标确定位置,正确理解题意是解题的关键.
18.(1)或;(2)①,②25
【分析】(1)根据点到y轴的距离为该点横坐标的绝对值,即可求解;
(2)①利用算数平方根得定义得,由此可解;
②根据一个正数的两个平方根互为相反数得,由此可解.
【详解】解:(1)由点到轴距离是1,得,
,或,
解得或.
(2)①由的算术平方根为3,得,
,
解得;
②由,是同一个正数的两个平方根,得 ,
,
解得,
,
,
故这个正数是25.
【点睛】本题考查点到坐标轴的距离以及算术平方根、平方根等知识,熟练掌握算术平方根和平方根的定义及区别是解题的关键.
19.(1)-3,3
(2)存在,P(-8,0)
(3)45°
【分析】(1)根据非负数的性质可得,即可求得a=-3,b=3;
(2)根据,即可得出P的坐标;
(3)由AM,DM分别平分∠CAB,∠ODE,得∠BAM=∠CAM=α,∠ODM=∠EDM=β,根据三角形内角和定理得:α+90°=β+∠M,根据ED∥AB,得∠EDF=∠AFD,即2β=2α+90°,综合即可解决问题;
(1)
解:∵
∴
解得
故答案为:
(2)
解:存在,
∵△ABP的面积与△ABC的面积相等
∴
当点在点的左侧时,,
当点在点的右侧时,与点重合,
综上所述,存在点使得△ABP的面积与△ABC的面积相等
(3)
∵AM,DM分别平分∠CAB,∠ODE,
∴∠BAM=∠CAM,∠ODM=∠EDM
设∠BAM=∠CAM=α,∠ODM=∠EDM=β,
由三角形内角和为180°得:
∠PAO+∠APO+∠AOP=∠DPM+∠PDM+∠M=180°,
∴α+90°=β+∠M,
∵ED∥AB,
∴∠EDF=∠AFD,
即2β=2α+90°,
∴β-α=45°,
∴∠M=90°+α-β=90°-45°=45°;
【点睛】本题考查了非负数的性质,平行线的性质与判定,坐标与图形,三角形内角和定理的应用,综合运用以上知识是解题的关键.
20.(1)
(2),
(3)不变,
【分析】(1)由非负数的性质得出,,解一元一次方程即可得出结论;
(2)由三角形面积得出,则得出,由题意求出,,则可得出答案;
(3)过点作,则,由平行线的性质可证,同理,角平分线的定义得出,,则可求出答案.
【详解】(1)解:∵,,,
∴且,
∴,,
∴点的坐标为.
(2)如图,连接,
∵为的中点,
∴,
∵
∴.
∴,
∵,都为整数,且,,
∴,,
∴整点Q的坐标为.
(3)的大小不会变化,.理由如下:
过点作,
∴,
∵轴,轴轴,
∴,
∴,
∴,
∴,
∴,
∴.
即,
同理,
∵CF平分,EF平分,
∴,.
∴.
∵,
∴,
∴.
∴当点P在线段上运动时,的大小不变,的度数为.
【点睛】本题是三角形综合题,主要考查了非负数的性质,三角形的面积的计算方法,平行公理的推论,平行线的性质,角平分线的定义等知识.熟练掌握平行线的性质是解题的关键.
21.(1)画图见解析
(2)
(3)
【分析】(1)先根据平移的性质画出点,,再顺次连接点,,即可得;
(2)根据点在平面直角坐标系中的位置即可得;
(3)利用一个长方形的面积减去三个直角三角形的面积即可得.
【详解】(1)解:如图,三角形即为所求.
(2)解:由图可知,.
(3)解:三角形的面积为:,
故答案为:.
【点睛】本题考查了平移作图、点的坐标、坐标与图形,熟练掌握平移作图的方法是解题关键.
22.(1)
(2)
(3)画图见解析
【分析】(1)直接读出点的坐标即可;
(2)将三角形ABC的面积转化为即可得出答案;
(3)由点平移到,可知图像的平移是:将三个顶点分别向右平移4个单位,再向下平移3个单位得到其对应点,继而首尾顺次连接即可.
(1)解:,
(2)如图:∴===;
(3)∵点平移到,∴图像的平移是:将三个顶点分别向右平移4个单位,再向下平移3个单位得到其对应点继而首尾顺次连接即可得到.∴如图所示:为所求.
【点睛】此题主要考查坐标与图形变化—平移,画平移图形,求三角形面积,解题的关键是熟知坐标平移的特点.
23.(1)见解析
(2)体育场(-4,2),火车站(-1,1),文化宫(0,-2)
【分析】(1)直接利用超市和市场的坐标得出原点的位置进而得出答案;
(2)利用所建立的平面直角坐标系即可得出答案.
(1)
解:如图所示:
(2)
由平面直角坐标系知,
体育场的坐标为(-4,2),火车站的坐标为(-1,1),文化宫的坐标为(0,-2).
【点睛】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
一、单选题
1.(2022春·四川广元·七年级统考期末)点M在第四象限,它到x轴、y轴的距离分别是3、4,则点M的坐标是( )
A. B. C. D.
2.(2022春·四川泸州·七年级统考期末)若点P(a,b)在第四象限,则点P到x轴的距离是( )
A.a B.-a C.b D.-b
3.(2022春·四川广元·七年级统考期末)下列各点中,在第四象限且到轴的距离为个单位长度的点是( )
A. B. C. D.
4.(2022春·四川泸州·七年级统考期末)在平面直角坐标系中,点所在的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·四川南充·七年级统考期末)如图,科考队探测到目标位于图中阴影区域内,则目标的坐标可能是( )
A. B. C. D.
6.(2022春·四川广元·七年级统考期末)在平面直角坐标系中,若点在y轴的负半轴上,则点的位置在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2022春·四川凉山·七年级统考期末)已知点P(a+5,a-1)在第四象限,且到x轴的距离为2,则点P的坐标为( )
A.(4,-2) B.(-4,2) C.(-2,4) D.(2,-4)
8.(2022春·四川泸州·七年级统考期末)已知点A(﹣3,2)与点B(x,y)在同一条平行y轴的直线上,且B点到x轴的矩离等于3,则B点的坐标是( )
A.(﹣3,3) B.(3,﹣3) C.(﹣3,3)或(﹣3,﹣3) D.(﹣3,3)或(3,﹣3)
9.(2022春·四川泸州·七年级统考期末)在平面直角坐标系中,对于点P(x,y),我们把点叫做点P伴随点.已知点的伴随点为,的伴随点为,点的伴随点,…,这样依次得到点,,,…,,…若点的坐标为(2,4),点的坐标为( )
A.(3,-1) B.(-2,-2) C.(-3,3) D.(2,4)
10.(2022春·四川德阳·七年级统考期末)如图,已知四边形ABCD的顶点为,,,,点M和点N同时从点出发作顺时针运动,点M的速度为1个单位每秒,点N的速度为4个单位每秒,那么点N第2024次追上点M时的坐标为( )
A. B. C. D.
11.(2022春·四川广安·七年级统考期末)如图,象棋盘上,若“将”位于点(3,﹣2),“车”位于点(﹣1,﹣2),则“马”位于( )
A.(1,3) B.(5,3) C.(6,1) D.(8,2)
12.(2022春·四川南充·七年级统考期末)如图,第二象限有两点,将线段AB平移,使点A,B分别落在两条坐标轴上,则平移后点B的对应点的坐标是( )
A.或 B.或
C.或 D.或
二、填空题
13.(2022春·四川广安·七年级统考期末)若点M(2-a,3a+6)在坐标轴上,则点M的坐标是__________________
14.(2022春·四川广元·七年级统考期末)已知点A(3,-2),线段AB=4,轴(点B在点A右侧),那么点B的坐标为_______.
15.(2022春·四川绵阳·七年级统考期末)法国数学家笛卡尔最早引入坐标系,开始用坐标描述图形中点的位置.如图,中国象棋棋盘的一部分,若其中的坐标为,的坐标为,则的坐标为________.
16.(2022春·四川广安·七年级统考期末)在平面直角坐标系中,将点A′(﹣2,3)向右平移3个单位长度,再向下平移2个单位长度,那么平移后对应的点A′的坐标是_____.
17.(2022春·四川南充·七年级统考期末)某校教学楼在校门的正北200m处,实验楼在教学楼正西100m处,若实验楼的坐标为,则校门的坐标为_________.
三、解答题
18.(2022春·四川广元·七年级统考期末)(1)平面直角坐标系中,有一点,当点到轴距离是1时,求的值.
(2)已知,.
①已知的算术平方根为3,求的值;
②如果一个正数的平方根分别为,,求这个正数.
19.(2022春·四川自贡·七年级统考期末)如图1,在平面直角坐标系中,已知A(a,0),B(b,3),C(2,0),且满足,线段AB交y轴于点F.
(1)填空:a=______,b=______;
(2)如图1,在x轴上是否存在点P,使得△ABP的面积与△ABC的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由;
(3)如图2,点D为y轴正半轴上一点,,且AM,DM分别平分∠CAB,∠ODE,AM交y轴于点P,求∠AMD度数.
20.(2022春·四川南充·七年级统考期末)如图,在直角坐标系中,点,分别在轴,轴上,且.轴,轴,,交于点,为的中点.
(1)求点的坐标.
(2)点是线段上一点(不与点,重合),用含的式子表示并求整点(横、纵坐标均为整数)的坐标.
(3)点在上(点不与,重合),,交于点,,的平分线交于点.当点P在线段上运动时,的大小是否变化?若不变,求出的度数;若变化,说明理由.
21.(2022春·四川泸州·七年级统考期末)如图,在平面直角坐标系中,三角形三个顶点的坐标分别是.将三角形平移,使点A与点O重合,得到三角形,其中点B,C的对应点分别为点.
(1)画出三角形;
(2)写出点的坐标;
(3)三角形的面积为____________.
22.(2022春·四川绵阳·七年级统考期末)如图,将三角形ABC放在单位长度为1的正方形网格中,顶点均在格点上.
(1)直接写出点A,B,C的坐标;
(2)求三角形ABC的面积;
(3)将三角形ABC的顶点A平移到,B,C分别平移到,说出三角形ABC如何平移得到三角形,并画出平移后的三角形.
23.(2022春·四川广安·七年级统考期末)如图是某市火车站及周围的平面示意图,已知超市的坐标是,市场的坐标是.
(1)根据题意,画出相应的平面直角坐标系,并在图中标出汽车站,花坛的位置;
(2)分别写出体育场、火车站和文化宫的坐标.
参考答案:
1.B
【分析】已知点M在第四象限内,那么横坐标大于0,纵坐标小于0,进而根据到坐标轴的距离判断具体坐标.
【详解】解:因为点M在第四象限,所以其横、纵坐标分别为正数、负数,
又因为点M到x轴、y轴的距离分别是3、4,
所以点M的坐标为(4,﹣3).
故选:B.
【点睛】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).
2.D
【分析】点到x轴的距离为点的纵坐标的绝对值.
【详解】解:∵点在第四象限,
∴
∴点P到x轴的距离是
故选D.
【点睛】主要考查了点的坐标的几何意义,需注意距离为非负值.
3.B
【分析】首先确定各点所在象限,再根据到x轴的距离为3个单位进行判断.
【详解】解:A、在第三象限,故此选项不符合题意;
B、在第四象限,到轴的距离为个单位长度,故此选项符合题意;
C、在第二象限,故此选项不合题意;
D、在第四象限,到轴的距离为个单位长度,故此选项不符合题意;
故选:.
【点睛】此题主要考查了点的坐标,解题的关键是掌握四个象限内点的坐标符号.
4.C
【分析】根据点在各象限的坐标特点即可解答.
【详解】解:,点的横坐标-2<0,纵坐标-3<0,
∴这个点在第三象限.
故选C.
【点睛】解决本题的关键是记住平面直角坐标系中各个象限内点的坐标的符号:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
5.D
【分析】根据第二象限中点的符号的特点可知目标的坐标可能是.
【详解】因为阴影区域在第二象限,所以x坐标为负,y坐标为正,符合要求的只有D选项.
故选:D.
【点睛】本题考查了平面直角坐标系中各个象限的点的坐标符号特点,四个象限的点的符号特点分别是:第一象限;第二象限;第三象限;第四象限.
6.B
【分析】根据y轴负半轴上的点:横坐标=0,纵坐标<0,即可求解.
【详解】解:∵点在y轴的负半轴上,
∴,则,
∴点在第二象限,
故选B
【点睛】本题考查了判断点所在象限,求得是解题的关键.
7.A
【详解】解:由点P在第四象限,且到轴的距离为2,则点P的纵坐标为-2,
即解得
,
则点P的坐标为(4,-2).
故选:A.
【点睛】本题考查点的坐标.
8.C
【详解】已知点A(-3,2)与点B(x,y)在同一条平行y轴的直线上,可得x=-3,再由点B到x轴的距离等于3,可得|y|=3,即y=3或-3,所以点B的坐标为(-3,3)或(-3,-3).故选C.
9.D
【分析】根据伴随点的定义依次求出后面几个点,不难发现,每4个点为一个循环组,用2021除以4,得出商与余数后确定的坐标即可.
【详解】解:∵的坐标为(2,4),
∴(-3,3),(-2,-2),(3,-1),(2,4),……
依次类推,每4个为一个循环组;
∵2021÷4=505…1,
∴点的坐标与的坐标相同,为(2,4),
故选:D.
【点睛】本题是对点的变化规律的考查,读懂题目信息,理解伴随点的定义并求出每4个一组循环是解题关键.
10.B
【分析】先根据行程问题求得点N第2024次追上点M时的时间,再求得此时点N所形式的路程,然后根据点N此时的位置求得此题结果.
【详解】解:由题意得,四边形ABCD的周长为:
2[1-(-1)+2-(-2)]=2×6=12,
∴点N第2024次追上点M的时间为:
12÷(4-1)×2024=12÷3×2024=8096(秒),
1×8096÷12=674…8,
∴此时点N第2024次追上点M时的坐标为(-1,-1),
故选:B.
【点睛】此题考查了确定平面直角坐标系中点的坐标的能力,关键是能根据题意正确确定点M的位置.
11.C
【分析】直接利用已知点坐标确定平面直角坐标系,进而得出答案.
【详解】解:如图所示:“马”位于(6,1).
故选:C.
【点睛】本题考查了坐标确定位置,确定出坐标原点的位置是解题的关键.
12.C
【分析】设平移后点A、B的对应点分别是A′、B′.分两种情况进行讨论:①A′在y轴上,B′在x轴上;②A′在x轴上,B′在y轴上.
【详解】解:设平移后点A、B的对应点分别是A′、B′.
分两种情况:
①A′在y轴上,B′在x轴上,
则A′横坐标为0,B′纵坐标为0,
∵点A′与点A的横坐标的差为:,
∴,
∴点B平移后的对应点的坐标是;
②A′在x轴上,B′在y轴上,
则A′纵坐标为0,B′横坐标为0,
∵,
∴,
∴点B平移后的对应点的坐标是;
综上可知,点B平移后的对应点的坐标是或.
故选C.
【点睛】本题考查平面直角坐标系内图形的平移,掌握平移的性质是解题的关键.在平面直角坐标系中,图形的平移与图形上某点的平移规律相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
13.(0,12)或(4,0)/(4,0)或(0,12)
【分析】根据轴上的点的坐标特征分类讨论进行求解即可.
【详解】解:若点M(2-a,3a+6)在轴上,
解得,,
,
若点M(2-a,3a+6)在轴上,
,
解得,,
.
故答案为:(0,12)或(4,0).
【点睛】本题考查了坐标轴上的点的坐标特征,掌握x轴上的点的纵坐标为0,y轴上的点的横坐标为0,是解题的关键.
14.(7,-2)
【分析】根据平行于x轴的直线上的点的纵坐标相等及两点间的距离,即可求得点B的坐标.
【详解】解:∵点A的坐标为(3,-2), 轴,
∴点B的纵坐标为-2,
又∵线段AB=4,点B在点A右侧
∴点B的横坐标为3+4=7,
∴点B的坐标为(7,-2),
故答案为:(7,-2).
【点睛】本题考查了平行于x轴的直线上的点的坐标特点,两点间距离的求法,掌握平行于x轴的直线上的点的坐标特点是解决本题的关键.
15.
【分析】根据题目中马与兵的坐标,在图中确定原点在马上面三格,再向左一格的位置,然后再确定炮的位置即可.
【详解】解:∵马的坐标为,兵的坐标为,
∴炮的坐标为,
故答案为:.
【点睛】本题主要考查如何运用直角坐标系确定点的位置,正确得出原点位置是解题关键.
16.(1,1)
【分析】直接利用平移的性质分别得出平移后点的坐标得出答案.
【详解】解:∵将点A′(-2,3)向右平移3个单位长度,
∴得到(1,3),
∵再向下平移2个单位长度,
∴平移后对应的点A′的坐标是:(1,1).
故答案为(1,1).
【点睛】此题主要考查了平移,正确掌握平移规律:上加下减,左加右减,是解题关键.
17.
【分析】根据已知条件实验楼的坐标,画图分析即可得到结论.
【详解】
如图,点A表示实验楼,点B表示校门,点O表示教学楼,
∵实验楼的坐标为,教学楼在校门的正北200m处,实验楼在教学楼正西100m处,
∴校门的坐标为.
故答案为:(0,-200).
【点睛】本题考查了坐标确定位置,正确理解题意是解题的关键.
18.(1)或;(2)①,②25
【分析】(1)根据点到y轴的距离为该点横坐标的绝对值,即可求解;
(2)①利用算数平方根得定义得,由此可解;
②根据一个正数的两个平方根互为相反数得,由此可解.
【详解】解:(1)由点到轴距离是1,得,
,或,
解得或.
(2)①由的算术平方根为3,得,
,
解得;
②由,是同一个正数的两个平方根,得 ,
,
解得,
,
,
故这个正数是25.
【点睛】本题考查点到坐标轴的距离以及算术平方根、平方根等知识,熟练掌握算术平方根和平方根的定义及区别是解题的关键.
19.(1)-3,3
(2)存在,P(-8,0)
(3)45°
【分析】(1)根据非负数的性质可得,即可求得a=-3,b=3;
(2)根据,即可得出P的坐标;
(3)由AM,DM分别平分∠CAB,∠ODE,得∠BAM=∠CAM=α,∠ODM=∠EDM=β,根据三角形内角和定理得:α+90°=β+∠M,根据ED∥AB,得∠EDF=∠AFD,即2β=2α+90°,综合即可解决问题;
(1)
解:∵
∴
解得
故答案为:
(2)
解:存在,
∵△ABP的面积与△ABC的面积相等
∴
当点在点的左侧时,,
当点在点的右侧时,与点重合,
综上所述,存在点使得△ABP的面积与△ABC的面积相等
(3)
∵AM,DM分别平分∠CAB,∠ODE,
∴∠BAM=∠CAM,∠ODM=∠EDM
设∠BAM=∠CAM=α,∠ODM=∠EDM=β,
由三角形内角和为180°得:
∠PAO+∠APO+∠AOP=∠DPM+∠PDM+∠M=180°,
∴α+90°=β+∠M,
∵ED∥AB,
∴∠EDF=∠AFD,
即2β=2α+90°,
∴β-α=45°,
∴∠M=90°+α-β=90°-45°=45°;
【点睛】本题考查了非负数的性质,平行线的性质与判定,坐标与图形,三角形内角和定理的应用,综合运用以上知识是解题的关键.
20.(1)
(2),
(3)不变,
【分析】(1)由非负数的性质得出,,解一元一次方程即可得出结论;
(2)由三角形面积得出,则得出,由题意求出,,则可得出答案;
(3)过点作,则,由平行线的性质可证,同理,角平分线的定义得出,,则可求出答案.
【详解】(1)解:∵,,,
∴且,
∴,,
∴点的坐标为.
(2)如图,连接,
∵为的中点,
∴,
∵
∴.
∴,
∵,都为整数,且,,
∴,,
∴整点Q的坐标为.
(3)的大小不会变化,.理由如下:
过点作,
∴,
∵轴,轴轴,
∴,
∴,
∴,
∴,
∴,
∴.
即,
同理,
∵CF平分,EF平分,
∴,.
∴.
∵,
∴,
∴.
∴当点P在线段上运动时,的大小不变,的度数为.
【点睛】本题是三角形综合题,主要考查了非负数的性质,三角形的面积的计算方法,平行公理的推论,平行线的性质,角平分线的定义等知识.熟练掌握平行线的性质是解题的关键.
21.(1)画图见解析
(2)
(3)
【分析】(1)先根据平移的性质画出点,,再顺次连接点,,即可得;
(2)根据点在平面直角坐标系中的位置即可得;
(3)利用一个长方形的面积减去三个直角三角形的面积即可得.
【详解】(1)解:如图,三角形即为所求.
(2)解:由图可知,.
(3)解:三角形的面积为:,
故答案为:.
【点睛】本题考查了平移作图、点的坐标、坐标与图形,熟练掌握平移作图的方法是解题关键.
22.(1)
(2)
(3)画图见解析
【分析】(1)直接读出点的坐标即可;
(2)将三角形ABC的面积转化为即可得出答案;
(3)由点平移到,可知图像的平移是:将三个顶点分别向右平移4个单位,再向下平移3个单位得到其对应点,继而首尾顺次连接即可.
(1)解:,
(2)如图:∴===;
(3)∵点平移到,∴图像的平移是:将三个顶点分别向右平移4个单位,再向下平移3个单位得到其对应点继而首尾顺次连接即可得到.∴如图所示:为所求.
【点睛】此题主要考查坐标与图形变化—平移,画平移图形,求三角形面积,解题的关键是熟知坐标平移的特点.
23.(1)见解析
(2)体育场(-4,2),火车站(-1,1),文化宫(0,-2)
【分析】(1)直接利用超市和市场的坐标得出原点的位置进而得出答案;
(2)利用所建立的平面直角坐标系即可得出答案.
(1)
解:如图所示:
(2)
由平面直角坐标系知,
体育场的坐标为(-4,2),火车站的坐标为(-1,1),文化宫的坐标为(0,-2).
【点睛】此题主要考查了坐标确定位置,正确得出原点位置是解题关键.
