全等三角形的复习(一)(浙江省台州市椒江区)
文档属性
| 名称 | 全等三角形的复习(一)(浙江省台州市椒江区) |  | |
| 格式 | rar | ||
| 文件大小 | 90.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-18 19:57:00 | ||
图片预览


文档简介
全等三角形复习(一)
沈小兵 2006.10
一、教学目标
1、理解五种三角形全等的判断的方法之间的关系,以及应用的条件。
2、利用全等三角形来证明相关的问题。
二、教学重点
1、从应用的角度将特殊形的主要特性系统化 , 为学生应用这些特性解题奠定基础。
2、通过对典型例题的解法的探讨,激活学生的解题思维,提高学生的解题水平。
三、教学难点
如何培养学生的逻辑思维能力
四、教学过程
1、全等三角形常见的模型
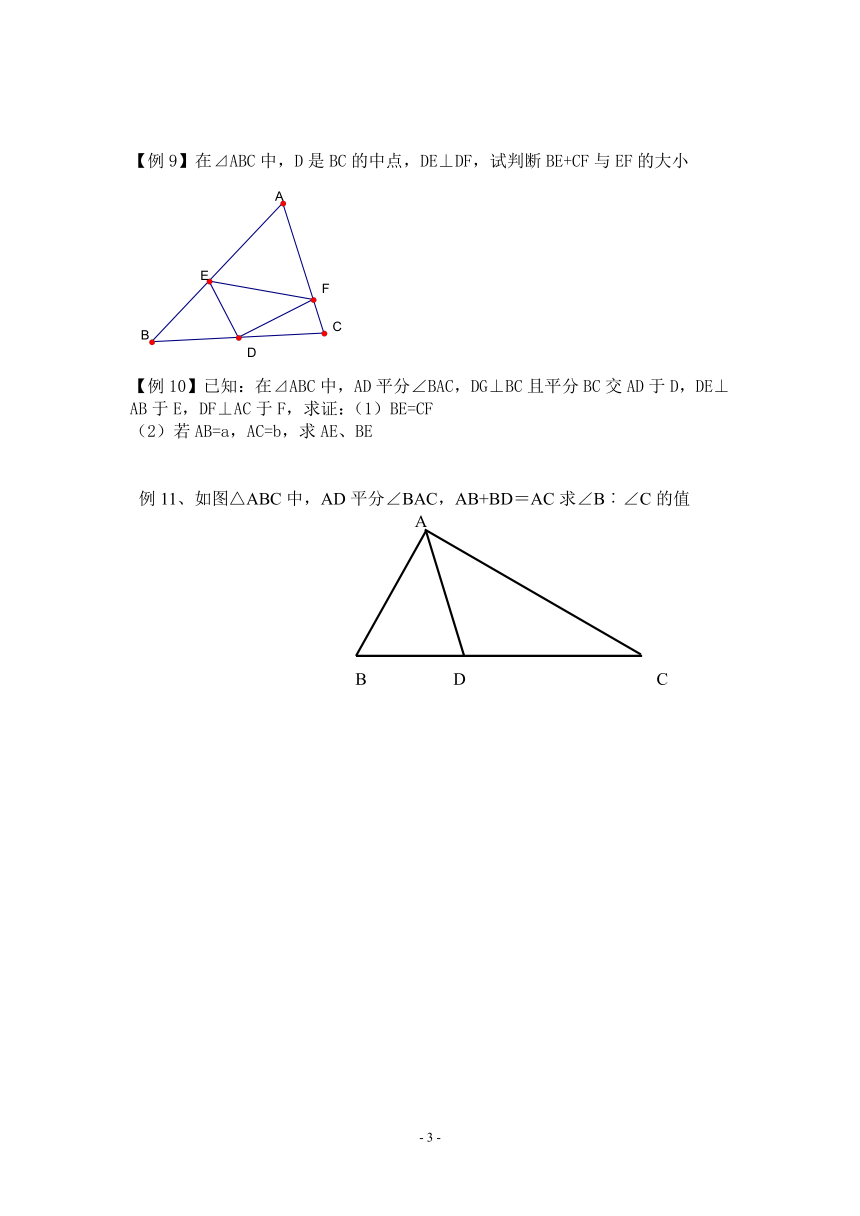
【例1】 如图,∠E=∠F=90°,∠B=∠C,AC=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN,其中正确的结论是 (把你认为所有正确结论的序号填上).
【例2】 在△ABC中,AC=5,中线AD=4,则边AB的取值范围是( )
A.1【例3】 如图,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB
求证:(1)AP=AQ;(2)AP⊥AQ.(第16届江苏省竞赛题)
【例4】 若两个三角形的两边和其中一边上的高分别对应相等,试判断这两个三角形的第三边所对的角之间的关系,并说明理由.
(第9届“五羊杯”竞赛题改编题)
【例5】 如图,已知四边形纸片ABCD中,AD∥ BC,将∠ABC、∠DAB分别对折,如果两条折痕恰好相交于DC上一点E,你能获得哪些结论
【例6】如图所示.△ABC是等腰三角形,D,E分别是腰AB及AC延长线上的一点,且BD=CE,连接DE交底BC于G.求证:GD=GE.
【例7】如图所示.∠A=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E.求证:∠AMB=∠DMC.
【例8】在⊿ABC中,∠A=100°,∠ABC=40°BD是∠ABC的平分线,延长BD到E,使DE=AD,求证:BC=AB+CE
【例9】在⊿ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小
【例10】已知:在⊿ABC中,AD平分∠BAC,DG⊥BC且平分BC交AD于D,DE⊥AB于E,DF⊥AC于F,求证:(1)BE=CF
(2)若AB=a,AC=b,求AE、BE
例11、如图△ABC中,AD平分∠BAC,AB+BD=AC求∠B︰∠C的值
A
B D C
全等三角形复习作业(1)
沈小兵 2006.10
一、选择题
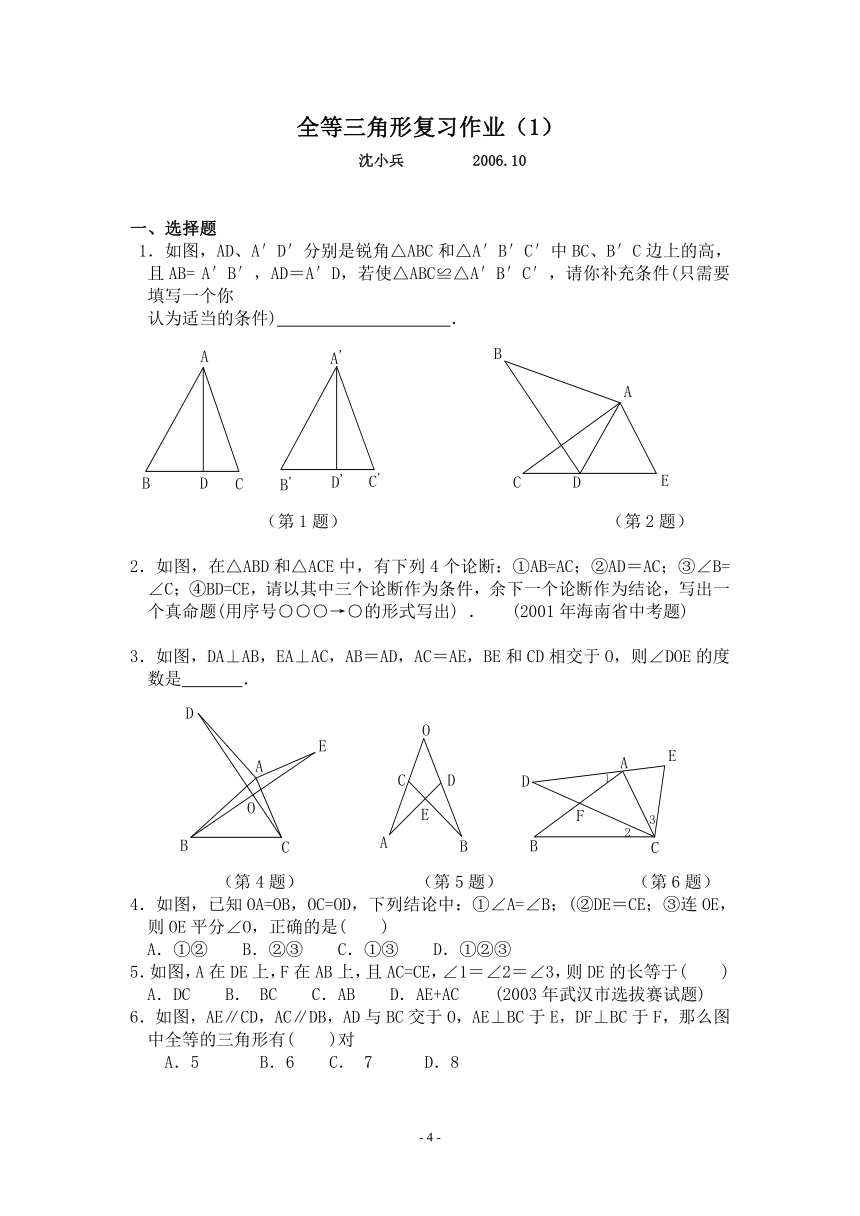
1.如图,AD、A′D′分别是锐角△ABC和△A′B′C′中BC、B′C边上的高,且AB= A′B′,AD=A′D,若使△ABC≌△A′B′C′,请你补充条件(只需要填写一个你
认为适当的条件) .
(第1题) (第2题)
2.如图,在△ABD和△ACE中,有下列4个论断:①AB=AC;②AD=AC;③∠B=∠C;④BD=CE,请以其中三个论断作为条件,余下一个论断作为结论,写出一个真命题(用序号○○○→○的形式写出) . (2001年海南省中考题)
3.如图,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,则∠DOE的度数是 .
(第4题) (第5题) (第6题)
4.如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;(②DE=CE;③连OE,则OE平分∠O,正确的是( )
A.①② B.②③ C.①③ D.①②③
5.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC B. BC C.AB D.AE+AC (2003年武汉市选拔赛试题)
6.如图,AE∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A.5 B.6 C. 7 D.8
7.审查下列各判断,其中正确的有( )个
①两条直角边对应相等的两个直角三角形全等;
②有两边和一角对应相等的两个三角形全等;
③腰长相等且有一个角是300的两个等腰三角形全等;
④腰长相等且有一个角是910的两个等腰三角形全等。
A 1 B 2 C 3 D 4
8.下列说法中,正确的是( )
A 全等三角形的角平分线长相等 B 全等三角形的中线长相等
C 全等三角形的周长相等 D 全等三角形的高相等
9.根据下列条件,能够确定两个三角形全等的是( )
A 一边及这边上的高线对应相等 B 一边及这边上的中线对应相等
C 两个角及第三个角的平分线对应相等 D 两条边及一边上的高对应相等
10.如图,已知AE=CF,D、B到AC的距离DE=BF, 则图中全等的三角形有( )对
A 1 B 2 C 3 D 4
11.如图,△ABC中,∠C=900,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为( )
A 4cm B 6cm C 10cm D 以上都不对
(第4题) (第5题) (第6题)
12.如图,∠B=∠C,BD=CE,CD=BF,则∠EDF=( )
A 900-∠A B 900-
C 1800-2∠A D 450-
13.下列命题中,不正确的是( )
A 有两角和其中一角的对边对应相等的两个等腰三角形全等
B 面积相等的两个直角三角形全等
C 有一边相等的两个等边三角形全等
D有两边和其中一边上的中线对应相等的两个三角形全等
14.下列说法正确的是( )
A 一边相等的两个直角三角形全等 B斜边相等的两个直角三角形全等
C 斜边相等的两个等腰直角三角形全等
D 斜边及斜边上的中线对应相等的两个直角三角形全等
二、填空题
1、如图,AD是△ABC的一条中线,CF⊥AD于F,BE⊥AD于E,BC=14cm,BE=6cm,则CD=_______cm,CF=_______cm。
2、如图,已知AC=AE,AB=AD,BC=DE,∠BAD=800,则∠CAE=____________。
3、如图,AC和BE互相垂直平分,D为垂足,若∠ACB=540,则∠E=________。
4、如下左图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=380,那么∠BED=______。
5、如上右图,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,则BE和DC的关系是__________________。
(第6题) (第7题)
6.如图,把△ABC绕点C顺时针旋转35°,得到△A′B′C′,A′B′交AC于点D,已知∠A′DC=90°,求∠A的度数. (2001年贵州省中考题)
7.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC= .
8.如图,在△ABE和△ACD中,给出以下4个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中3个论断为题设,填人下面的“已知”栏中,一个论断为结论,填人下面的“求证”栏中,使之组成一个真命题,并写出证明过程.
已知:
求证:
9.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)大小关系是( )
A.m+n> b+c B. m+n(第11题) (第12题)
10.如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且AE=(AB+AD),求∠ABC+∠ADC的度数. (上海市竞赛题)
11、如图,∠D=∠E,DN=EM,CN=AM,求证:点B是线段AC的中点。
12、已知,如上右图,∠BAC=∠BCA,BD=CD,CE=AB,求证:AE=2AD。
13、如图,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:。
14、如上右图,已知△ABC是等边三角形,E是AC延长线上的任意一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,求证:△CMN是等边三角形。
- 7 -
沈小兵 2006.10
一、教学目标
1、理解五种三角形全等的判断的方法之间的关系,以及应用的条件。
2、利用全等三角形来证明相关的问题。
二、教学重点
1、从应用的角度将特殊形的主要特性系统化 , 为学生应用这些特性解题奠定基础。
2、通过对典型例题的解法的探讨,激活学生的解题思维,提高学生的解题水平。
三、教学难点
如何培养学生的逻辑思维能力
四、教学过程
1、全等三角形常见的模型
【例1】 如图,∠E=∠F=90°,∠B=∠C,AC=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN,其中正确的结论是 (把你认为所有正确结论的序号填上).
【例2】 在△ABC中,AC=5,中线AD=4,则边AB的取值范围是( )
A.1
求证:(1)AP=AQ;(2)AP⊥AQ.(第16届江苏省竞赛题)
【例4】 若两个三角形的两边和其中一边上的高分别对应相等,试判断这两个三角形的第三边所对的角之间的关系,并说明理由.
(第9届“五羊杯”竞赛题改编题)
【例5】 如图,已知四边形纸片ABCD中,AD∥ BC,将∠ABC、∠DAB分别对折,如果两条折痕恰好相交于DC上一点E,你能获得哪些结论
【例6】如图所示.△ABC是等腰三角形,D,E分别是腰AB及AC延长线上的一点,且BD=CE,连接DE交底BC于G.求证:GD=GE.
【例7】如图所示.∠A=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E.求证:∠AMB=∠DMC.
【例8】在⊿ABC中,∠A=100°,∠ABC=40°BD是∠ABC的平分线,延长BD到E,使DE=AD,求证:BC=AB+CE
【例9】在⊿ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小
【例10】已知:在⊿ABC中,AD平分∠BAC,DG⊥BC且平分BC交AD于D,DE⊥AB于E,DF⊥AC于F,求证:(1)BE=CF
(2)若AB=a,AC=b,求AE、BE
例11、如图△ABC中,AD平分∠BAC,AB+BD=AC求∠B︰∠C的值
A
B D C
全等三角形复习作业(1)
沈小兵 2006.10
一、选择题
1.如图,AD、A′D′分别是锐角△ABC和△A′B′C′中BC、B′C边上的高,且AB= A′B′,AD=A′D,若使△ABC≌△A′B′C′,请你补充条件(只需要填写一个你
认为适当的条件) .
(第1题) (第2题)
2.如图,在△ABD和△ACE中,有下列4个论断:①AB=AC;②AD=AC;③∠B=∠C;④BD=CE,请以其中三个论断作为条件,余下一个论断作为结论,写出一个真命题(用序号○○○→○的形式写出) . (2001年海南省中考题)
3.如图,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,则∠DOE的度数是 .
(第4题) (第5题) (第6题)
4.如图,已知OA=OB,OC=OD,下列结论中:①∠A=∠B;(②DE=CE;③连OE,则OE平分∠O,正确的是( )
A.①② B.②③ C.①③ D.①②③
5.如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于( )
A.DC B. BC C.AB D.AE+AC (2003年武汉市选拔赛试题)
6.如图,AE∥CD,AC∥DB,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )对
A.5 B.6 C. 7 D.8
7.审查下列各判断,其中正确的有( )个
①两条直角边对应相等的两个直角三角形全等;
②有两边和一角对应相等的两个三角形全等;
③腰长相等且有一个角是300的两个等腰三角形全等;
④腰长相等且有一个角是910的两个等腰三角形全等。
A 1 B 2 C 3 D 4
8.下列说法中,正确的是( )
A 全等三角形的角平分线长相等 B 全等三角形的中线长相等
C 全等三角形的周长相等 D 全等三角形的高相等
9.根据下列条件,能够确定两个三角形全等的是( )
A 一边及这边上的高线对应相等 B 一边及这边上的中线对应相等
C 两个角及第三个角的平分线对应相等 D 两条边及一边上的高对应相等
10.如图,已知AE=CF,D、B到AC的距离DE=BF, 则图中全等的三角形有( )对
A 1 B 2 C 3 D 4
11.如图,△ABC中,∠C=900,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为( )
A 4cm B 6cm C 10cm D 以上都不对
(第4题) (第5题) (第6题)
12.如图,∠B=∠C,BD=CE,CD=BF,则∠EDF=( )
A 900-∠A B 900-
C 1800-2∠A D 450-
13.下列命题中,不正确的是( )
A 有两角和其中一角的对边对应相等的两个等腰三角形全等
B 面积相等的两个直角三角形全等
C 有一边相等的两个等边三角形全等
D有两边和其中一边上的中线对应相等的两个三角形全等
14.下列说法正确的是( )
A 一边相等的两个直角三角形全等 B斜边相等的两个直角三角形全等
C 斜边相等的两个等腰直角三角形全等
D 斜边及斜边上的中线对应相等的两个直角三角形全等
二、填空题
1、如图,AD是△ABC的一条中线,CF⊥AD于F,BE⊥AD于E,BC=14cm,BE=6cm,则CD=_______cm,CF=_______cm。
2、如图,已知AC=AE,AB=AD,BC=DE,∠BAD=800,则∠CAE=____________。
3、如图,AC和BE互相垂直平分,D为垂足,若∠ACB=540,则∠E=________。
4、如下左图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=380,那么∠BED=______。
5、如上右图,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,则BE和DC的关系是__________________。
(第6题) (第7题)
6.如图,把△ABC绕点C顺时针旋转35°,得到△A′B′C′,A′B′交AC于点D,已知∠A′DC=90°,求∠A的度数. (2001年贵州省中考题)
7.在△ABC中,高AD和BE交于H点,且BH=AC,则∠ABC= .
8.如图,在△ABE和△ACD中,给出以下4个论断:①AB=AC;②AD=AE;③AM=AN;④AD⊥DC,AE⊥BE.以其中3个论断为题设,填人下面的“已知”栏中,一个论断为结论,填人下面的“求证”栏中,使之组成一个真命题,并写出证明过程.
已知:
求证:
9.如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)大小关系是( )
A.m+n> b+c B. m+n
10.如图,在四边形ABCD中,AC平分∠BAD,过C作CE⊥AB于E,并且AE=(AB+AD),求∠ABC+∠ADC的度数. (上海市竞赛题)
11、如图,∠D=∠E,DN=EM,CN=AM,求证:点B是线段AC的中点。
12、已知,如上右图,∠BAC=∠BCA,BD=CD,CE=AB,求证:AE=2AD。
13、如图,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:。
14、如上右图,已知△ABC是等边三角形,E是AC延长线上的任意一点,选择一点D,使得△CDE是等边三角形,如果M是线段AD的中点,N是线段BE的中点,求证:△CMN是等边三角形。
- 7 -
