23.2.1中心对称(36张幻灯片)
文档属性
| 名称 | 23.2.1中心对称(36张幻灯片) |
|
|
| 格式 | zip | ||
| 文件大小 | 571.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-17 08:49:05 | ||
图片预览



文档简介
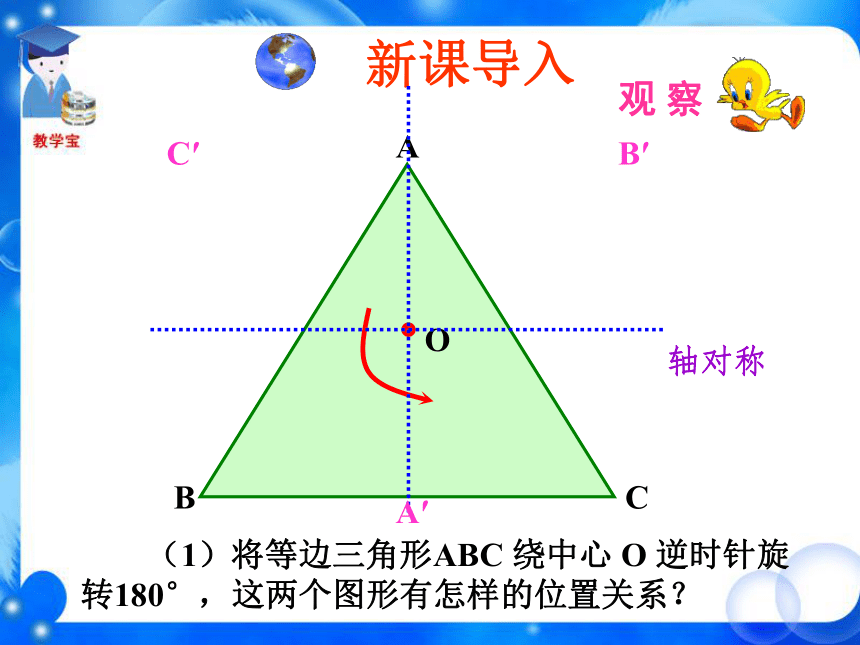
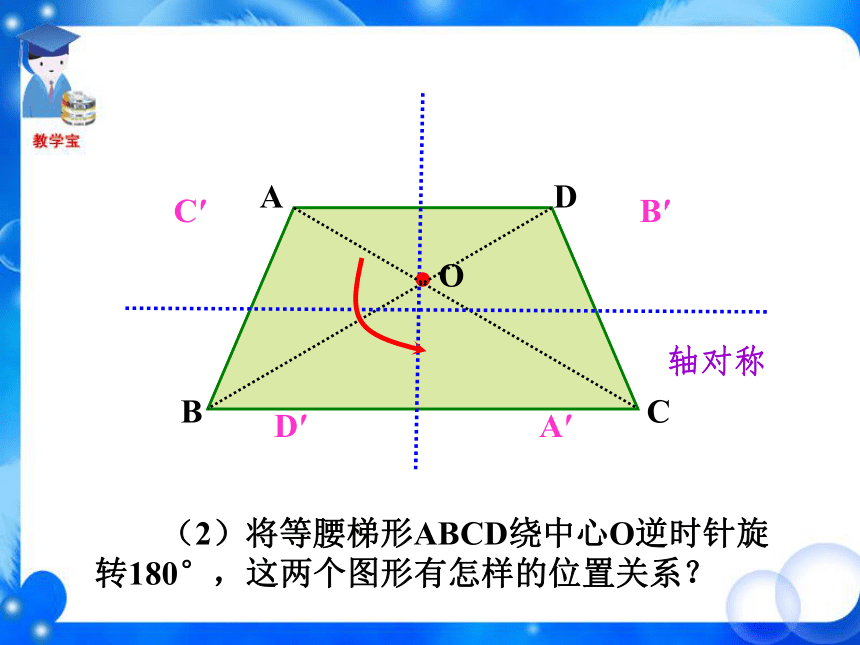
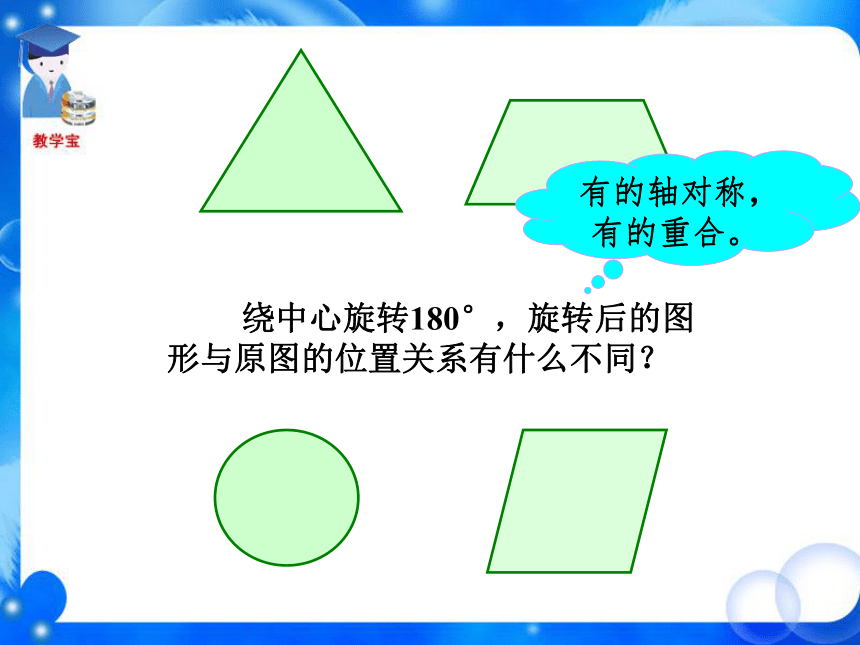
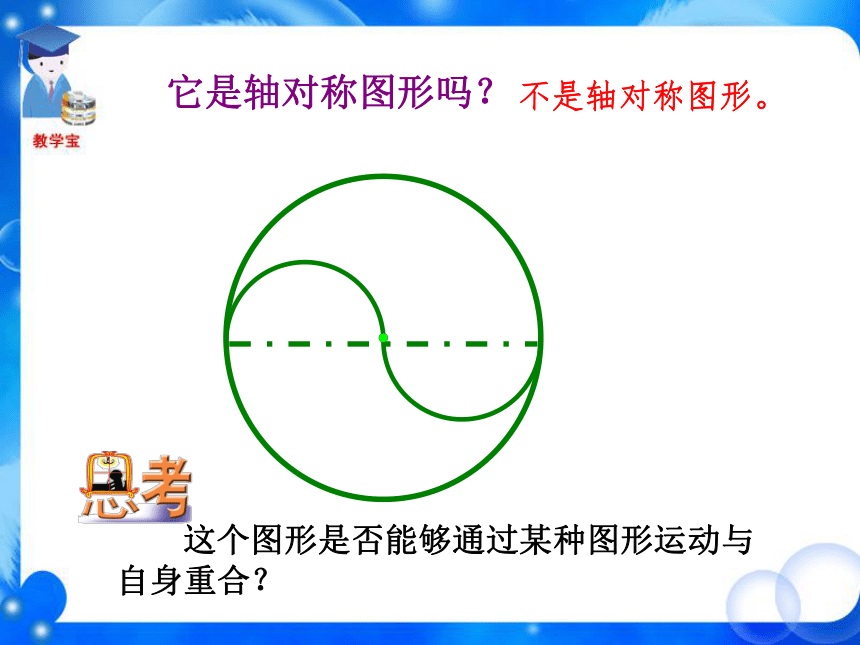
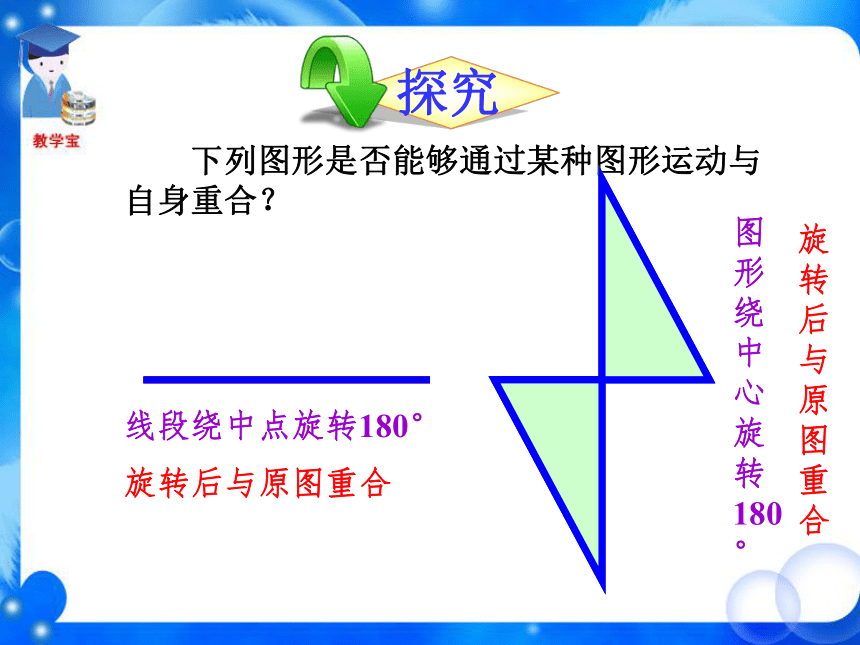
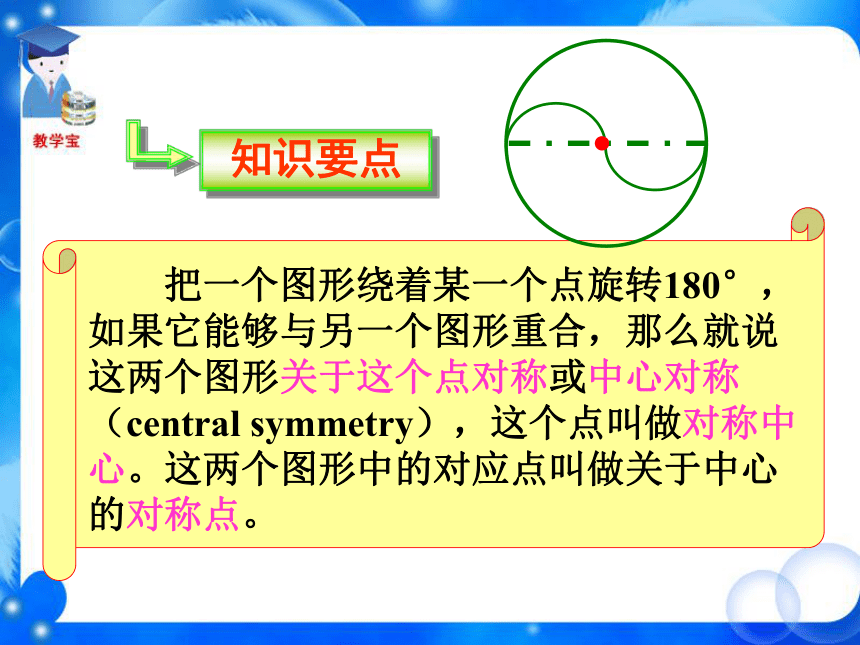
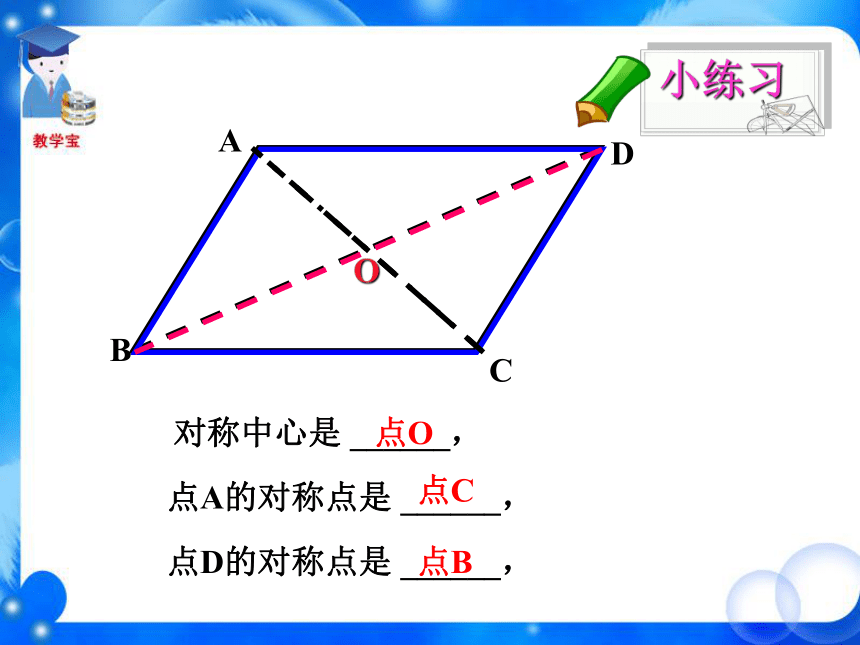
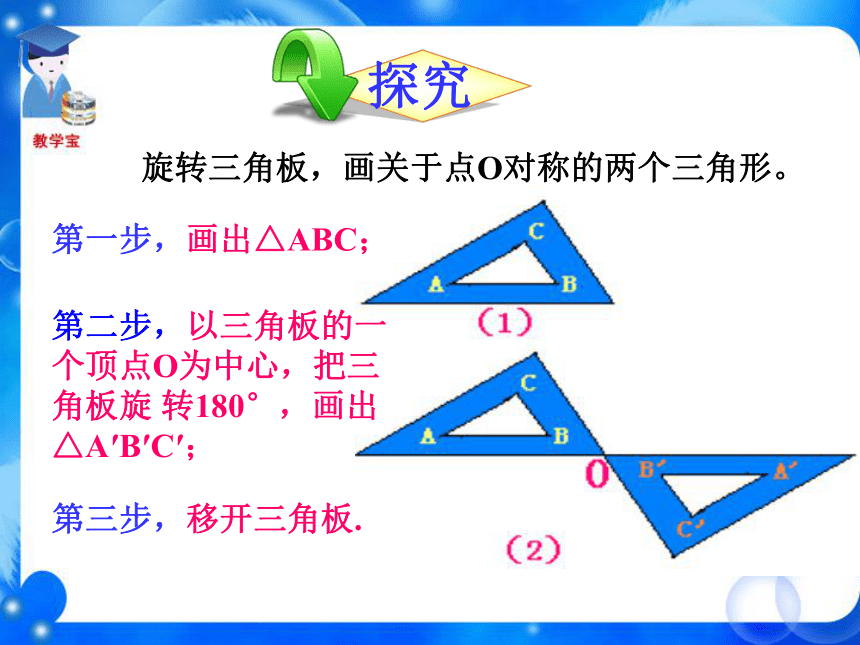
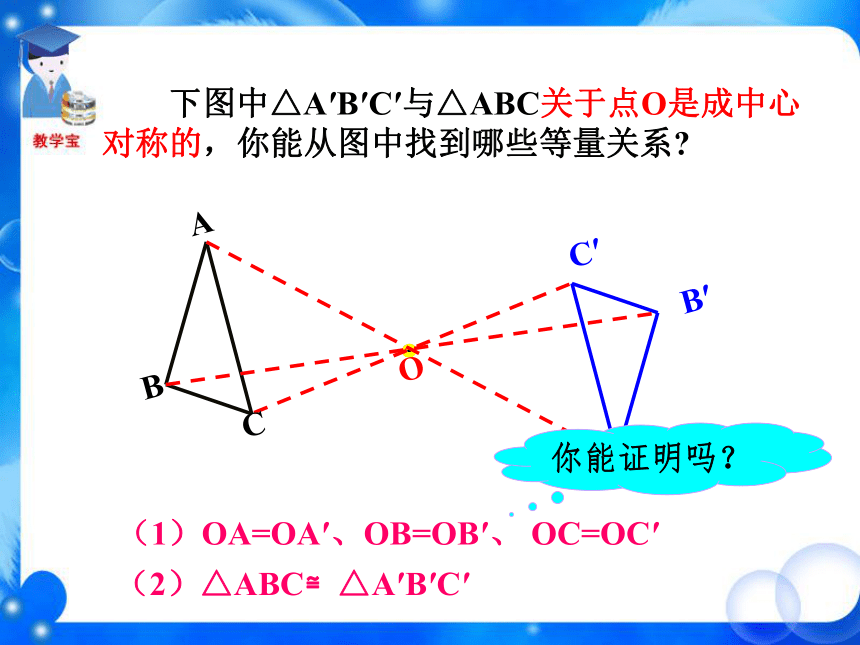
课件36张PPT。 (1)将等边三角形ABC 绕中心 O 逆时针旋转180°,这两个图形有怎样的位置关系? 新课导入观 察ABCOB′C′轴对称A′ (2)将等腰梯形ABCD绕中心O逆时针旋转180°,这两个图形有怎样的位置关系?ADBCOA′B′C′D′轴对称 (3)将圆O 绕圆心 O 顺时针旋转180°,这两个图形有怎样的位置关系?O重合 (4)将平行四边形ABCD绕中心O逆时针旋转180°,这两个图形有怎样的位置关系?ABCDOA′B′C′D′重合 绕中心旋转180°,旋转后的图形与原图的位置关系有什么不同? 有的轴对称,有的重合。它是轴对称图形吗? 这个图形是否能够通过某种图形运动与自身重合? 不是轴对称图形。 下列图形是否能够通过某种图形运动与自身重合? 线段绕中点旋转180°旋转后与原图重合图形绕中心旋转180°旋转后与原图重合 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称(central symmetry),这个点叫做对称中心。这两个图形中的对应点叫做关于中心的对称点。OBACD对称中心是 ______,点O点A的对称点是 ______,点D的对称点是 ______,点C点B小练习旋转三角板,画关于点O对称的两个三角形。第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋 转180°,画出△A′B′C′;第三步,移开三角板. 下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?A′B′C′ABCO (1)OA=OA′、OB=OB′、 OC=OC′(2)△ABC≌△A′B′C′你能证明吗?证明:(1)点A′是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA=OA′,
即点O是线段AA′的中点。
同理,点O也在线段BB′和CC′上,
且OB=OB′,OC=OC′,
即点O是BB′和CC′的中点。 求证:(1)OA=OA′、OB=OB′、 OC=OC′证明:(1)在△ABC和△A′B′C′中,OA=OA′,OB=OB′,∠AOB=∠A′OB′
∴△AOB≌△A′OB′
∴AB=A′B′
同理:AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′求证:(2)△ABC≌△A′B′C′ 1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
2.关于中心对称的两个图形是全等图形。 点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗? 对称中心平分连结两个对称点的线段.EF经过点O,分别交AB、CD于E、F。解:∵平行四边形是中心对称图形,O是对称中心.∴点E、F是关于点O的对称点。
∴OE=OF。 3. 以点O为对称中心,画出与△ABC关于点O对称的△A′B′C′。A′C′B′△A′B′C′即为所求的三角形。三角形的中心对称三角形的作法 4. 画四边形A′B′C′D′,使它与已知四边形关于O点对称。ABA′C′B′D′DOC四边形A′B′C′D′即为所求的图形。四边形的中心对称四边形的作法 5. 画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。EFGMNA′B′C′ 6. 画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称。△A′B′C′即为所求的三角形。 1. 中心对称与轴对称的区别和联系? 课堂小结有一条对称轴——直线图形沿对称轴对折(翻折180°)后重合对称点的连线被对称轴垂直平分有一个对称中心——点图形绕对称中心旋转180°后重合对称点连线经过对称中心,且被对称中心平分 2. 中心对称的两条基本性质:
(1)关于中心对称的两个图形,对应点所连线都经过对称中心,而且被对称中心所平分。
(2)关于中心对称的两个图形是全等图形及其它们的应用。 1. △ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法。 作法:
(1)连结OA、OB、OC、
OD;
(2)分别以OB、OB为边作
∠BOM=∠CON=∠AOD; (3)分别截取OE=OB,
OF=OC;
(4)依次连结DE、EF、FD;
即:△DEF就是所求作的三角
形,如图所示。 随堂练习 2. 四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答。
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由。
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点。解:作法:
(1)延长AD,并且使得DA′=AD
(2)同理:BD=B′D,CD=C′D
(3)连结A′B′、B′C′、C′D,则四边形A′B′C′D为所求的四边形,如图所示。 答:(1)根据中心对称的定义便知这两个图形是中心对称图形,对称中心是D点。(2)A、B、C、D关于中心D的对称点是A′、B′、C′、D′,这里的D′与D重合。 3. 已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形。 解:(1)延长AD,且使AD=DA′,因为C点关于D的中心对称点是B(C′),B点关于中心D的对称点为C(B′)
(2)连结A′B′、A′C′。
则△A′B′C′为所求作的三角形,如图所示。 4. 已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称。解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示。
(2)同样画出点B和点C的对称点E和F。
(3)顺次连结DE、EF、FD。
则△DEF即为所求的三角形。 5. 已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法) 6. 在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置。
(1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积。
(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式。 解:(1)∵CC′=3,CB= 4且 AC=BC
∴BC′=C′D=1
∴S△BDC′= ×1×1=
(2)∵CC′= x,∴BC′= 4-x
∵AC=BC=4
∴DC′=4-x
∴S△BDC′= (4-x)(4-x)= 7. 等边△ABC内有一点O,说明:OA+OB>OC。解:如图,把△AOC以A为旋转中心顺时针方向旋转60°后,到△AO′B的位置,则△AOC≌△AO′B。∴AO=AO′,OC=O′B 又∵∠OAO′=60°,∴△AO′O为等边三角形.
∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC 8. 矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长。解:连接AF,
∵点C与点A重合,折痕为EF,即EF垂直平分AC。
∴AF=CF,AO=CO,∠FOC=90°,又四边形ABCD为矩形,∠B=90°,AB=CD=3,AD=BC=4
设CF=x,则AF=x,BF=4-x,
由勾股定理,得
∴AC=5,
∵
∴
∴
∵∠FOC=90°
∴
同理 ,即
即点O是线段AA′的中点。
同理,点O也在线段BB′和CC′上,
且OB=OB′,OC=OC′,
即点O是BB′和CC′的中点。 求证:(1)OA=OA′、OB=OB′、 OC=OC′证明:(1)在△ABC和△A′B′C′中,OA=OA′,OB=OB′,∠AOB=∠A′OB′
∴△AOB≌△A′OB′
∴AB=A′B′
同理:AC=A′C′,BC=B′C′
∴△ABC≌△A′B′C′求证:(2)△ABC≌△A′B′C′ 1.关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分。
2.关于中心对称的两个图形是全等图形。 点O是平行四边形的对称中心,点A、C关于点O对称,有AO=CO,那么OE=OF吗? 对称中心平分连结两个对称点的线段.EF经过点O,分别交AB、CD于E、F。解:∵平行四边形是中心对称图形,O是对称中心.∴点E、F是关于点O的对称点。
∴OE=OF。 3. 以点O为对称中心,画出与△ABC关于点O对称的△A′B′C′。A′C′B′△A′B′C′即为所求的三角形。三角形的中心对称三角形的作法 4. 画四边形A′B′C′D′,使它与已知四边形关于O点对称。ABA′C′B′D′DOC四边形A′B′C′D′即为所求的图形。四边形的中心对称四边形的作法 5. 画一个与已知四边形ABCD中心对称图形。
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心。EFGMNA′B′C′ 6. 画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称。△A′B′C′即为所求的三角形。 1. 中心对称与轴对称的区别和联系? 课堂小结有一条对称轴——直线图形沿对称轴对折(翻折180°)后重合对称点的连线被对称轴垂直平分有一个对称中心——点图形绕对称中心旋转180°后重合对称点连线经过对称中心,且被对称中心平分 2. 中心对称的两条基本性质:
(1)关于中心对称的两个图形,对应点所连线都经过对称中心,而且被对称中心所平分。
(2)关于中心对称的两个图形是全等图形及其它们的应用。 1. △ABC绕点O旋转,使点A旋转到点D处,画出旋转后的三角形,并写出简要作法。 作法:
(1)连结OA、OB、OC、
OD;
(2)分别以OB、OB为边作
∠BOM=∠CON=∠AOD; (3)分别截取OE=OB,
OF=OC;
(4)依次连结DE、EF、FD;
即:△DEF就是所求作的三角
形,如图所示。 随堂练习 2. 四边形ABCD绕D点旋转180°,请作出旋转后的图案,写出作法并回答。
(1)这两个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由。
(2)如果是中心对称,那么A、B、C、D关于中心的对称点是哪些点。解:作法:
(1)延长AD,并且使得DA′=AD
(2)同理:BD=B′D,CD=C′D
(3)连结A′B′、B′C′、C′D,则四边形A′B′C′D为所求的四边形,如图所示。 答:(1)根据中心对称的定义便知这两个图形是中心对称图形,对称中心是D点。(2)A、B、C、D关于中心D的对称点是A′、B′、C′、D′,这里的D′与D重合。 3. 已知AD是△ABC的中线,画出以点D为对称中心,与△ABD成中心对称的三角形。 解:(1)延长AD,且使AD=DA′,因为C点关于D的中心对称点是B(C′),B点关于中心D的对称点为C(B′)
(2)连结A′B′、A′C′。
则△A′B′C′为所求作的三角形,如图所示。 4. 已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称。解:(1)连结AO并延长AO到D,使OD=OA,于是得到点A的对称点D,如图所示。
(2)同样画出点B和点C的对称点E和F。
(3)顺次连结DE、EF、FD。
则△DEF即为所求的三角形。 5. 已知四边形ABCD和点O,画四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于点O成中心对称(只保留作图痕迹,不要求写出作法) 6. 在△ABC中,∠C=70°,BC=4,AC=4,现将△ABC沿CB方向平移到△A′B′C′的位置。
(1)若平移的距离为3,求△ABC与△A′B′C′重叠部分的面积。
(2)若平移的距离为x(0≤x≤4),求△ABC与△A′B′C′重叠部分的面积y,写出y与x的关系式。 解:(1)∵CC′=3,CB= 4且 AC=BC
∴BC′=C′D=1
∴S△BDC′= ×1×1=
(2)∵CC′= x,∴BC′= 4-x
∵AC=BC=4
∴DC′=4-x
∴S△BDC′= (4-x)(4-x)= 7. 等边△ABC内有一点O,说明:OA+OB>OC。解:如图,把△AOC以A为旋转中心顺时针方向旋转60°后,到△AO′B的位置,则△AOC≌△AO′B。∴AO=AO′,OC=O′B 又∵∠OAO′=60°,∴△AO′O为等边三角形.
∴AO=OO′
在△BOO′中,OO′+OB>BO′
即OA+OB>OC 8. 矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长。解:连接AF,
∵点C与点A重合,折痕为EF,即EF垂直平分AC。
∴AF=CF,AO=CO,∠FOC=90°,又四边形ABCD为矩形,∠B=90°,AB=CD=3,AD=BC=4
设CF=x,则AF=x,BF=4-x,
由勾股定理,得
∴AC=5,
∵
∴
∴
∵∠FOC=90°
∴
同理 ,即
同课章节目录
