13.3.1 圆的初步认识(第一课时)课件
文档属性
| 名称 | 13.3.1 圆的初步认识(第一课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 320.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-06-17 21:25:28 | ||
图片预览






文档简介
课件20张PPT。第一课时
圆的基本概念
§13.3.1 圆的初步认识教学目标1.经历从现实世界中抽象出圆的过程,发展
学生的数学建模意识。
2.能从圆的生成和 集合的两个不同的角度
去认识圆的概念,经历探索点于圆的位置
关系的过程。
3.理解弦、弧、半圆、等圆、同心圆、等弧
的概念。
教学重难点重点:圆的定义及有关概念
难点:从集合的观点定义圆
圆是生活中常见的图形,许多物体都给我们以圆的形象问题:为什么自古到今从古代的
马车到现在的自行车他们的轮
子都做成圆的,而不做成方形了
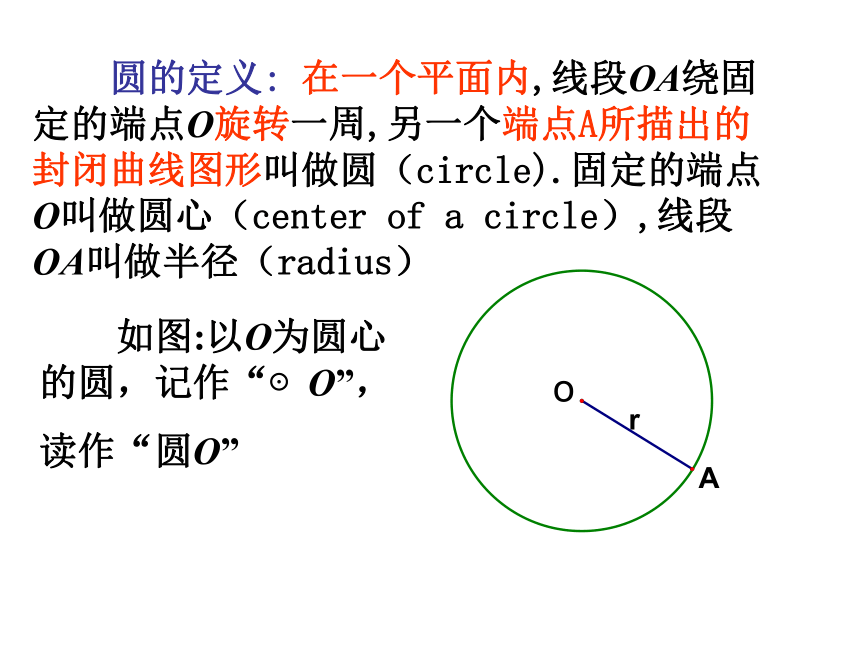
或三角形了 ?自行车让大风车转起来大风车. 圆的定义: 在一个平面内,线段OA绕固定的端点O旋转一周,另一个端点A所描出的封闭曲线图形叫做圆(circle).固定的端点O叫做圆心(center of a circle),线段OA叫做半径(radius) 如图:以O为圆心的圆,记作“⊙O”,
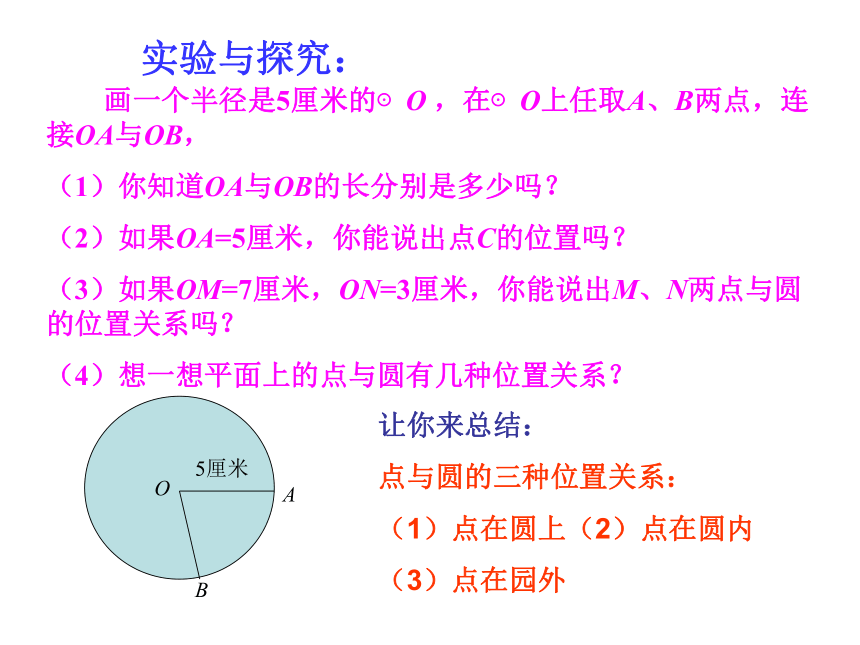
读作“圆O”实验与探究: 画一个半径是5厘米的⊙O ,在⊙O上任取A、B两点,连接OA与OB,
(1)你知道OA与OB的长分别是多少吗?
(2)如果OA=5厘米,你能说出点C的位置吗?
(3)如果OM=7厘米,ON=3厘米,你能说出M、N两点与圆的位置关系吗?
(4)想一想平面上的点与圆有几种位置关系?OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上(2)点在圆内
(3)点在园外由圆的定义可知:
(1) 圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上因此,圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等于定长r的点的集合.请你用集合的语言描述下面的两个概念:
(1)圆的内部是 点的集合.
(2)圆的外部是 点的集合.题组(一)要点追踪,相信你能行1.已知⊙O的半径为3,A为线段PO的中点,则当OP=6
时,点A与⊙O的 位置关系( ).
A.点在圆内 B.点在圆上
C.点在圆外 D.不能确定
2.正方形ABCD的边长为2,以A为圆心,1为半径作
⊙A,则点B在⊙A ;点C在 ⊙A ;
点D在 ⊙A .
3.已知点O为圆心,已知线段a为半径,可以做 个
圆.试想一下,如果车轮不是圆的(比如椭圆或正方形的),坐车的人会是什么感觉?知识链接生活点A是圆上的点OA是圆的半径 连接圆上任意两点的线段(如图中的线段BC、BD)叫做弦(chord) 经过圆心的弦(如图中的BD)叫做直径(diameter)COBACOBA小于半圆的弧叫做劣弧.如AB大于半圆的弧叫做优弧(用三个点表示)如BCA弧的分类: (1)优弧(大于半圆的弧)
(2)半圆弧(等于半圆的弧)
(3)劣弧(小于半圆的弧)︵︵扇形扇形:一条弧和经过这条弧的两个端点的两
条半径所组成的图形叫做扇形。
如图中的两个扇形是有半径OA及OB分
别与AmB和AnB所组成的扇
思考?
圆中的两条半径可把圆
分成几个扇形?
mnOBA︵︵题组(二)看谁分辨的快,考考你:
1.下列命题正确的是( )
A .面积相等的两个圆是等圆B.过圆心的线段叫做圆的直径
C.大于劣弧的弧叫做优弧
D.圆内任意一点到圆上任意一点的距离都小于半径
2.如图,在⊙O中,AB是⊙O的直径,P为OB上一点(不同于
O、B),CD、EF是 ⊙O中过点P的两条弦,图中有
条弦,以A为一端点的劣弧有 条.
快速检测1.下列说法正确的是( )
A.直径不是圆的弦 B.半圆周不是弧
C.等于半径两倍的弦断叫 D.过园内一点可以做无数条弦
2.在同一圆中,劣弧比半圆周 ,优弧比半圆周 ,
同圆或等圆的半径长 .
3.解答题(能力提升,拓展思维)
如图, ⊙M的半径r=3cm,⊙M与
直角坐标系中的x轴、y轴分别交于
A、B两点,求A、B、C、D各点的
坐标.
1.这节课我们学习了什么知
识,我们有什么新的感受?
2.把你的疑问说出来,大家来
帮忙.课堂小结作业:1.必做题:课本P152 习题13.3 第1、2、3题2.选做题
如图,已知A、B两点的距离是5cm,再图上标出:
(1)到点A 的距离是4厘米,且到点B的距离是3厘
米的点;
(2)到点A 的距离小于4厘米,且到点B的距离小
于3厘米的点;
AB谁游戏人生,他将一事无成!东平腊山栈桥
圆的基本概念
§13.3.1 圆的初步认识教学目标1.经历从现实世界中抽象出圆的过程,发展
学生的数学建模意识。
2.能从圆的生成和 集合的两个不同的角度
去认识圆的概念,经历探索点于圆的位置
关系的过程。
3.理解弦、弧、半圆、等圆、同心圆、等弧
的概念。
教学重难点重点:圆的定义及有关概念
难点:从集合的观点定义圆
圆是生活中常见的图形,许多物体都给我们以圆的形象问题:为什么自古到今从古代的
马车到现在的自行车他们的轮
子都做成圆的,而不做成方形了
或三角形了 ?自行车让大风车转起来大风车. 圆的定义: 在一个平面内,线段OA绕固定的端点O旋转一周,另一个端点A所描出的封闭曲线图形叫做圆(circle).固定的端点O叫做圆心(center of a circle),线段OA叫做半径(radius) 如图:以O为圆心的圆,记作“⊙O”,
读作“圆O”实验与探究: 画一个半径是5厘米的⊙O ,在⊙O上任取A、B两点,连接OA与OB,
(1)你知道OA与OB的长分别是多少吗?
(2)如果OA=5厘米,你能说出点C的位置吗?
(3)如果OM=7厘米,ON=3厘米,你能说出M、N两点与圆的位置关系吗?
(4)想一想平面上的点与圆有几种位置关系?OAB5厘米让你来总结:
点与圆的三种位置关系:
(1)点在圆上(2)点在圆内
(3)点在园外由圆的定义可知:
(1) 圆上的各点到定点(圆心O)的距离等于定长(半径的长r );
(2)到定点的距离等于定长的点都在圆上因此,圆心为O、半径为r的圆可以看成是平面内所有到定点O的距离等于定长r的点的集合.请你用集合的语言描述下面的两个概念:
(1)圆的内部是 点的集合.
(2)圆的外部是 点的集合.题组(一)要点追踪,相信你能行1.已知⊙O的半径为3,A为线段PO的中点,则当OP=6
时,点A与⊙O的 位置关系( ).
A.点在圆内 B.点在圆上
C.点在圆外 D.不能确定
2.正方形ABCD的边长为2,以A为圆心,1为半径作
⊙A,则点B在⊙A ;点C在 ⊙A ;
点D在 ⊙A .
3.已知点O为圆心,已知线段a为半径,可以做 个
圆.试想一下,如果车轮不是圆的(比如椭圆或正方形的),坐车的人会是什么感觉?知识链接生活点A是圆上的点OA是圆的半径 连接圆上任意两点的线段(如图中的线段BC、BD)叫做弦(chord) 经过圆心的弦(如图中的BD)叫做直径(diameter)COBACOBA小于半圆的弧叫做劣弧.如AB大于半圆的弧叫做优弧(用三个点表示)如BCA弧的分类: (1)优弧(大于半圆的弧)
(2)半圆弧(等于半圆的弧)
(3)劣弧(小于半圆的弧)︵︵扇形扇形:一条弧和经过这条弧的两个端点的两
条半径所组成的图形叫做扇形。
如图中的两个扇形是有半径OA及OB分
别与AmB和AnB所组成的扇
思考?
圆中的两条半径可把圆
分成几个扇形?
mnOBA︵︵题组(二)看谁分辨的快,考考你:
1.下列命题正确的是( )
A .面积相等的两个圆是等圆B.过圆心的线段叫做圆的直径
C.大于劣弧的弧叫做优弧
D.圆内任意一点到圆上任意一点的距离都小于半径
2.如图,在⊙O中,AB是⊙O的直径,P为OB上一点(不同于
O、B),CD、EF是 ⊙O中过点P的两条弦,图中有
条弦,以A为一端点的劣弧有 条.
快速检测1.下列说法正确的是( )
A.直径不是圆的弦 B.半圆周不是弧
C.等于半径两倍的弦断叫 D.过园内一点可以做无数条弦
2.在同一圆中,劣弧比半圆周 ,优弧比半圆周 ,
同圆或等圆的半径长 .
3.解答题(能力提升,拓展思维)
如图, ⊙M的半径r=3cm,⊙M与
直角坐标系中的x轴、y轴分别交于
A、B两点,求A、B、C、D各点的
坐标.
1.这节课我们学习了什么知
识,我们有什么新的感受?
2.把你的疑问说出来,大家来
帮忙.课堂小结作业:1.必做题:课本P152 习题13.3 第1、2、3题2.选做题
如图,已知A、B两点的距离是5cm,再图上标出:
(1)到点A 的距离是4厘米,且到点B的距离是3厘
米的点;
(2)到点A 的距离小于4厘米,且到点B的距离小
于3厘米的点;
AB谁游戏人生,他将一事无成!东平腊山栈桥
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
