第19章 一次函数复习 第1课时 课件(21张PPT)
文档属性
| 名称 | 第19章 一次函数复习 第1课时 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 911.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
知识结构与要点
一次函数 章节复习
| 第1课时|
内容提要
知识结构
知识要点
针对练习
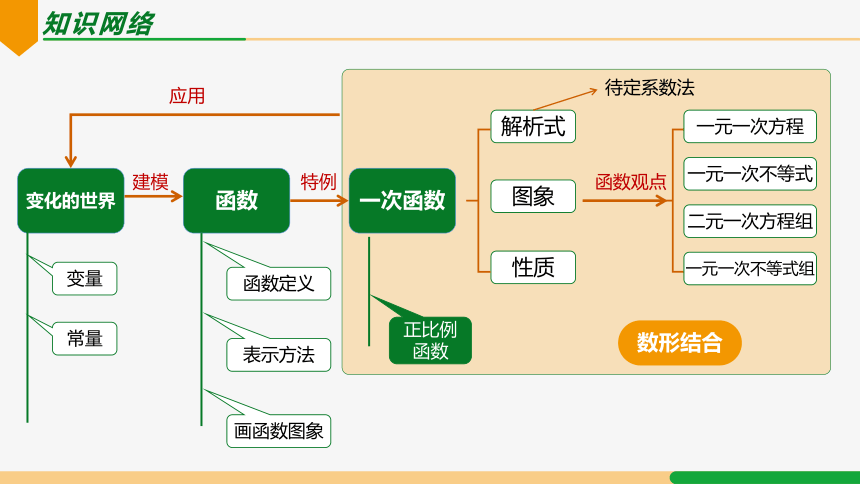
知识网络
函数
变化的世界
一次函数
性质
图象
解析式
变量
常量
建模
特例
待定系数法
函数定义
表示方法
画函数图象
正比例函数
一元一次方程
一元一次不等式
二元一次方程组
一元一次不等式组
函数观点
应用
数形结合
知识要点
一、函数
1. 常量与变量
数值发生变化的量叫变量,
数值始终不变的量叫常量.
在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
2. 函数定义:
3. 函数的图象
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法解析式法图象法
5. 函数的三种表示方法:
4. 描点法画图象的步骤:
列表、描点、连线
二、一次函数
1.一次函数与正比例函数的定义
一般地,如果 y= k x+b (k、b是常数,k ≠ 0 ),那么 y 叫做 x 的一次函数
当 b=____时,一次函数y=k x+b 变为 y= k x(k为常数, k ≠ 0),这时 y 叫做 x 的正比例函数
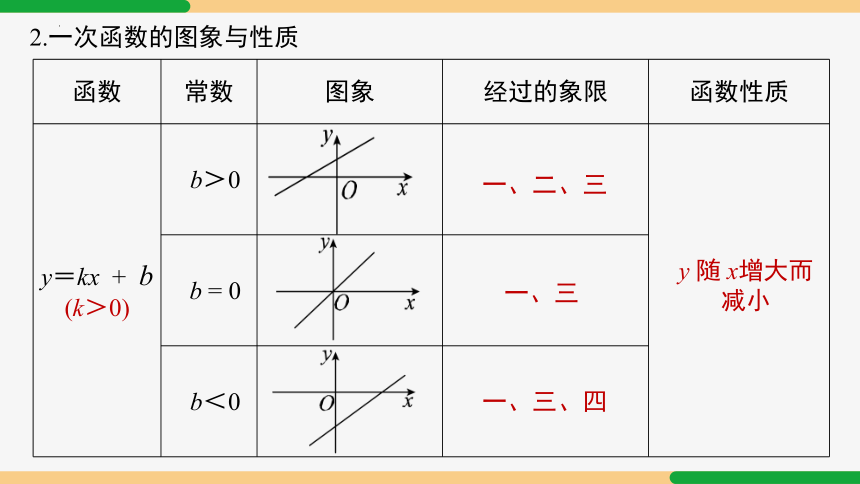
2.一次函数的图象与性质
函数 常数 图象 经过的象限 函数性质
y=kx + b (k>0) b>0
b = 0 b<0 y 随 x增大而
减小
一、三
一、二、三
一、三、四
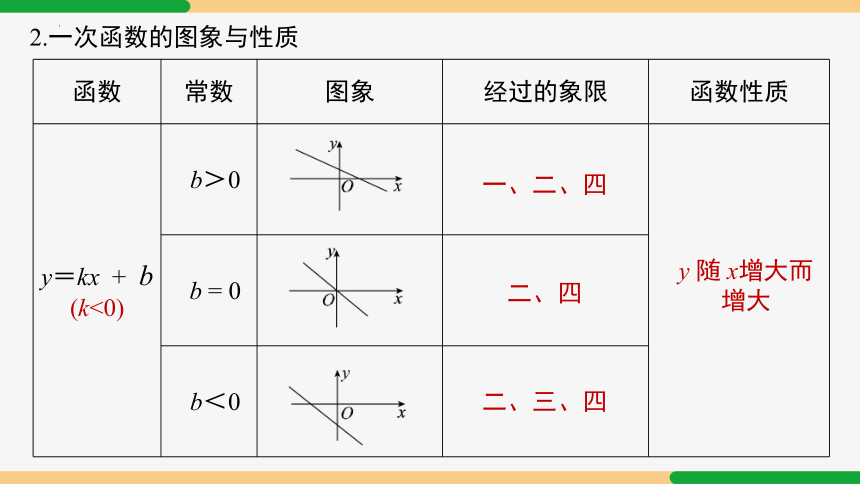
2.一次函数的图象与性质
函数 常数 图象 经过的象限 函数性质
y=kx + b (k<0) b>0
b = 0 b<0 y 随 x增大而
增大
二、四
一、二、四
二、三、四
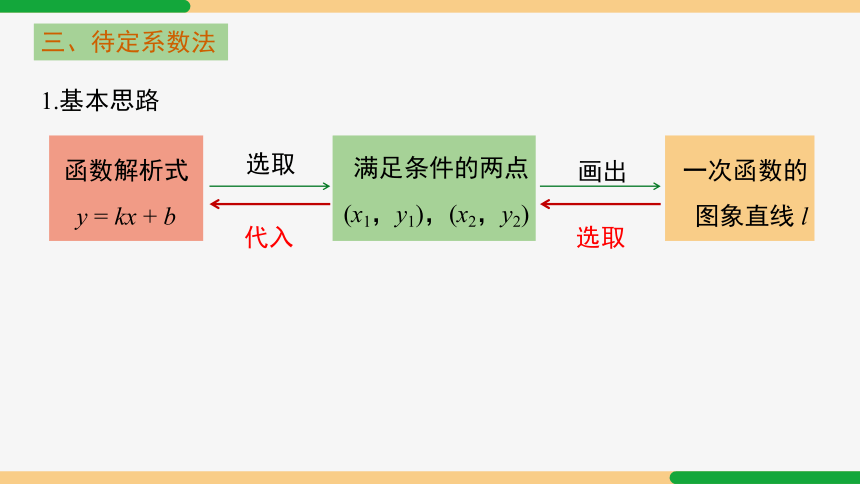
三、待定系数法
1.基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
三、待定系数法
2.基本步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
三、一次函数的应用
1.一次函数与方程的关系
方程
解一元一次方程 ax + b = 0 (a ≠ 0)
当函数y = ax + b=0 时,求自变量x的值
求直线 y =ax + b与 x 轴(y =0)交点的横坐标
函数
图象
方程
解一元一次方程 ax + b > 0 或 ax + b > 0(a ≠ 0)
求直线 y =ax + b与 x 轴(y =0)的x 轴左或右部分
函数
图象
2.一次函数与不等式的关系
3.一次函数与二元一次方程的关系
函数
一次函数 y=kx + b (k ≠ 0)
直线 y=kx + b (k ≠ 0)
二元一次方程 y -kx= b (k ≠ 0)
图象
方程
一组解
x=
y =
直线的点坐标(x, y)
二元一次方程组
两个一次函数
方程组的解
x= m
y = n
两直线的交点(m, n)
数形结合
4.一次函数与二元一次方程组的关系
方程(组)
函数
图象
不等式(组)
数 (大于、小于、等于)
形 (上下相交)
数形结合
简记:上大下小等相交
课堂练习
2.函数 中,自变量 x 的取值范围是( )
1.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的周长与面积
C.等腰三角形的底边长与面积
D.圆的周长与半径
C
A. x>3 B. x<3 C. x≤3 D. x≥-3
B
3.星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程 y(千米)和所用的时间 x(分)之间的函数关系.下列说法错误的是( )
A. 小强从家到公共汽车站步行了 2 千米
B. 小强在公共汽车站等小明用了 10 分钟
C. 公交车的平均速度是 34 千米/时
D. 小强乘公交车用了 30 分钟
C
y(千米)
x(分)
4. 一次函数 y = -5x + 2 的图象不经过第______象限.
5. 点(-1,y1),(2,y2) 是直线 y = 2x + 1 上两点, 则 y1____y2.
三
<
6.填空题:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数 y随 x 的增大而增大的是________;函数 y 随 x 的增大而减小的是_____;图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
7.方程 x + 2 = 0 的解就是函数 y = x + 2 的图象与( )
A. x 轴交点的横坐标 B. y 轴交点的横坐标
C. y 轴交点的纵坐标 D. 以上都不对
8. 两个一次函数 y = -x + 5 和 y = -2x + 8 的图象的交点坐标是 _________.
A
(3,2)
9.如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
A
10.用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
A
知识结构与要点
一次函数 章节复习
| 第1课时|
内容提要
知识结构
知识要点
针对练习
知识网络
函数
变化的世界
一次函数
性质
图象
解析式
变量
常量
建模
特例
待定系数法
函数定义
表示方法
画函数图象
正比例函数
一元一次方程
一元一次不等式
二元一次方程组
一元一次不等式组
函数观点
应用
数形结合
知识要点
一、函数
1. 常量与变量
数值发生变化的量叫变量,
数值始终不变的量叫常量.
在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
2. 函数定义:
3. 函数的图象
对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
列表法解析式法图象法
5. 函数的三种表示方法:
4. 描点法画图象的步骤:
列表、描点、连线
二、一次函数
1.一次函数与正比例函数的定义
一般地,如果 y= k x+b (k、b是常数,k ≠ 0 ),那么 y 叫做 x 的一次函数
当 b=____时,一次函数y=k x+b 变为 y= k x(k为常数, k ≠ 0),这时 y 叫做 x 的正比例函数
2.一次函数的图象与性质
函数 常数 图象 经过的象限 函数性质
y=kx + b (k>0) b>0
b = 0 b<0 y 随 x增大而
减小
一、三
一、二、三
一、三、四
2.一次函数的图象与性质
函数 常数 图象 经过的象限 函数性质
y=kx + b (k<0) b>0
b = 0 b<0 y 随 x增大而
增大
二、四
一、二、四
二、三、四
三、待定系数法
1.基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
三、待定系数法
2.基本步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
三、一次函数的应用
1.一次函数与方程的关系
方程
解一元一次方程 ax + b = 0 (a ≠ 0)
当函数y = ax + b=0 时,求自变量x的值
求直线 y =ax + b与 x 轴(y =0)交点的横坐标
函数
图象
方程
解一元一次方程 ax + b > 0 或 ax + b > 0(a ≠ 0)
求直线 y =ax + b与 x 轴(y =0)的x 轴左或右部分
函数
图象
2.一次函数与不等式的关系
3.一次函数与二元一次方程的关系
函数
一次函数 y=kx + b (k ≠ 0)
直线 y=kx + b (k ≠ 0)
二元一次方程 y -kx= b (k ≠ 0)
图象
方程
一组解
x=
y =
直线的点坐标(x, y)
二元一次方程组
两个一次函数
方程组的解
x= m
y = n
两直线的交点(m, n)
数形结合
4.一次函数与二元一次方程组的关系
方程(组)
函数
图象
不等式(组)
数 (大于、小于、等于)
形 (上下相交)
数形结合
简记:上大下小等相交
课堂练习
2.函数 中,自变量 x 的取值范围是( )
1.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的周长与面积
C.等腰三角形的底边长与面积
D.圆的周长与半径
C
A. x>3 B. x<3 C. x≤3 D. x≥-3
B
3.星期天下午,小强和小明相约在某公交车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程 y(千米)和所用的时间 x(分)之间的函数关系.下列说法错误的是( )
A. 小强从家到公共汽车站步行了 2 千米
B. 小强在公共汽车站等小明用了 10 分钟
C. 公交车的平均速度是 34 千米/时
D. 小强乘公交车用了 30 分钟
C
y(千米)
x(分)
4. 一次函数 y = -5x + 2 的图象不经过第______象限.
5. 点(-1,y1),(2,y2) 是直线 y = 2x + 1 上两点, 则 y1____y2.
三
<
6.填空题:
有下列函数:① , ② ,③ , ④ . 其中函数图象过原点的是_____;函数 y随 x 的增大而增大的是________;函数 y 随 x 的增大而减小的是_____;图象在第一、二、三象限的是______.
②
③
①②③
④
x
y
2
=
7.方程 x + 2 = 0 的解就是函数 y = x + 2 的图象与( )
A. x 轴交点的横坐标 B. y 轴交点的横坐标
C. y 轴交点的纵坐标 D. 以上都不对
8. 两个一次函数 y = -x + 5 和 y = -2x + 8 的图象的交点坐标是 _________.
A
(3,2)
9.如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
A
10.用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
A
