19.2.2 一次函数 第4课时 课件(22张PPT)
文档属性
| 名称 | 19.2.2 一次函数 第4课时 课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 41.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
用待定系数法求一次函数的解析式
19.2.2 一次函数
| 第4课时|
情景引入
求一次函数的解析式有那些题型?
知识回顾
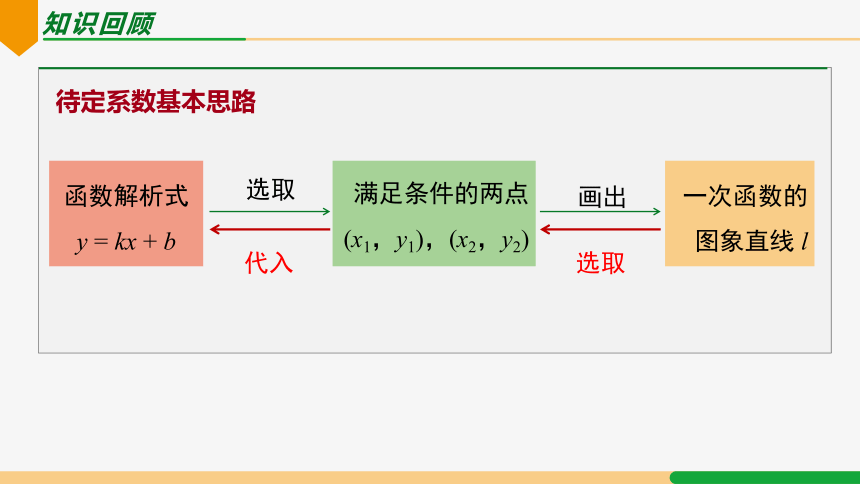
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
针对练习
例1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
例2. 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
典例讲解
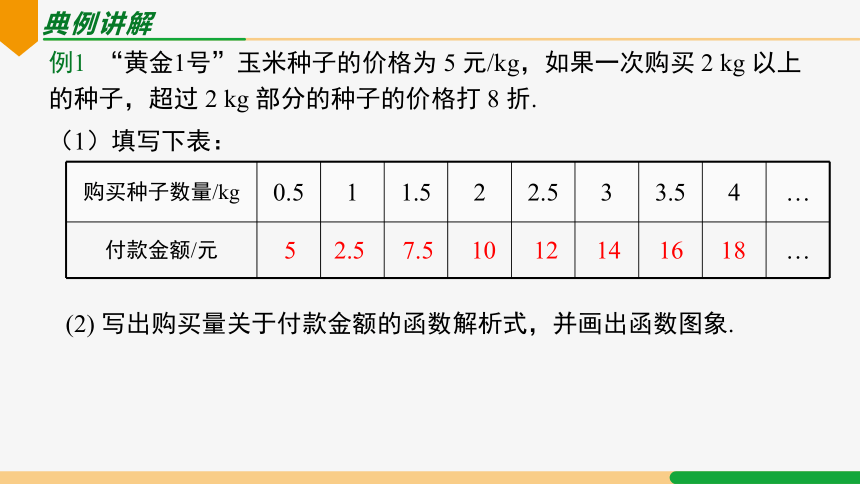
购买种子数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例1 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
y
x
O
1
2
10
3
14
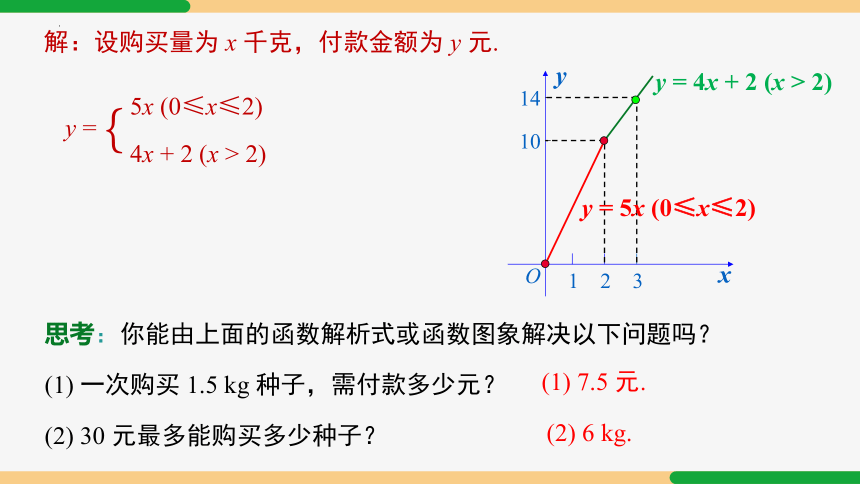
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 5×0.8(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
函数图象如右图:
y = 4x + 2 (x > 2)
y = 5x (0≤x≤2)
y
x
O
1
2
10
3
14
解:设购买量为 x 千克,付款金额为 y 元.
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 4x + 2 (x > 2)
y = 5x (0≤x≤2)
思考:你能由上面的函数解析式或函数图象解决以下问题吗?
(1) 一次购买 1.5 kg 种子,需付款多少元?
(2) 30 元最多能购买多少种子?
(1) 7.5 元.
(2) 6 kg.
例2 如图,直线y= x+ 与两坐标轴分别交于A,B 两点.
(1)求∠ABO 的度数;
(2)过A的直线l 交x 轴正半轴于C,AB=AC,求直线l 对应的函数解析式.
(1)对于直线y= x+ ,
令x=0,则y=,
令y=0,则x=-1,
故点A 的坐标为(0, ),点B 的坐标为(-1,0),
则AO= ,BO=1,
∴AB=2.
∴∠BAO=30°.
∴∠ABO=60°.
解:
课堂小结
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
线段长度
分段函数
符号
自变量
课堂练习
1.若一次函数 y=kx+b 的图象经过点(0,2)和(1,0),则这个函数的解析式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
2.根据表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )
A. 1 B.-1
C.3 D.-3
x -2 0 1
y 3 p 0
A
3.一次函数y=-2x+m 的图象经过点P (-2,3),且与x 轴,y 轴分别交于点A,B,则△AOB 的面积是( )
A. B.
C.4 D.8
B
4.一个试验室在0:00—2:00保持20 ℃的恒温,在2:00—4:00匀速升温,每小时升高5 ℃. 写出试验室温度T (单位:℃)关于时间t (单位:h)的函数解析式,并画出函数图象.
当0≤t≤2时,T=20.
当2T=20+5(t-2)=10+5t.
即T 与t 的函数解析式为
T= 函数图象如图.
5. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过 8 立方米,每立方米收取 1 元外加 0.3 元的污水处理费;超过时,超过部分每立方米收取 1.5 元外加 1.2 元污水处理费,现设一户每月用水 x 立方米,应缴水费 y 元.
(1)求出 y 关于 x 的函数解析式;
解:y 关于 x 的函数解析式为:
(1 + 0.3)x = 1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8 = 2.7x - 11.2. (x>8)
y =
(2) 当 x = 10 时,y = 2.7×10 - 11.2 = 15.8.
(3) ∵ 1.3×8 = 10.4 < 26.6,
∴ 2.7x - 11.2 = 26.6,解得 x = 14.
答:应缴水费为 15.8 元.
答:该户这月用水量为 14 立方米.
(2) 该市一户某月若用水 x = 10 立方米时,求应缴水费;
(3) 该市一户某月缴水费 26.6 元,求该户这月用水量.
∴ 该用户用水量超过 8 立方米.
6. 正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
解:(1)由题意可知,B点的坐标是(0,-5)
∵一次函数y=k2x+b的图象过点(0,-5),(3,4)
∴ , 解得
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5
因此 y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
7.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( )
A. B.
C. D.y=4
【解答】解:过D点作DH⊥x轴于H,如图,
∵点A(3,0),B(0,4).
∴OA=3,OB=4,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵∠OBA+∠OAB=90°,∠ABO+∠DAH=90°,
∴∠ABO=∠DAH,
在△ABO和△DAH中,
,
∴△ABO≌△DAH(AAS),
∴AH=OB=4,DH=OA=3,
∴D(7,3),
设直线BD的解析式为y=kx+b,
把D(7,3),B(0,4)代入得 ,
解得 ,
∴直线BD的解析式为 .
故选:A.
用待定系数法求一次函数的解析式
19.2.2 一次函数
| 第4课时|
情景引入
求一次函数的解析式有那些题型?
知识回顾
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
针对练习
例1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
例2. 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
典例讲解
购买种子数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例1 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
y
x
O
1
2
10
3
14
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 5×0.8(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
函数图象如右图:
y = 4x + 2 (x > 2)
y = 5x (0≤x≤2)
y
x
O
1
2
10
3
14
解:设购买量为 x 千克,付款金额为 y 元.
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 4x + 2 (x > 2)
y = 5x (0≤x≤2)
思考:你能由上面的函数解析式或函数图象解决以下问题吗?
(1) 一次购买 1.5 kg 种子,需付款多少元?
(2) 30 元最多能购买多少种子?
(1) 7.5 元.
(2) 6 kg.
例2 如图,直线y= x+ 与两坐标轴分别交于A,B 两点.
(1)求∠ABO 的度数;
(2)过A的直线l 交x 轴正半轴于C,AB=AC,求直线l 对应的函数解析式.
(1)对于直线y= x+ ,
令x=0,则y=,
令y=0,则x=-1,
故点A 的坐标为(0, ),点B 的坐标为(-1,0),
则AO= ,BO=1,
∴AB=2.
∴∠BAO=30°.
∴∠ABO=60°.
解:
课堂小结
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
线段长度
分段函数
符号
自变量
课堂练习
1.若一次函数 y=kx+b 的图象经过点(0,2)和(1,0),则这个函数的解析式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
2.根据表中一次函数的自变量x 与函数y 的对应值,可得p 的值为( )
A. 1 B.-1
C.3 D.-3
x -2 0 1
y 3 p 0
A
3.一次函数y=-2x+m 的图象经过点P (-2,3),且与x 轴,y 轴分别交于点A,B,则△AOB 的面积是( )
A. B.
C.4 D.8
B
4.一个试验室在0:00—2:00保持20 ℃的恒温,在2:00—4:00匀速升温,每小时升高5 ℃. 写出试验室温度T (单位:℃)关于时间t (单位:h)的函数解析式,并画出函数图象.
当0≤t≤2时,T=20.
当2
即T 与t 的函数解析式为
T= 函数图象如图.
5. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过 8 立方米,每立方米收取 1 元外加 0.3 元的污水处理费;超过时,超过部分每立方米收取 1.5 元外加 1.2 元污水处理费,现设一户每月用水 x 立方米,应缴水费 y 元.
(1)求出 y 关于 x 的函数解析式;
解:y 关于 x 的函数解析式为:
(1 + 0.3)x = 1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8 = 2.7x - 11.2. (x>8)
y =
(2) 当 x = 10 时,y = 2.7×10 - 11.2 = 15.8.
(3) ∵ 1.3×8 = 10.4 < 26.6,
∴ 2.7x - 11.2 = 26.6,解得 x = 14.
答:应缴水费为 15.8 元.
答:该户这月用水量为 14 立方米.
(2) 该市一户某月若用水 x = 10 立方米时,求应缴水费;
(3) 该市一户某月缴水费 26.6 元,求该户这月用水量.
∴ 该用户用水量超过 8 立方米.
6. 正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
解:(1)由题意可知,B点的坐标是(0,-5)
∵一次函数y=k2x+b的图象过点(0,-5),(3,4)
∴ , 解得
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5
因此 y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
7.在平面直角坐标系中,点A(3,0),B(0,4).以AB为一边在第一象限作正方形ABCD,则对角线BD所在直线的解析式为( )
A. B.
C. D.y=4
【解答】解:过D点作DH⊥x轴于H,如图,
∵点A(3,0),B(0,4).
∴OA=3,OB=4,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵∠OBA+∠OAB=90°,∠ABO+∠DAH=90°,
∴∠ABO=∠DAH,
在△ABO和△DAH中,
,
∴△ABO≌△DAH(AAS),
∴AH=OB=4,DH=OA=3,
∴D(7,3),
设直线BD的解析式为y=kx+b,
把D(7,3),B(0,4)代入得 ,
解得 ,
∴直线BD的解析式为 .
故选:A.
