第19章 一次函数复习 第3课时 课件(17张PPT)
文档属性
| 名称 | 第19章 一次函数复习 第3课时 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览






文档简介
一次函数与方程、不等式
一次函数 章节复习
| 第3课时|
考点一 一次函数与一元一次方程
一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
?
A
?
考点二 一次函数与一元一次不等式
已知一次函数 y=ax+b 与 x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则关于 x 的不等式 ax+b>0 的解集是( ).
A.x>-2 B. x<-2
A
C.x>4 D.x<4
考点三 一次函数与二元一次方程(组)
用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
A
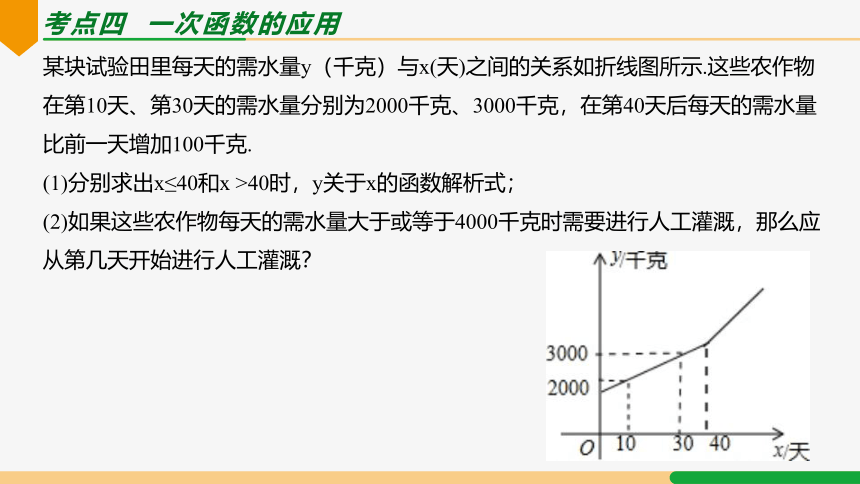
考点四 一次函数的应用
某块试验田里每天的需水量y(千克)与x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x >40时,y关于x的函数解析式;
(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
根据题意,得
解:(1)当x≤40 时,设y=kx+b
解这个方程组,得
当x≤40时,y关于x的函数解析式是:y=50x+1500
当 x=40 时, y=50× 40+1500=3500
当x≥40 时,根据题意,得 y=100(x-40)+3500
即y=100x-500
∴当 x≥40 时, y 与 x 之间的关系式是:y=100x-500
(1) 当 y≥40 00 时, y与x之间的关系式是 y=100x-500
∴应从第45天开始进行人工灌溉.
列不等式 100x-500≥40 00
解得x≥45
当x≥40 时,根据题意,得 y=100(x-40)+3500
考点五 综合求解析式
如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式.
解:设点P坐标为(-1,a),
把P(-1,a)代入y=2x+3,得a=1,
∴点P(-1,1),
设直线l2的函数表达式为y=kx+b,
把P(-1,1)、A(0,-1)分别代入y=kx+b,得
?k+b=1b=?1,解得k=?2b=?1?
∴直线l2的函数表达式为y=-2x-1.
?
已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y≤9,求这个一次函数解析式.
解:设该一次函数的关系式是:y=kx+b(k≠0).
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,
相应函数值的取值范围是:5≤y≤9,则
①当k>0时,x=2时,y=5;x=6时,y=9.
根据题意列出方程组:2k+b=56k+b=9
解得k=1b=3?
则这个函数的解析式是:y=x+3;
?
②当k<0时, x=2时,y=9;x=6时,y=5.
根据题意列出方程组:
则2k+b=96k+b=5
解得k=?1b=11?
所以该一次函数的解析式为y=-x+11,
?
综上所述,该一次函数的解析式是y=x+3或y=-x+11.
已知一次函数的图象经过点(0,-2),且与两条坐标轴围成三角形的面积是4,试求一次函数的解析式.
解:根据题意画出相应的图形,如图所示:
由一次函数过(0,-2),设一次函数解析式为y=kx-2(k≠0),
令y=0,解得:x=2????,
又一次函数与两坐标轴围成的三角形面积为4,
∴12×|-2|×| 2?????|=4,即|k|= 12?,
解得:k=± 12?,
则一次函数解析式为y= 12?x-2或y=- 12?x-2.
?
考点六 一次函数与几何综合应用
如图,在平面直角坐标系xOy中,直线y=-43 x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式.
?
(1)求AB的长和点C的坐标.
解:(1)∵直线y=-43x+8与x轴,y轴分别交于点A,点B,
∴A(6,0),B(0,8),
在Rt△OAB中,∠AOB=90°,OA=6,OB=8,
∴AB=62+82=10,
∵△DAB沿直线AD折叠后的对应三角形为△DAC,
∴AC=AB=10,
∴OC=OA+AC=OA+AB=16,
∵点C在x轴的正半轴上,
∴点C的坐标为C(16,0).
?
(2)求直线CD的解析式.
(2)设点D的坐标为D(0,a)(a<0),
由题意可知CD=BD,CD2=BD2,
在Rt△OCD中,由勾股定理得162+y2=(8-y)2,
解得a=-12.
∴点D的坐标为D(0,-12),
可设直线CD的解析式为 y=kx-12(k≠0)
∵点C(16,0)在直线y=kx-12上,
∴16k-12=0,
解得k=34,
∴直线CD的解析式为y= 34?x-12.
一次函数 章节复习
| 第3课时|
考点一 一次函数与一元一次方程
一元一次方程 ax-b=0 的解为 x=5,则函数 y=ax-b 与 x 轴的交点坐标是( ).
A.(0,5) B.(0 ,-5)
C
C.(5,0) D.(-5 ,0)
如图,一次函数y=2x+1的图象与坐标轴分别交于A、B两点,O为坐标原点,则△AOB的面积是( ).
?
A
?
考点二 一次函数与一元一次不等式
已知一次函数 y=ax+b 与 x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),则关于 x 的不等式 ax+b>0 的解集是( ).
A.x>-2 B. x<-2
A
C.x>4 D.x<4
考点三 一次函数与二元一次方程(组)
用图象法解某二元一次方程组时,在同一直角坐标系中画出相应的两个一次函数的图象,则所解的二元一次方程组是( ).
x+y-2=0
3x-2y-1=0
A.
2x-y-1=0
3x-2y-1=0
B.
2x-y-1=0
3x+2y-5=0
C.
x+y-2=0
2x-y-1=0
D.
A
考点四 一次函数的应用
某块试验田里每天的需水量y(千克)与x(天)之间的关系如折线图所示.这些农作物在第10天、第30天的需水量分别为2000千克、3000千克,在第40天后每天的需水量比前一天增加100千克.
(1)分别求出x≤40和x >40时,y关于x的函数解析式;
(2)如果这些农作物每天的需水量大于或等于4000千克时需要进行人工灌溉,那么应从第几天开始进行人工灌溉?
根据题意,得
解:(1)当x≤40 时,设y=kx+b
解这个方程组,得
当x≤40时,y关于x的函数解析式是:y=50x+1500
当 x=40 时, y=50× 40+1500=3500
当x≥40 时,根据题意,得 y=100(x-40)+3500
即y=100x-500
∴当 x≥40 时, y 与 x 之间的关系式是:y=100x-500
(1) 当 y≥40 00 时, y与x之间的关系式是 y=100x-500
∴应从第45天开始进行人工灌溉.
列不等式 100x-500≥40 00
解得x≥45
当x≥40 时,根据题意,得 y=100(x-40)+3500
考点五 综合求解析式
如图,直线l1与l2相交于点P,l1的函数表达式y=2x+3,点P的横坐标为-1,且l2交y轴于点A(0,-1).求直线l2的函数表达式.
解:设点P坐标为(-1,a),
把P(-1,a)代入y=2x+3,得a=1,
∴点P(-1,1),
设直线l2的函数表达式为y=kx+b,
把P(-1,1)、A(0,-1)分别代入y=kx+b,得
?k+b=1b=?1,解得k=?2b=?1?
∴直线l2的函数表达式为y=-2x-1.
?
已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y≤9,求这个一次函数解析式.
解:设该一次函数的关系式是:y=kx+b(k≠0).
一次函数y=kx+b的自变量的取值范围是:2≤x≤6,
相应函数值的取值范围是:5≤y≤9,则
①当k>0时,x=2时,y=5;x=6时,y=9.
根据题意列出方程组:2k+b=56k+b=9
解得k=1b=3?
则这个函数的解析式是:y=x+3;
?
②当k<0时, x=2时,y=9;x=6时,y=5.
根据题意列出方程组:
则2k+b=96k+b=5
解得k=?1b=11?
所以该一次函数的解析式为y=-x+11,
?
综上所述,该一次函数的解析式是y=x+3或y=-x+11.
已知一次函数的图象经过点(0,-2),且与两条坐标轴围成三角形的面积是4,试求一次函数的解析式.
解:根据题意画出相应的图形,如图所示:
由一次函数过(0,-2),设一次函数解析式为y=kx-2(k≠0),
令y=0,解得:x=2????,
又一次函数与两坐标轴围成的三角形面积为4,
∴12×|-2|×| 2?????|=4,即|k|= 12?,
解得:k=± 12?,
则一次函数解析式为y= 12?x-2或y=- 12?x-2.
?
考点六 一次函数与几何综合应用
如图,在平面直角坐标系xOy中,直线y=-43 x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式.
?
(1)求AB的长和点C的坐标.
解:(1)∵直线y=-43x+8与x轴,y轴分别交于点A,点B,
∴A(6,0),B(0,8),
在Rt△OAB中,∠AOB=90°,OA=6,OB=8,
∴AB=62+82=10,
∵△DAB沿直线AD折叠后的对应三角形为△DAC,
∴AC=AB=10,
∴OC=OA+AC=OA+AB=16,
∵点C在x轴的正半轴上,
∴点C的坐标为C(16,0).
?
(2)求直线CD的解析式.
(2)设点D的坐标为D(0,a)(a<0),
由题意可知CD=BD,CD2=BD2,
在Rt△OCD中,由勾股定理得162+y2=(8-y)2,
解得a=-12.
∴点D的坐标为D(0,-12),
可设直线CD的解析式为 y=kx-12(k≠0)
∵点C(16,0)在直线y=kx-12上,
∴16k-12=0,
解得k=34,
∴直线CD的解析式为y= 34?x-12.
