第19章 一次函数复习 第2课时 课件(22张PPT)
文档属性
| 名称 | 第19章 一次函数复习 第2课时 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 952.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 09:41:06 | ||
图片预览








文档简介
(共22张PPT)
一次函数图象及性质
一次函数 章节复习
| 第2课时|
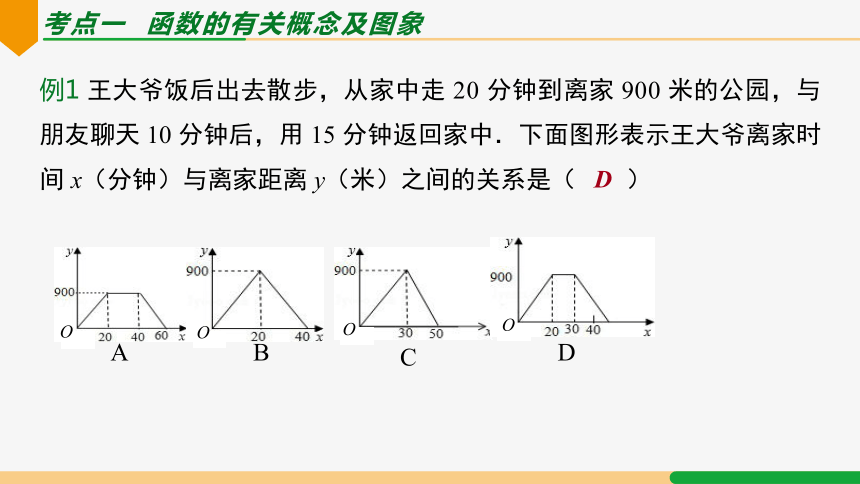
考点一 函数的有关概念及图象
例1 王大爷饭后出去散步,从家中走 20 分钟到离家 900 米的公园,与朋友聊天 10 分钟后,用 15 分钟返回家中.下面图形表示王大爷离家时间 x(分钟)与离家距离 y(米)之间的关系是( )
A
B
C
D
D
O
O
O
O
考点二 一次函数的图象与性质
例2 已知函数 y = (2m + 1)x + m﹣3;
(1)若该函数是正比例函数,求 m 的值;
(2)若函数的图象平行直线 y = 3x﹣3,求 m 的值;
(3)若这个函数是一次函数,且 y 随着 x 的增大而减小,求 m 的取值范围
(4)若这个函数图象过点 (1,4),求这个函数的解析式.
解:(1) ∵函数是正比例函数,
∴m﹣3 = 0,且 2m + 1≠ 0,解得 m = 3.
(2) ∵ 函数的图象平行于直线 y = 3x﹣3,
∴ 2m + 1 = 3,解得 m = 1.
(3) ∵ y 随着 x 的增大而减小,
∴ 2m + 1<0,解得 m< .
(4)∵ 该函数图象过点 (1,4),代入得 2m + 1 + m - 3 = 4,
解得 m = 2,∴该函数的解析式为 y = 5x - 1.
考点三 一次函数的平移规律
1.若将直线y=kx(k≠0)的图象向上平移3个单位长度后经过点(2,7),则平移后直线的解析式为( )
A.y=2x+3 B.y=5x+3 C.y=5x-3 D.y=2x-3
A
2.直线y=-2x+1向____平移_____个单位长度所得直线的解析式为
y=-2x-4.
下
5
考点四 一次函数与方程、不等式
例3 如图,一次函数 y1 = x + b 与一次函数 y2 = kx + 4 的图象交于点 P(1,3),则关于 x 的不等式x + b>kx + 4 的解集是( )
y
A.x>﹣2 B.x>0
C.x>1 D.x<1
x
O
y1=x+b
y2=kx+4
P
1
3
C
考点五 待定系数法求一次函数解析式
例4 已知一次函数的图象经过点A(2,1),且与直线y=-2x-3平行,求这个一次函数的表达式.
解:设一次函数的解析式是y=kx+b(k≠0),由题意得,
解得
因此这个一次函数的表达式为:y=-2x+5.
例5 A(1,3) 、B(-2,0) 、C(-4,-2)三点是否在同一条直线上?为什么?
解:设该直线的函数解析式是y=kx+b,
把点A(1,3) 、B(-2,0)代入得:
解得
∴此函数解析式是:y=x+2,
当x=-4时,y=-4+2=-2,
∴点C在此直线上,
即:A、B、C三点在同一条直线上.
考点六 一次函数的应用
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是 960 元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例6 为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
解得
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值,为
33×800+17×960=42720(元).
即最低成本是 42720 元.
针对练习
1.下列所有解析式中,是一次函数但不是正比例函数的是( )
B
2.正比例函数 y=-2x 的图象经过的象限是 ,
一次函数 y=2x+4 的图象经过的象限是 .
二、四象限
一、二、三象限
5.点 P1 ( x1 , y1 ), P2 ( x2 , y2 )是一次函数y=-2x-5图象上的两个点,且 x1 < x2 ,则 y1 与 y2 的大小关系是___________ .
y 1 >y 2
3.已知一次函数 y=(m+3)x+2n 经过点(0,4)和点(-1,0),求这个函数解析式.
解:因为一次函数 y=(m+3)x+2n 经过点(0,4)和点(-1,0)
2n=4
-(m+3)+2n=0
所以
n=2
m=1
解得
所以一次函数解析式为 y=4x+4.
4.已知一次函数 y=kx+b 经过点(2,4)和点(0,-1),求这个函数解析式.
解:因为一次函数 y=kx+b经过点(2,4)和点(0,-1)
2k+b=4
b=-1
所以
b=-1
解得
1.下列图形中,表示一次函数 y=mx+n 与正比例函数y=mnx(m、n为常数,且mn≠0)的图象的是( )
A
2.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值是,y是x的正比例函数.
解:由函数是一次函数可得,
m+1≠0,解得 m≠-1,
所以,m≠-1时,y是x的一次函数;
函数为正比例函数时,
m+1≠0且m2-1=0,解得 m=1,
所以,当m=1时,y是x的正比例函数.
3.如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )
A.a>b>c B.c>b>a C.b>a>c D.b>c>a
B
4.如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象. (1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
5.已知函数y=(2m+1)x+m﹣3;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行直线y=3x﹣3,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
解:(1)m=3.
(2)m=1.
(3)m<0.5.
(4)y=5x-1.
解:(1)∵函数是正比例函数,∴m﹣3=0,且2m+1≠0,
解得m=3.
(2)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1.
(3)∵y随着x的增大而减小,∴2m+1<0,解得m< .
(4)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴该函数的解析式为y=5x-1.
6.已知一次函数y=(2m+1)x-m-1 的图象不经过第三象限,则m的取值范围是_________.
m≤-1
解:当一次函数只经过二、四象限时:解得:m=-1;
当一次函数经过一、二、四象限时:解得:m<-1;
综上可以得到:m≤-1.
一次函数图象及性质
一次函数 章节复习
| 第2课时|
考点一 函数的有关概念及图象
例1 王大爷饭后出去散步,从家中走 20 分钟到离家 900 米的公园,与朋友聊天 10 分钟后,用 15 分钟返回家中.下面图形表示王大爷离家时间 x(分钟)与离家距离 y(米)之间的关系是( )
A
B
C
D
D
O
O
O
O
考点二 一次函数的图象与性质
例2 已知函数 y = (2m + 1)x + m﹣3;
(1)若该函数是正比例函数,求 m 的值;
(2)若函数的图象平行直线 y = 3x﹣3,求 m 的值;
(3)若这个函数是一次函数,且 y 随着 x 的增大而减小,求 m 的取值范围
(4)若这个函数图象过点 (1,4),求这个函数的解析式.
解:(1) ∵函数是正比例函数,
∴m﹣3 = 0,且 2m + 1≠ 0,解得 m = 3.
(2) ∵ 函数的图象平行于直线 y = 3x﹣3,
∴ 2m + 1 = 3,解得 m = 1.
(3) ∵ y 随着 x 的增大而减小,
∴ 2m + 1<0,解得 m< .
(4)∵ 该函数图象过点 (1,4),代入得 2m + 1 + m - 3 = 4,
解得 m = 2,∴该函数的解析式为 y = 5x - 1.
考点三 一次函数的平移规律
1.若将直线y=kx(k≠0)的图象向上平移3个单位长度后经过点(2,7),则平移后直线的解析式为( )
A.y=2x+3 B.y=5x+3 C.y=5x-3 D.y=2x-3
A
2.直线y=-2x+1向____平移_____个单位长度所得直线的解析式为
y=-2x-4.
下
5
考点四 一次函数与方程、不等式
例3 如图,一次函数 y1 = x + b 与一次函数 y2 = kx + 4 的图象交于点 P(1,3),则关于 x 的不等式x + b>kx + 4 的解集是( )
y
A.x>﹣2 B.x>0
C.x>1 D.x<1
x
O
y1=x+b
y2=kx+4
P
1
3
C
考点五 待定系数法求一次函数解析式
例4 已知一次函数的图象经过点A(2,1),且与直线y=-2x-3平行,求这个一次函数的表达式.
解:设一次函数的解析式是y=kx+b(k≠0),由题意得,
解得
因此这个一次函数的表达式为:y=-2x+5.
例5 A(1,3) 、B(-2,0) 、C(-4,-2)三点是否在同一条直线上?为什么?
解:设该直线的函数解析式是y=kx+b,
把点A(1,3) 、B(-2,0)代入得:
解得
∴此函数解析式是:y=x+2,
当x=-4时,y=-4+2=-2,
∴点C在此直线上,
即:A、B、C三点在同一条直线上.
考点六 一次函数的应用
(1)问符合题意的搭配方案有几种?请你帮助设计出来;
(2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型的成本是 960 元,试说明(1)中哪种方案成本最低?最低成本是多少元?
例6 为美化深圳市景,园林部门决定利用现有的 3490 盆甲种花卉和 2950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆.
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
依题意,得
∴31≤x≤33.
∵x 是整数,x 可取 31,32,33,
∴可设计三种搭配方案:
①A 种园艺造型 31 个,B 种园艺造型 19 个;
②A 种园艺造型 32 个,B 种园艺造型 18 个;
③A 种园艺造型 33 个,B 种园艺造型 17 个.
解得
方案①需成本:31×800+19×960=43040(元);
方案②需成本:32×800+18×960=42880(元);
方案③需成本:33×800+17×960=42720(元).
(2)方法一:
方法二:成本为
y=800x+960(50-x)=-160x+48000(31≤x≤33).
根据一次函数的性质,y 随 x 的增大而减小,
故当 x=33 时,y 取得最小值,为
33×800+17×960=42720(元).
即最低成本是 42720 元.
针对练习
1.下列所有解析式中,是一次函数但不是正比例函数的是( )
B
2.正比例函数 y=-2x 的图象经过的象限是 ,
一次函数 y=2x+4 的图象经过的象限是 .
二、四象限
一、二、三象限
5.点 P1 ( x1 , y1 ), P2 ( x2 , y2 )是一次函数y=-2x-5图象上的两个点,且 x1 < x2 ,则 y1 与 y2 的大小关系是___________ .
y 1 >y 2
3.已知一次函数 y=(m+3)x+2n 经过点(0,4)和点(-1,0),求这个函数解析式.
解:因为一次函数 y=(m+3)x+2n 经过点(0,4)和点(-1,0)
2n=4
-(m+3)+2n=0
所以
n=2
m=1
解得
所以一次函数解析式为 y=4x+4.
4.已知一次函数 y=kx+b 经过点(2,4)和点(0,-1),求这个函数解析式.
解:因为一次函数 y=kx+b经过点(2,4)和点(0,-1)
2k+b=4
b=-1
所以
b=-1
解得
1.下列图形中,表示一次函数 y=mx+n 与正比例函数y=mnx(m、n为常数,且mn≠0)的图象的是( )
A
2.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值是,y是x的正比例函数.
解:由函数是一次函数可得,
m+1≠0,解得 m≠-1,
所以,m≠-1时,y是x的一次函数;
函数为正比例函数时,
m+1≠0且m2-1=0,解得 m=1,
所以,当m=1时,y是x的正比例函数.
3.如图,三个正比例函数的图象对应的解析式为①y=ax,②y=bx,③y=cx,则a、b、c的大小关系是( )
A.a>b>c B.c>b>a C.b>a>c D.b>c>a
B
4.如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象. (1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
5.已知函数y=(2m+1)x+m﹣3;
(1)若该函数是正比例函数,求m的值;
(2)若函数的图象平行直线y=3x﹣3,求m的值;
(3)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(4)若这个函数图象过点(1,4),求这个函数的解析式.
解:(1)m=3.
(2)m=1.
(3)m<0.5.
(4)y=5x-1.
解:(1)∵函数是正比例函数,∴m﹣3=0,且2m+1≠0,
解得m=3.
(2)∵函数的图象平行于直线y=3x﹣3,∴2m+1=3,
解得m=1.
(3)∵y随着x的增大而减小,∴2m+1<0,解得m< .
(4)∵该函数图象过点(1,4),代入得2m+1+m-3=4,
解得m=2,∴该函数的解析式为y=5x-1.
6.已知一次函数y=(2m+1)x-m-1 的图象不经过第三象限,则m的取值范围是_________.
m≤-1
解:当一次函数只经过二、四象限时:解得:m=-1;
当一次函数经过一、二、四象限时:解得:m<-1;
综上可以得到:m≤-1.
