19.3 课题学习 选择方案 课件(20张PPT)
文档属性
| 名称 | 19.3 课题学习 选择方案 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 40.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
选择方案
19.3 课题学习
| 第1课时|
知识回顾
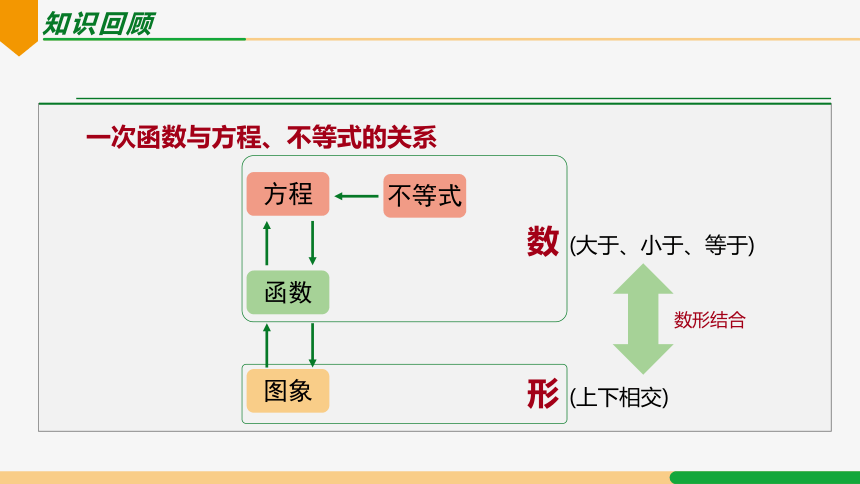
一次函数与方程、不等式的关系
方程
函数
图象
不等式
数 (大于、小于、等于)
形 (上下相交)
数形结合
典例讲解
例1 已知函数y1=2x-5,y2=3-2x,求当x 取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
解法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2;
(2)y1=y2,即2x-5=3-2x,解得x=2;
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
方法二:图象法.
在同一直角坐标系内画出函数y1=2x-5和y2=3-2x 的图象,如图所示.
由图象知,两直线的交点坐标为(2,-1).
观察图象可知,
当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
例1 已知函数y1=2x-5,y2=3-2x,求当x 取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
-1
-2
-3
3
2
1
2
1
-4
O
x
y
-1
3
4
5
-4
-5
3
-2
-3
y1 = 2x + 1
y2 = 3-2x
问题导入
一次函数在生活有什么应用
典例讲解
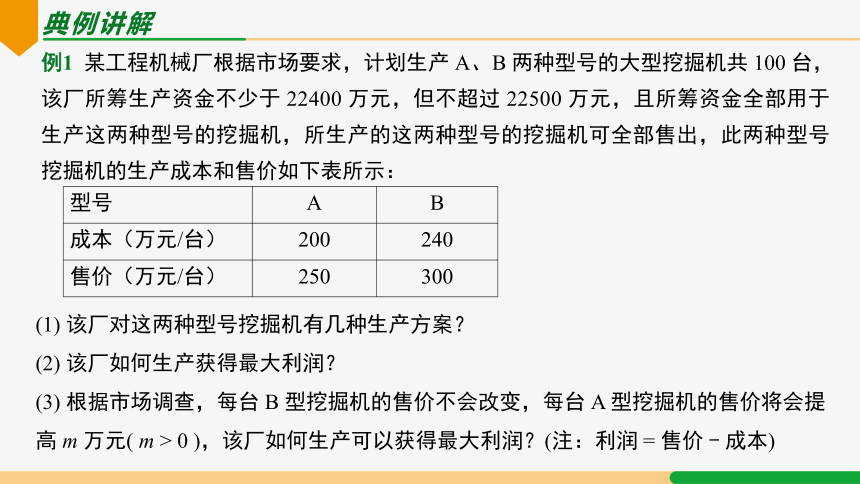
例1 某工程机械厂根据市场要求,计划生产 A、B 两种型号的大型挖掘机共 100 台,该厂所筹生产资金不少于 22400 万元,但不超过 22500 万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1) 该厂对这两种型号挖掘机有几种生产方案?
(2) 该厂如何生产获得最大利润?
(3) 根据市场调查,每台 B 型挖掘机的售价不会改变,每台 A 型挖掘机的售价将会提高 m 万元( m > 0 ),该厂如何生产可以获得最大利润?(注:利润 = 售价 - 成本)
解:(1) 设生产 A 型挖掘机 x 台,则 B 型挖掘机可生产 (100 - x) 台,由题意知:
(1) 该厂对这两种型号挖掘机有几种生产方案?
∴有三种生产方案:A 型 38 台,B 型 62 台; A 型 39 台,B 型 61 台;A型 40 台, B型 60 台.
解得 37.5≤x≤40
∵ x 取正整数, ∴ x 为 38、39、40.
∴当 x = 38 时,W最大 = 5620 (万元).
即生产 A 型 38 台,B 型 62 台时,获得最大利润.
(2) 该厂如何生产获得最大利润?
W = 50x+60(100-x)
= -10x+6000
解:设获得利润为 W (万元),由题意知:
(3) 根据市场调查,每台 B 型挖掘机的售价不会改变,每台 A 型挖掘机的售价将会提高 m 万元(m > 0),该厂如何生产可以获得最大利润?
③当 m>10 时,取 x = 40,W 最大,
即 A 型挖掘机生产 40 台,B 型生产 60 台.
解:由题意知:W = (50+m)x+60(100-x)
= (m-10)x+6000
∴① 当 0<m<10 时,取 x = 38,W 最大 ,
即 A 型挖掘机生产 38 台,B 型挖掘机生产 62 台;
②当 m = 10 时,m - 10 = 0,三种生产获得利润相等;
典例讲解
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出 A,B,C 三种上宽带网的收费方式.
选取哪种方式能节省上网费?
当 x>25 时,y1 = 30 + 0.05×60(x - 25) = 3x - 45.
合起来可写为:
当 0≤x≤25 时,y1= 30;
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
y3 = 120, (x≥0)
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
在同一坐标系画出它们的图象:
y3 = 120, (x≥0)
当上网时间__________时,选择方式 A 最省钱.
当上网时间__________时,选择方式 B 最省钱.
当上网时间_________时,选择方式 C 最省钱.
课堂小结
分析实际问题中的数量关系
建立一次函数
数学模型
探求解决实际问题的最优方案
寻求可以反映实际问题的_________
模型观念
数形结合
函数
分析变量间的关系
选取一个取值能够影响其他变量值的变量作为自变量
寻求可以反映实际问题的函数
课堂练习
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
某商场分两次购进A、B 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) 购进所需
费用(元)
A B 第一次 30 40 3 800
第二次 40 30 3 200
(1)求A、B 两种商品每件的进价分别是多少元.
(2)商场决定A 种商品以每件30元出售,B 种商品以每件100元出售.为满足市场需求,需购进A、B 两种商品共1 000件,且A 种商品的数量不少于B 种商品数量的4倍,请你求出获利最大的 进货方案,并确定最大利润.
解:
(1)设A 种商品每件的进价为x 元,B 种商品每件的进价 为y 元,
根据题意得:
解得:
答:A 种商品每件的进价为20元,B 种商品每件的进 价为80元.
解:
设购进B 种商品m 件,获得的利润为w 元,则购进A 种商品(1 000-m)件,
根据题意得:
w=(30-20)(1 000-m)+(100-80)m=10m+10 000.
∵A 种商品的数量不少于B 种商品数量的4倍,
∴1 000-m≥4m,
解得:m≤200.
∵在w=10m+10 000中,k=10>0,
∴w 的值随m 的增大而增大,
∴当m=200时,w 取最大值,
最大值为10×200+10 000=12 000.
答:当购进A 种商品800件,B 种商品200件时,销售利润最大,最大利润为12 000元.
张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择,如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x 个甲种文具时,需购买y 个乙种文具.
(1)①当减少购买1个甲种文具时,x=_____,y=_____;
②求y 与x 之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元,甲、乙两种文具各购买了多少个?
99
2
②由题意得y=2(100-x )=-2x+200,
∴y 与x 之间的函数表达式为y=-2x+200.
(2)由题意得
解得
答:甲、乙两种文具各购买了60个和80个.
解:
选择方案
19.3 课题学习
| 第1课时|
知识回顾
一次函数与方程、不等式的关系
方程
函数
图象
不等式
数 (大于、小于、等于)
形 (上下相交)
数形结合
典例讲解
例1 已知函数y1=2x-5,y2=3-2x,求当x 取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
解法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2;
(2)y1=y2,即2x-5=3-2x,解得x=2;
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
方法二:图象法.
在同一直角坐标系内画出函数y1=2x-5和y2=3-2x 的图象,如图所示.
由图象知,两直线的交点坐标为(2,-1).
观察图象可知,
当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
例1 已知函数y1=2x-5,y2=3-2x,求当x 取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
-1
-2
-3
3
2
1
2
1
-4
O
x
y
-1
3
4
5
-4
-5
3
-2
-3
y1 = 2x + 1
y2 = 3-2x
问题导入
一次函数在生活有什么应用
典例讲解
例1 某工程机械厂根据市场要求,计划生产 A、B 两种型号的大型挖掘机共 100 台,该厂所筹生产资金不少于 22400 万元,但不超过 22500 万元,且所筹资金全部用于生产这两种型号的挖掘机,所生产的这两种型号的挖掘机可全部售出,此两种型号挖掘机的生产成本和售价如下表所示:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
(1) 该厂对这两种型号挖掘机有几种生产方案?
(2) 该厂如何生产获得最大利润?
(3) 根据市场调查,每台 B 型挖掘机的售价不会改变,每台 A 型挖掘机的售价将会提高 m 万元( m > 0 ),该厂如何生产可以获得最大利润?(注:利润 = 售价 - 成本)
解:(1) 设生产 A 型挖掘机 x 台,则 B 型挖掘机可生产 (100 - x) 台,由题意知:
(1) 该厂对这两种型号挖掘机有几种生产方案?
∴有三种生产方案:A 型 38 台,B 型 62 台; A 型 39 台,B 型 61 台;A型 40 台, B型 60 台.
解得 37.5≤x≤40
∵ x 取正整数, ∴ x 为 38、39、40.
∴当 x = 38 时,W最大 = 5620 (万元).
即生产 A 型 38 台,B 型 62 台时,获得最大利润.
(2) 该厂如何生产获得最大利润?
W = 50x+60(100-x)
= -10x+6000
解:设获得利润为 W (万元),由题意知:
(3) 根据市场调查,每台 B 型挖掘机的售价不会改变,每台 A 型挖掘机的售价将会提高 m 万元(m > 0),该厂如何生产可以获得最大利润?
③当 m>10 时,取 x = 40,W 最大,
即 A 型挖掘机生产 40 台,B 型生产 60 台.
解:由题意知:W = (50+m)x+60(100-x)
= (m-10)x+6000
∴① 当 0<m<10 时,取 x = 38,W 最大 ,
即 A 型挖掘机生产 38 台,B 型挖掘机生产 62 台;
②当 m = 10 时,m - 10 = 0,三种生产获得利润相等;
典例讲解
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出 A,B,C 三种上宽带网的收费方式.
选取哪种方式能节省上网费?
当 x>25 时,y1 = 30 + 0.05×60(x - 25) = 3x - 45.
合起来可写为:
当 0≤x≤25 时,y1= 30;
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
y3 = 120, (x≥0)
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
在同一坐标系画出它们的图象:
y3 = 120, (x≥0)
当上网时间__________时,选择方式 A 最省钱.
当上网时间__________时,选择方式 B 最省钱.
当上网时间_________时,选择方式 C 最省钱.
课堂小结
分析实际问题中的数量关系
建立一次函数
数学模型
探求解决实际问题的最优方案
寻求可以反映实际问题的_________
模型观念
数形结合
函数
分析变量间的关系
选取一个取值能够影响其他变量值的变量作为自变量
寻求可以反映实际问题的函数
课堂练习
1.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
某商场分两次购进A、B 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) 购进所需
费用(元)
A B 第一次 30 40 3 800
第二次 40 30 3 200
(1)求A、B 两种商品每件的进价分别是多少元.
(2)商场决定A 种商品以每件30元出售,B 种商品以每件100元出售.为满足市场需求,需购进A、B 两种商品共1 000件,且A 种商品的数量不少于B 种商品数量的4倍,请你求出获利最大的 进货方案,并确定最大利润.
解:
(1)设A 种商品每件的进价为x 元,B 种商品每件的进价 为y 元,
根据题意得:
解得:
答:A 种商品每件的进价为20元,B 种商品每件的进 价为80元.
解:
设购进B 种商品m 件,获得的利润为w 元,则购进A 种商品(1 000-m)件,
根据题意得:
w=(30-20)(1 000-m)+(100-80)m=10m+10 000.
∵A 种商品的数量不少于B 种商品数量的4倍,
∴1 000-m≥4m,
解得:m≤200.
∵在w=10m+10 000中,k=10>0,
∴w 的值随m 的增大而增大,
∴当m=200时,w 取最大值,
最大值为10×200+10 000=12 000.
答:当购进A 种商品800件,B 种商品200件时,销售利润最大,最大利润为12 000元.
张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择,如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x 个甲种文具时,需购买y 个乙种文具.
(1)①当减少购买1个甲种文具时,x=_____,y=_____;
②求y 与x 之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元,甲、乙两种文具各购买了多少个?
99
2
②由题意得y=2(100-x )=-2x+200,
∴y 与x 之间的函数表达式为y=-2x+200.
(2)由题意得
解得
答:甲、乙两种文具各购买了60个和80个.
解:
