19.2.2 一次函数第3课时(待定系数法) 课件(17张PPT)
文档属性
| 名称 | 19.2.2 一次函数第3课时(待定系数法) 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 42.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
用待定系数法求一次函数的解析式
19.2.2 一次函数
| 第3课时|
情景引入
怎样求一次函数的解析式?
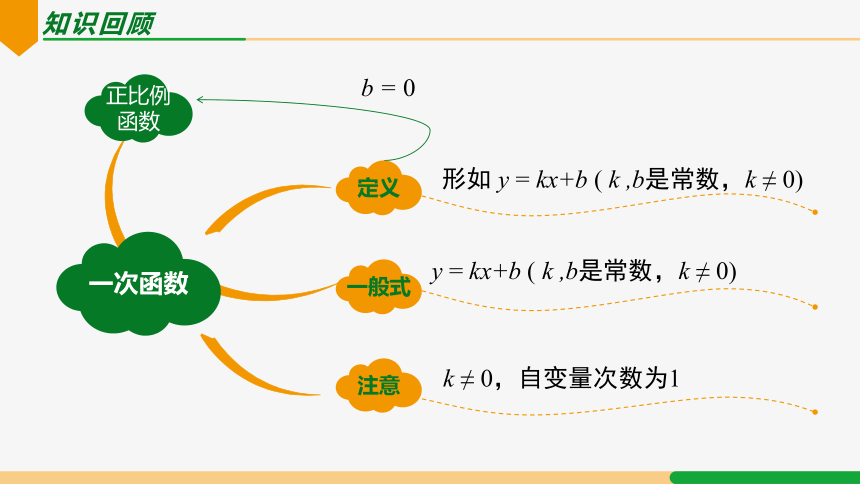
知识回顾
正比例
函数
注意
一般式
一次函数
形如 y = kx+b ( k ,b是常数,k ≠ 0)
y = kx+b ( k ,b是常数,k ≠ 0)
k ≠ 0,自变量次数为1
b = 0
定义
新知探究
问题1 如图,已知一次函数的图象经过 P (0,-1),Q (1,1) 两点.
(1)能确定这个一次函数的解析式吗?说说理由?
(2)若能,怎样确定这个一次函数的解析式
(3)总结一般的求一次函数的解析式的步骤?
知识要点1
待定系数
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
∵ P(0,-1) 和 Q(1,1) 都在该函数图象上,
∴它们的坐标都满足 y = kx + b ,
将这两点坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
k · 0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k = 2,
b = -1.
∴ 这个一次函数的解析式为 y = 2x - 1.
知识要点2
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
典例讲解
例1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
例2. 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
例3. y 与x+2 成正比例,并且当x=4时,y=10,求y 与x 的函数关系式.
解:根据正比例函数的定义,设 y=k (x+2),
∵x=4时,y=10,
∴10=k (4+2),
解得
课堂小结
知识要点1
待定系数
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
知识要点2
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
课堂练习
1.已知正比例函数 y=kx (k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y=-2x
C.y= D.y=-
B
2.若一个正比例函数的图象经过A (3,-6),B (m,-4)两点,则m 的值为( )
A.2 B.8 C.-2 D.-8
A
3.一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3
C.b = 2 D.b = 3
D
y
x
O
2
3
4.若点A(m,n)在一次函数 y=3x+b 的图象上,且3m-n>2,则b的取值范围为( )
A.b>2 B.b>-2
C.b<2 D.b<-2
D
5.已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
设一次函数解析式为y=kx+b.则
解得
所以一次函数解析式为y= x-12.
解:
6.在平面直角坐标系中,一次函数 y=kx+b (k,b 都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当-2<x≤3时,求y 的取值范围;
(2)已知点P (m,n)在该函数的图象上,且m-n=4,求点P 的坐标.
将(1,0),(0,2)代入 y=kx+b
得: 解得:
∴这个函数的解析式为:y=-2x+2.
(1)把x=-2代入 y=-2x+2得,y=6,
把x=3代入 y=-2x+2得,y=-4,
∴y 的取值范围是-4≤y<6.
(2)∵点P (m,n) 在该函数的图象上,∴n=-2m+2.
∵m-n=4,∴m-(-2m+2)=4,
解得m=2. ∴n=-2,∴点P 的坐标为(2,-2).
解:
用待定系数法求一次函数的解析式
19.2.2 一次函数
| 第3课时|
情景引入
怎样求一次函数的解析式?
知识回顾
正比例
函数
注意
一般式
一次函数
形如 y = kx+b ( k ,b是常数,k ≠ 0)
y = kx+b ( k ,b是常数,k ≠ 0)
k ≠ 0,自变量次数为1
b = 0
定义
新知探究
问题1 如图,已知一次函数的图象经过 P (0,-1),Q (1,1) 两点.
(1)能确定这个一次函数的解析式吗?说说理由?
(2)若能,怎样确定这个一次函数的解析式
(3)总结一般的求一次函数的解析式的步骤?
知识要点1
待定系数
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
∵ P(0,-1) 和 Q(1,1) 都在该函数图象上,
∴它们的坐标都满足 y = kx + b ,
将这两点坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
k · 0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k = 2,
b = -1.
∴ 这个一次函数的解析式为 y = 2x - 1.
知识要点2
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
典例讲解
例1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
例2. 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
例3. y 与x+2 成正比例,并且当x=4时,y=10,求y 与x 的函数关系式.
解:根据正比例函数的定义,设 y=k (x+2),
∵x=4时,y=10,
∴10=k (4+2),
解得
课堂小结
知识要点1
待定系数
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
知识要点2
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
课堂练习
1.已知正比例函数 y=kx (k≠0)的图象经过点(1,-2),则这个正比例函数的解析式为( )
A.y=2x B.y=-2x
C.y= D.y=-
B
2.若一个正比例函数的图象经过A (3,-6),B (m,-4)两点,则m 的值为( )
A.2 B.8 C.-2 D.-8
A
3.一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3
C.b = 2 D.b = 3
D
y
x
O
2
3
4.若点A(m,n)在一次函数 y=3x+b 的图象上,且3m-n>2,则b的取值范围为( )
A.b>2 B.b>-2
C.b<2 D.b<-2
D
5.已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
设一次函数解析式为y=kx+b.则
解得
所以一次函数解析式为y= x-12.
解:
6.在平面直角坐标系中,一次函数 y=kx+b (k,b 都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当-2<x≤3时,求y 的取值范围;
(2)已知点P (m,n)在该函数的图象上,且m-n=4,求点P 的坐标.
将(1,0),(0,2)代入 y=kx+b
得: 解得:
∴这个函数的解析式为:y=-2x+2.
(1)把x=-2代入 y=-2x+2得,y=6,
把x=3代入 y=-2x+2得,y=-4,
∴y 的取值范围是-4≤y<6.
(2)∵点P (m,n) 在该函数的图象上,∴n=-2m+2.
∵m-n=4,∴m-(-2m+2)=4,
解得m=2. ∴n=-2,∴点P 的坐标为(2,-2).
解:
