20.1.2 中位数和众数 课件(48张PPT)
文档属性
| 名称 | 20.1.2 中位数和众数 课件(48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 13.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
20.1.2中位数和众数
第20章 数据的分析
教师
xxx
人教版 八年级下册
中位数
数据的集中趋势
众数
01
03
02
CONTANTS
目 录
中位数
01
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.以前通过数据计算,我们学均数,知道它可以反映一组数据的平均水平.这节课我们将在实际问题情境中,进一步探讨平均数的统计意义.
情景引入
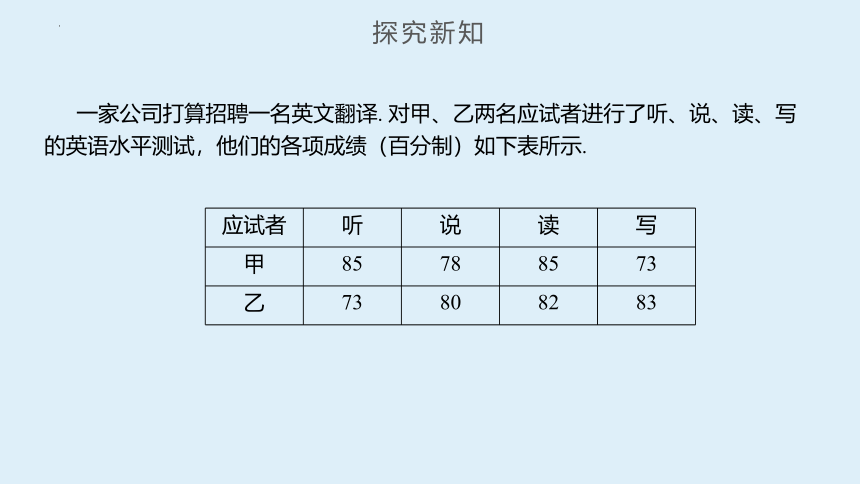
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
探究新知
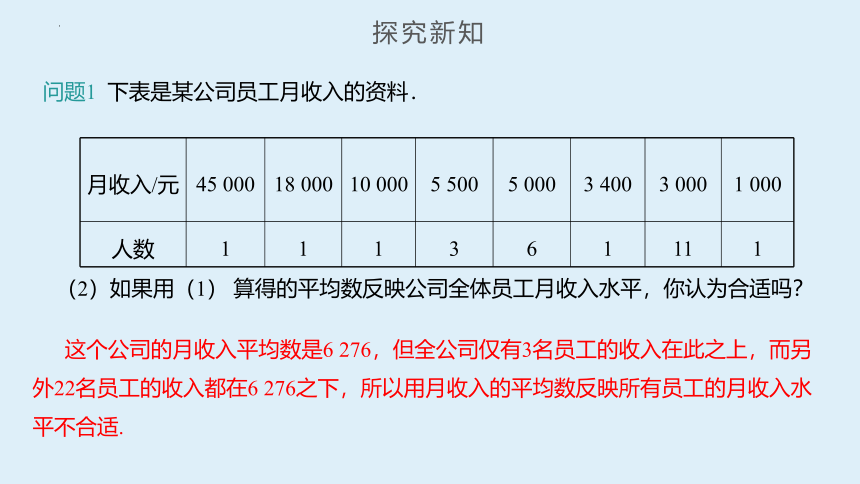
问题1 下表是某公司员工月收入的资料.
(1)计算这个公司员工月收入的平均数.
解:根据表中数据,计算可得这个公司员工月收入的平均数为6 276.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
(2)如果用(1) 算得的平均数反映公司全体员工月收入水平,你认为合适吗?
这个公司的月收入平均数是6 276,但全公司仅有3名员工的收入在此之上,而另外22名员工的收入都在6 276之下,所以用月收入的平均数反映所有员工的月收入水平不合适.
问题1 下表是某公司员工月收入的资料.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
思考:该公司员工的中等收入水平大概是多少元?你是怎样确定的?
“平均数”和“中等水平”谁更合理地反映了该公司绝大部分员工的月工资水平?这个问题中,中等水平的含义是什么?
中等水平比较合理.确定中等收入数值的标准是一半人月工资高于该数值,另一半人月工资低于该数值.
中等水平的含义是中位数,利用中位数可以更好地反映这数据的集中趋势.
探究新知
你能给出中位数的定义吗?
将一组数据按照由小到大(或由大到小)的顺序排列:如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;
如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
探究新知
利用中位数分析数据,可以获得一些信息.例如,将表格中25名员工月收入数据由小到大排列,得到的中位数为3 400,这说明除去月收入为3 400元的员工,一半员工收入高于3 400元,另一半员工收入低于3 400元.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
上述问题中公司员工月收入的平均数为什么会比中位数高得多呢?这说明了什么?
如果一组数据中有极端数据,中位数能比平均数更合理地反映该组数据的整体水平.
探究新知
归纳总结求中位数的步骤.
1.将数据由小到大(或由大到小)排列;
2.数清数据个数是奇数还是偶数,如果数据个数为奇数,则取中间的数作为中位数;如果数据个数为偶数,则取中间两数的平均数作为中位数.
探究新知
例1:在一次男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
典型例题
解:(1)先将样本数据按照由小到大的顺序排列:________________________________
_______________________________
这组数据的中位数 的平均数,
即= .
答:样本数据的中位数是_______.
124 129 136 140 145 146
148 154 158 165 175 180
处于中间的两个数 146, 148
147
典型例题
(2)由(1)知样本数据的中位数为_____,它的意义是:这次马拉松比赛中,大约有______选手的成绩快于147min,有______选手的成绩慢于147min. 这名选手的成绩是142min,快于中位数______ ,因此可以推测他的成绩比_____________选手的成绩好.
147
一半
一半
147
一半以上
典型例题
特别提醒:
一组数据的中位数是唯一的,它可能是这组数据中的某个数,也可能不是这组数据中的数 .
中位数是刻画一组数据的“中等水平”的一个代表,反映了一组数据的集中趋势 .
用中位数作为一组数据的代表,可靠性比较差,因为它不能充分利用所有的数据信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用中位数来描述这组数据的集中趋势.
探究新知
众数
02
思考:下表是某公司员工月收入的资料,如果小张是该公司的一名普通员工,那么你认为他的月工资最有可能是多少元?
如果小李想到该公司应聘一名普通员工岗位,他最关注的是什么信息?
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
关注人数最多的收入是多少元.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
当一组数据有较多的重复数据时,众数往往能更好地反映其集中趋势.在前面的思考中,该公司员工月收入的众数为3 000,这说明公司中收入3 000元的员工人数最多.如果应聘公司的普通员工,这个众数能提供更为有用的信息.
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示. 你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
分析:一般来讲,鞋店比较关心哪种尺码的鞋销售量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数. 一段时间内卖出的30双女鞋的尺码组成一个样本数据,通过分析样本数据可以找出样本数据的众数. 进而可以估计这家鞋店销售哪种尺码的鞋最多.
探究新知
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示. 你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
解:由表可以看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,即23. 5 cm的鞋销售量最大. 因此可以建议鞋店多进23.5 cm的鞋.
探究新知
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数,因为有可能数据出现的频数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
探究新知
特别提醒:
一组数据的众数不一定唯一,可能有一个或几个,也可能没有.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
探究新知
例2 .一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
一般来讲,鞋店比较关心哪种尺码的鞋销售量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数.
典型例题
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
解:由表可看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,即23.5 cm的鞋销售量最大.因此可以建议鞋店多进23.5 cm的鞋.
典型例题
数据的集中趋势
03
平均数、中位数和众数都可以反映一组数据的集中趋势,它们各有自己的特点,能够从不同的角度提供信息.在实际应用中,需要分析问题的情况,选择适当的量反映数据的集中趋势.
下面我们通过实际问题来学习中位数、众数和平均数的综合应用.
探究新知
某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励. 为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
探究新知
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
探究新知
分析:商场服装部统计的每位营业员在某月的销售额组成一个样本,通过分析样本数据的平均数、中位数、众数来估计总体的情况,从而解决问题.
确定一个适当的月销售目标是一个关键问题,如果目标定得太高,多数营业员完不完成任务,会使营业员失去信心;如果目标定得太低,不能发挥营业员的潜力.
探究新知
0
4
2
6
人数
销售额/万元
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
13
14
15
16
17
18
19
22
23
24
26
28
30
32
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:整理题干中所给出的数据,得到如下的表和图.
探究新知
解: (1)从上表或上图可以看出,样本数据的众数是15,中位数是 18, 利用计算器求得这组数据的平均数约是20. 可以推测,这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额大约是20万元.
探究新知
(2)如果想确定一个较高的销售目标,这个目标可以定为每月20万元 (平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最大. 可以估计,月销售额定为每月20万元是一个较高目标,大约会有 的营业员获得奖励.
探究新知
(3)如果想让一半左右的营业员能够达到销售目标,月销售额可以定为每月18万元(中位数). 因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右. 可以估计,如果月销售额定为18万元,将有一半左右的营业员获得奖励.
探究新知
选择具有代表一组数据特点的数据的方法:
对于一组数据,当没有极端值时,用平均数作为这组数据的代表值;当有极端值时,用中位数或众数作为这组数据的代表值.
探究新知
求一组数据的众数的方法:找一组数据的众数,可用观察法;当不易观察时,可用列表的形式把各数据出现的次数全部计算出来,即可得出众数.
探究新知
1.跳远比赛中,所有15位参赛者的成绩互不相同,在已知自己成绩的情况下,要想知道自己是否进入前8名,只需要知道所有参赛者成绩的( )
A、中位数 B、众数
C、平均数 D、加权平均数
A
课堂练习
2.下面两组数据的中位数分别是( )
A.3,3 B.3,4
C.3,4.5 D.4,4.5
(1)5, 6, 2, 3,2
(2)5, 6, 2, 4, 3, 5
C
课堂练习
3.数据8、9、9、8、10、8、9、9、8、10、7、9、 9、8的中位数和众数分别是( )
A.8,8 B.9,9
C.8,9 D.9.10
B
课堂练习
4.一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为( )
A.20 B.21 C.22 D.23
B
课堂练习
5.婷婷的妈妈是一位校鞋经销部的经理,为了解鞋子的销售情况,随机调查了9位学生的鞋子的尺码,由小到大是:
20,21,21,22,22,22,22,23,23
对这组数据的分析中,婷婷的妈妈最感兴趣的数据代表是( )
A.众数 B.平均数 C.中位数
A
课堂练习
6.我校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.众数
C.中位数 D.平均数
C
课堂练习
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8.8
C.8.4,8
D.8.8,8.4
C
课堂练习
8.一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如下表所示:
一般来讲鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据( )
A.平均数 B.众数
C.中位数 D.加权平均数
B
尺码/厘米 23 23.5 24 24.5 25 25.5
销售量/双 5 10 22 39 56 43
课堂练习
9.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,学习委员小兵每周对各小组合作学习的情况进行了综合评分.下表是其中一周的统计数据:这组数据的中位数和众数分别是( )
A.87,88 B.89,90
C.90,90 D.90,91
C
课堂练习
10.如图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是 ( )
A.该学校教职工人数是50人
B.教职工年龄的众数一定在38≤x<40这一组
C.教职工年龄的中位数一定落在40≤x<42这一组
D.年龄在40≤x<42小组的教职工人数占该学校全体教职工总人数的20%
B
课堂练习
如何求一组数据的中位数,众数?
1.求中位数要将一组数据按大小顺序,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序 时,从小到大或从大到小都可以.
2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据, 众数有可能不唯一,注意不要遗漏.
课堂小结
1. 平均数、中位数和众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息.
2. 在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据.
课堂小结
20.1.2中位数和众数
第20章 数据的分析
教师
xxx
人教版 八年级下册
中位数
数据的集中趋势
众数
01
03
02
CONTANTS
目 录
中位数
01
当我们收集到数据后,通常是用统计图表整理和描述数据.为了进一步获取信息,还需要对数据进行分析.以前通过数据计算,我们学均数,知道它可以反映一组数据的平均水平.这节课我们将在实际问题情境中,进一步探讨平均数的统计意义.
情景引入
一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示.
应试者 听 说 读 写
甲 85 78 85 73
乙 73 80 82 83
探究新知
问题1 下表是某公司员工月收入的资料.
(1)计算这个公司员工月收入的平均数.
解:根据表中数据,计算可得这个公司员工月收入的平均数为6 276.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
(2)如果用(1) 算得的平均数反映公司全体员工月收入水平,你认为合适吗?
这个公司的月收入平均数是6 276,但全公司仅有3名员工的收入在此之上,而另外22名员工的收入都在6 276之下,所以用月收入的平均数反映所有员工的月收入水平不合适.
问题1 下表是某公司员工月收入的资料.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
思考:该公司员工的中等收入水平大概是多少元?你是怎样确定的?
“平均数”和“中等水平”谁更合理地反映了该公司绝大部分员工的月工资水平?这个问题中,中等水平的含义是什么?
中等水平比较合理.确定中等收入数值的标准是一半人月工资高于该数值,另一半人月工资低于该数值.
中等水平的含义是中位数,利用中位数可以更好地反映这数据的集中趋势.
探究新知
你能给出中位数的定义吗?
将一组数据按照由小到大(或由大到小)的顺序排列:如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;
如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
探究新知
利用中位数分析数据,可以获得一些信息.例如,将表格中25名员工月收入数据由小到大排列,得到的中位数为3 400,这说明除去月收入为3 400元的员工,一半员工收入高于3 400元,另一半员工收入低于3 400元.
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
探究新知
上述问题中公司员工月收入的平均数为什么会比中位数高得多呢?这说明了什么?
如果一组数据中有极端数据,中位数能比平均数更合理地反映该组数据的整体水平.
探究新知
归纳总结求中位数的步骤.
1.将数据由小到大(或由大到小)排列;
2.数清数据个数是奇数还是偶数,如果数据个数为奇数,则取中间的数作为中位数;如果数据个数为偶数,则取中间两数的平均数作为中位数.
探究新知
例1:在一次男子马拉松长跑比赛中,抽得12名选手所用的时间(单位:min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)一名选手的成绩是142min,他的成绩如何?
典型例题
解:(1)先将样本数据按照由小到大的顺序排列:________________________________
_______________________________
这组数据的中位数 的平均数,
即= .
答:样本数据的中位数是_______.
124 129 136 140 145 146
148 154 158 165 175 180
处于中间的两个数 146, 148
147
典型例题
(2)由(1)知样本数据的中位数为_____,它的意义是:这次马拉松比赛中,大约有______选手的成绩快于147min,有______选手的成绩慢于147min. 这名选手的成绩是142min,快于中位数______ ,因此可以推测他的成绩比_____________选手的成绩好.
147
一半
一半
147
一半以上
典型例题
特别提醒:
一组数据的中位数是唯一的,它可能是这组数据中的某个数,也可能不是这组数据中的数 .
中位数是刻画一组数据的“中等水平”的一个代表,反映了一组数据的集中趋势 .
用中位数作为一组数据的代表,可靠性比较差,因为它不能充分利用所有的数据信息,但它不受极端值的影响,当一组数据中有个别数据变动较大时,可用中位数来描述这组数据的集中趋势.
探究新知
众数
02
思考:下表是某公司员工月收入的资料,如果小张是该公司的一名普通员工,那么你认为他的月工资最有可能是多少元?
如果小李想到该公司应聘一名普通员工岗位,他最关注的是什么信息?
月收入/元 45 000 18 000 10 000 5 500 5 000 3 400 3 000 1 000
人数 1 1 1 3 6 1 11 1
关注人数最多的收入是多少元.
一组数据中出现次数最多的那个数据叫做这组数据的众数.
当一组数据有较多的重复数据时,众数往往能更好地反映其集中趋势.在前面的思考中,该公司员工月收入的众数为3 000,这说明公司中收入3 000元的员工人数最多.如果应聘公司的普通员工,这个众数能提供更为有用的信息.
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示. 你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
分析:一般来讲,鞋店比较关心哪种尺码的鞋销售量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数. 一段时间内卖出的30双女鞋的尺码组成一个样本数据,通过分析样本数据可以找出样本数据的众数. 进而可以估计这家鞋店销售哪种尺码的鞋最多.
探究新知
一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如表所示. 你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
解:由表可以看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,即23. 5 cm的鞋销售量最大. 因此可以建议鞋店多进23.5 cm的鞋.
探究新知
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数,因为有可能数据出现的频数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
探究新知
特别提醒:
一组数据的众数不一定唯一,可能有一个或几个,也可能没有.
众数是一组数据中出现次数最多的数据,而不是数据出现的次数.
探究新知
例2 .一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
一般来讲,鞋店比较关心哪种尺码的鞋销售量最大,也就是关心卖出的鞋的尺码组成的一组数据的众数.
典型例题
例2.一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示.你能根据表中的数据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
解:由表可看出,在鞋的尺码组成的数据中,23.5是这组数据的众数,即23.5 cm的鞋销售量最大.因此可以建议鞋店多进23.5 cm的鞋.
典型例题
数据的集中趋势
03
平均数、中位数和众数都可以反映一组数据的集中趋势,它们各有自己的特点,能够从不同的角度提供信息.在实际应用中,需要分析问题的情况,选择适当的量反映数据的集中趋势.
下面我们通过实际问题来学习中位数、众数和平均数的综合应用.
探究新知
某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励. 为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
探究新知
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
探究新知
分析:商场服装部统计的每位营业员在某月的销售额组成一个样本,通过分析样本数据的平均数、中位数、众数来估计总体的情况,从而解决问题.
确定一个适当的月销售目标是一个关键问题,如果目标定得太高,多数营业员完不完成任务,会使营业员失去信心;如果目标定得太低,不能发挥营业员的潜力.
探究新知
0
4
2
6
人数
销售额/万元
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数
13
14
15
16
17
18
19
22
23
24
26
28
30
32
1
1
5
4
3
2
3
1
1
1
1
2
2
3
解:整理题干中所给出的数据,得到如下的表和图.
探究新知
解: (1)从上表或上图可以看出,样本数据的众数是15,中位数是 18, 利用计算器求得这组数据的平均数约是20. 可以推测,这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额大约是20万元.
探究新知
(2)如果想确定一个较高的销售目标,这个目标可以定为每月20万元 (平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最大. 可以估计,月销售额定为每月20万元是一个较高目标,大约会有 的营业员获得奖励.
探究新知
(3)如果想让一半左右的营业员能够达到销售目标,月销售额可以定为每月18万元(中位数). 因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右. 可以估计,如果月销售额定为18万元,将有一半左右的营业员获得奖励.
探究新知
选择具有代表一组数据特点的数据的方法:
对于一组数据,当没有极端值时,用平均数作为这组数据的代表值;当有极端值时,用中位数或众数作为这组数据的代表值.
探究新知
求一组数据的众数的方法:找一组数据的众数,可用观察法;当不易观察时,可用列表的形式把各数据出现的次数全部计算出来,即可得出众数.
探究新知
1.跳远比赛中,所有15位参赛者的成绩互不相同,在已知自己成绩的情况下,要想知道自己是否进入前8名,只需要知道所有参赛者成绩的( )
A、中位数 B、众数
C、平均数 D、加权平均数
A
课堂练习
2.下面两组数据的中位数分别是( )
A.3,3 B.3,4
C.3,4.5 D.4,4.5
(1)5, 6, 2, 3,2
(2)5, 6, 2, 4, 3, 5
C
课堂练习
3.数据8、9、9、8、10、8、9、9、8、10、7、9、 9、8的中位数和众数分别是( )
A.8,8 B.9,9
C.8,9 D.9.10
B
课堂练习
4.一组数据按从小到大顺序排列为:13、14、19、x、23、27、28、31,其中位数是22,则x为( )
A.20 B.21 C.22 D.23
B
课堂练习
5.婷婷的妈妈是一位校鞋经销部的经理,为了解鞋子的销售情况,随机调查了9位学生的鞋子的尺码,由小到大是:
20,21,21,22,22,22,22,23,23
对这组数据的分析中,婷婷的妈妈最感兴趣的数据代表是( )
A.众数 B.平均数 C.中位数
A
课堂练习
6.我校有25名同学参加某比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的( )
A.最高分 B.众数
C.中位数 D.平均数
C
课堂练习
7.为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8
B.8.4,8.8
C.8.4,8
D.8.8,8.4
C
课堂练习
8.一家鞋店在一段时间内销售了某种男鞋200双,各种尺码鞋的销售量如下表所示:
一般来讲鞋店老板比较关心哪种尺码的鞋最畅销,也就是关心卖出的鞋的尺码组成的一组数据( )
A.平均数 B.众数
C.中位数 D.加权平均数
B
尺码/厘米 23 23.5 24 24.5 25 25.5
销售量/双 5 10 22 39 56 43
课堂练习
9.实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,学习委员小兵每周对各小组合作学习的情况进行了综合评分.下表是其中一周的统计数据:这组数据的中位数和众数分别是( )
A.87,88 B.89,90
C.90,90 D.90,91
C
课堂练习
10.如图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是 ( )
A.该学校教职工人数是50人
B.教职工年龄的众数一定在38≤x<40这一组
C.教职工年龄的中位数一定落在40≤x<42这一组
D.年龄在40≤x<42小组的教职工人数占该学校全体教职工总人数的20%
B
课堂练习
如何求一组数据的中位数,众数?
1.求中位数要将一组数据按大小顺序,顾名思义,中位数就是位置处于最中间的一个数(或最中间的两个数的平均数),排序 时,从小到大或从大到小都可以.
2.众数是一组数据中出现次数最多的数据,是一组数据中的原数据, 众数有可能不唯一,注意不要遗漏.
课堂小结
1. 平均数、中位数和众数都可以作为一组数据的代表,它们各有自己的特点,能够从不同的角度提供信息.
2. 在实际应用中,需要分析具体问题的情况,选择适当的量来代表数据.
课堂小结
