19.2.5 一次函数的解析式的求法 课件(24张PPT)
文档属性
| 名称 | 19.2.5 一次函数的解析式的求法 课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 09:36:45 | ||
图片预览




文档简介
(共24张PPT)
一次函数的解析式的求法
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.(重点、难点)
1.什么叫一次函数?
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
2.一次函数y=kx+b(k,b是常数,k≠0)有什么性质呢?
①当k>0时,y随x的增大而增大;
②当k<0时,y随x的增大而减小.
3.常数k和b是怎样影响函数图象的呢?
①k的正负决定直线的方向.
②b的正负决定直线与y轴交点在原点上方还是下方.
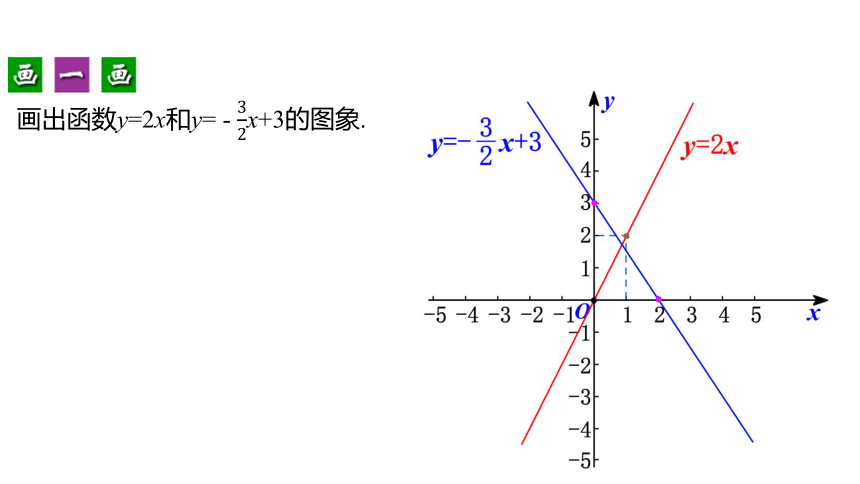
画出函数y=2x和y= - x+3的图象.
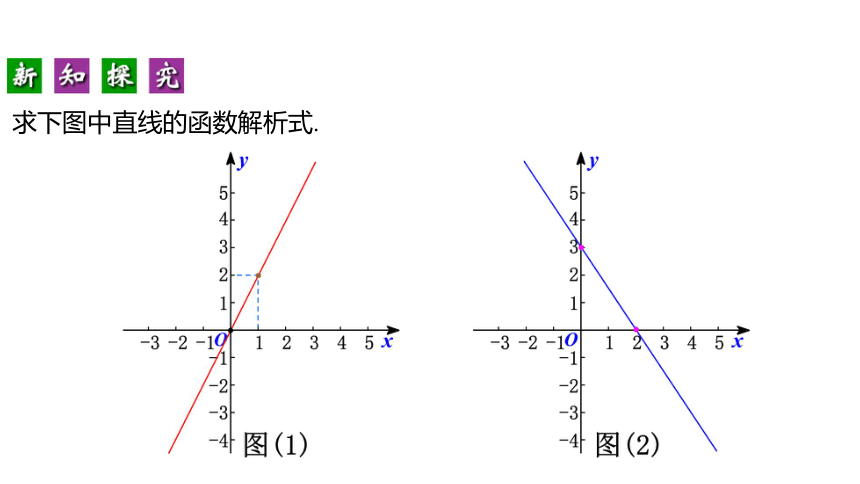
求下图中直线的函数解析式.
求下图中直线的函数解析式.
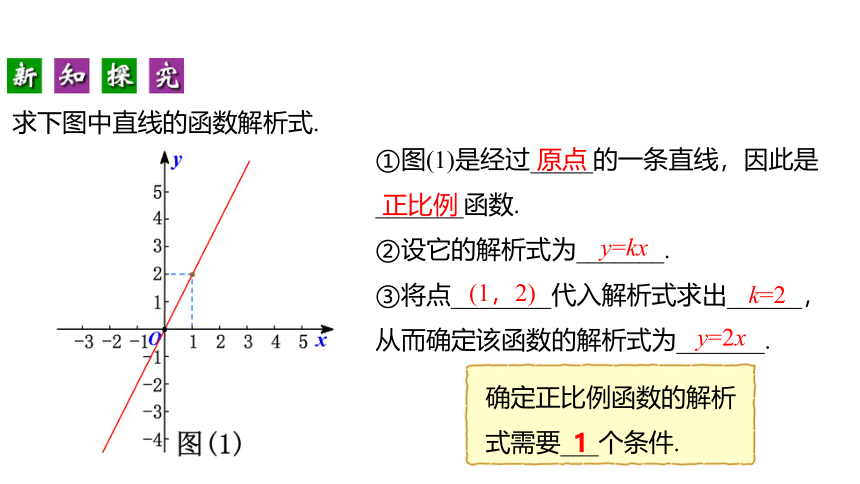
①图(1)是经过_____的一条直线,因此是_______函数.
②设它的解析式为_______.
③将点________代入解析式求出______,从而确定该函数的解析式为_______.
确定正比例函数的解析式需要___个条件.
原点
正比例
y=kx
(1,2)
k=2
y=2x
1
求下图中直线的函数解析式.
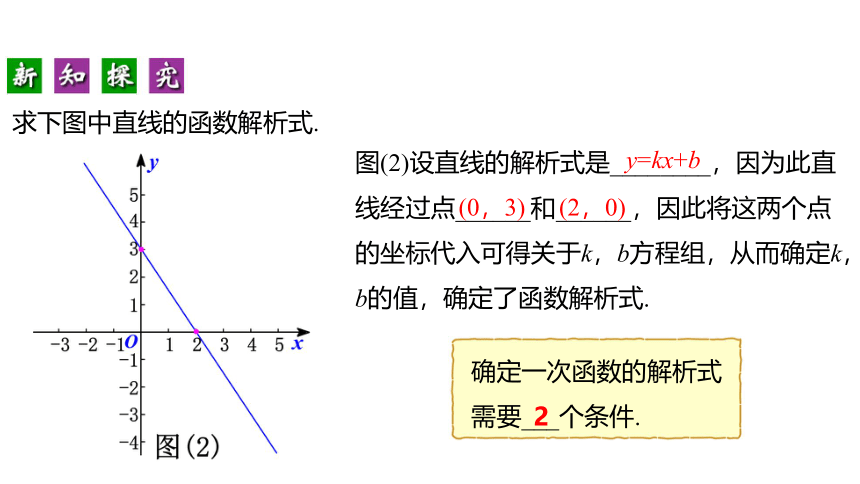
图(2)设直线的解析式是________,因为此直线经过点______和______,因此将这两个点的坐标代入可得关于k,b方程组,从而确定k,b的值,确定了函数解析式.
确定一次函数的解析式需要___个条件.
y=kx+b
(0,3)
(2,0)
2
求下图中直线的函数解析式.
解:设直线的解析式为y=kx+b
∵ 直线经过点(0,3)与(2,0)
∴
解方程组得
∴ 这条直线的解析式为y=-x+3
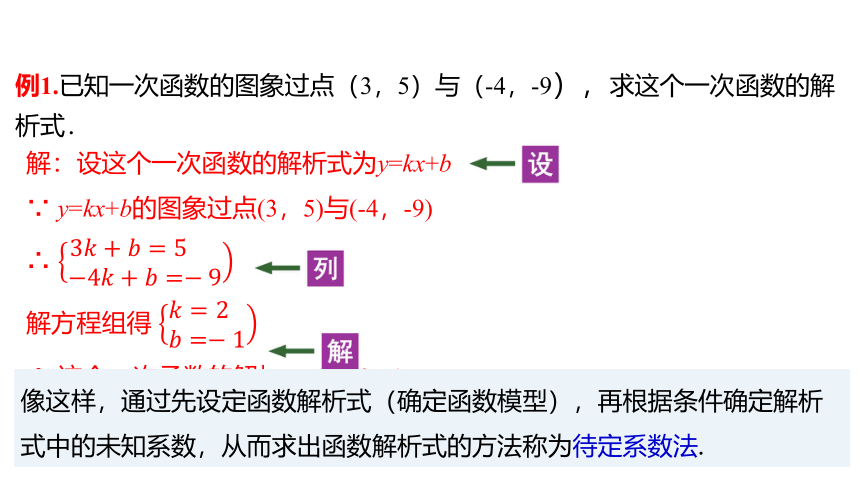
例1.已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(3,5)与(-4,-9)
∴
解方程组得
∴ 这个一次函数的解析式为y=2x-1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
已知一次函数的图象经过点(9,0)和点(24,20),写出函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(9,0)与(24,20)
∴
解方程组得
∴ 这个一次函数的解析式为y=x-12.
例2.若一次函数的图象经过点A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
∵一次函数的图象与直线y=-x+3平行
∴k=-1
把A(2,0)代入y=-x+b中
解得b=2
∴一次函数的解析式为y=-x+2.
例3.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
解:①当k>0时,y随x的增大而增大
∴当x=-3时,y=-5,当x=6时,y=-2.
把这两组值分别代入y=kx+b中
解方程组得
∴一次函数的解析式为y=x-4.
解:②当k<0时,y随x的增大而减小
当x=-3时,y=-2,当x=6时,y=-5
把这两组值分别代入y=kx+b中
得到 解方程组得
∴一次函数的解析式为y=-x-3
综上所述,一次函数的解析式为y=x-4或y=-x-3
例3.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
例4.已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是(- ,0).由题意可列出关于k,b的方程.
x
y
O
2
注意:此题有两种情况.
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是(-,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
典例解析
x
y
O
2
1.一次函数y=kx+b(k≠0)的图象如图,则下列结论正确的是( )
A. k=2 B.k=-3 C. b=2 D. b=-3
2.已知y是x的一次函数,表中列出了部分对应值,则m的值
为( )
A.-1 B.0 C. D.2
D
B
3.若直线y=kx+b经过A(0,2)和B(3, 0)两点,则这个一次函数的解析式是( )
A. y=2x+3 B. y=3x+2 C.y=-x+2 D.y=x-1
4.如图,一次函数的图象经过A,B两点,则这个一次函数的解析式是( )
A.y=x-2 B. y=x-2 C.y=x+2 D. y=x+2
C
A
5.已知一次函数y=kx+b, 当x增加3时,y减小2,则k的值是( )
A.- B.- C. D.
6.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是( )
A.y=-2x-3 B.y=-2x-6 C.y=-2x+3 D.y=-2x+6
A
D
7.已知一次函数y=kx+2, 当x=5时,y=4,则k=_____.
8.若一次函数y=2x+b的图象经过点A(-1,1),则b=____,该函数图象过点B(,____) 和点C(____,0).
9.已知一次函数y=kx+b的图象经过A(4,-5),B(-6,7)两点,则k____0.(填“>”或“<”)
10.一次函数y=mx+|m-1|的图象经过点(0,2),且y随x的增大而增大,则m的值是_____.
11.已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5,则此一-次函数的解析式可能为__________________.
0.4
3
5
-1.5
<
3
y=3x+3或y=-3x+3
12.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且点B的横坐标为1,求直线l对应的函数解析式.
解:设直线l对应的函数解析式为y=kx+b
把x=1代入y=2x, 得y=2
则点B坐标为(1,2)
把(1,2),(0,3)代入y=kx+b
得到 解方程组得
所以直线l对应的函数解析式为y=-x+3
13.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式.
(2)判断点P(-1,1) 是否在这个一次函数的图象上.
(3)求此函数图象与x轴、y轴围成的三角形的面积.
解:(1)设这个一次函数的解析式为y=kx+b
∵y=kx+b的图象过点(-2,-3)与(1, 3)
∴ 解方程组得
∴这个一次函数的解析式为y=2x+1
13.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(2)判断点P(-1,1) 是否在这个一次函数的图象上.
(3)求此函数图象与x轴、y轴围成的三角形的面积.
(2)∵当x=-1时,y=2×(-1)+1≠1
∴点P(-1,1)不在y=2x+1的图象上.
(3)由一次函数的解析式y=2x+1可得,图象与x轴,y轴的交点分别为(-,0),(0,1)
∴此函数图象与x轴、y轴围成的三角形的面积为:××1=
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
一次函数的解析式的求法
1.理解待定系数法的意义.
2.会用待定系数法求一次函数的解析式.(重点、难点)
1.什么叫一次函数?
一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数.当b=0时,y=kx+b就变成了y=kx,所以说正比例函数是一种特殊的一次函数.
2.一次函数y=kx+b(k,b是常数,k≠0)有什么性质呢?
①当k>0时,y随x的增大而增大;
②当k<0时,y随x的增大而减小.
3.常数k和b是怎样影响函数图象的呢?
①k的正负决定直线的方向.
②b的正负决定直线与y轴交点在原点上方还是下方.
画出函数y=2x和y= - x+3的图象.
求下图中直线的函数解析式.
求下图中直线的函数解析式.
①图(1)是经过_____的一条直线,因此是_______函数.
②设它的解析式为_______.
③将点________代入解析式求出______,从而确定该函数的解析式为_______.
确定正比例函数的解析式需要___个条件.
原点
正比例
y=kx
(1,2)
k=2
y=2x
1
求下图中直线的函数解析式.
图(2)设直线的解析式是________,因为此直线经过点______和______,因此将这两个点的坐标代入可得关于k,b方程组,从而确定k,b的值,确定了函数解析式.
确定一次函数的解析式需要___个条件.
y=kx+b
(0,3)
(2,0)
2
求下图中直线的函数解析式.
解:设直线的解析式为y=kx+b
∵ 直线经过点(0,3)与(2,0)
∴
解方程组得
∴ 这条直线的解析式为y=-x+3
例1.已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(3,5)与(-4,-9)
∴
解方程组得
∴ 这个一次函数的解析式为y=2x-1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
已知一次函数的图象经过点(9,0)和点(24,20),写出函数的解析式.
解:设这个一次函数的解析式为y=kx+b
∵ y=kx+b的图象过点(9,0)与(24,20)
∴
解方程组得
∴ 这个一次函数的解析式为y=x-12.
例2.若一次函数的图象经过点A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
∵一次函数的图象与直线y=-x+3平行
∴k=-1
把A(2,0)代入y=-x+b中
解得b=2
∴一次函数的解析式为y=-x+2.
例3.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
解:①当k>0时,y随x的增大而增大
∴当x=-3时,y=-5,当x=6时,y=-2.
把这两组值分别代入y=kx+b中
解方程组得
∴一次函数的解析式为y=x-4.
解:②当k<0时,y随x的增大而减小
当x=-3时,y=-2,当x=6时,y=-5
把这两组值分别代入y=kx+b中
得到 解方程组得
∴一次函数的解析式为y=-x-3
综上所述,一次函数的解析式为y=x-4或y=-x-3
例3.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,求这个函数的解析式.
例4.已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是(- ,0).由题意可列出关于k,b的方程.
x
y
O
2
注意:此题有两种情况.
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是(-,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
典例解析
x
y
O
2
1.一次函数y=kx+b(k≠0)的图象如图,则下列结论正确的是( )
A. k=2 B.k=-3 C. b=2 D. b=-3
2.已知y是x的一次函数,表中列出了部分对应值,则m的值
为( )
A.-1 B.0 C. D.2
D
B
3.若直线y=kx+b经过A(0,2)和B(3, 0)两点,则这个一次函数的解析式是( )
A. y=2x+3 B. y=3x+2 C.y=-x+2 D.y=x-1
4.如图,一次函数的图象经过A,B两点,则这个一次函数的解析式是( )
A.y=x-2 B. y=x-2 C.y=x+2 D. y=x+2
C
A
5.已知一次函数y=kx+b, 当x增加3时,y减小2,则k的值是( )
A.- B.- C. D.
6.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(m,n),且2m+n=6,则直线AB的解析式是( )
A.y=-2x-3 B.y=-2x-6 C.y=-2x+3 D.y=-2x+6
A
D
7.已知一次函数y=kx+2, 当x=5时,y=4,则k=_____.
8.若一次函数y=2x+b的图象经过点A(-1,1),则b=____,该函数图象过点B(,____) 和点C(____,0).
9.已知一次函数y=kx+b的图象经过A(4,-5),B(-6,7)两点,则k____0.(填“>”或“<”)
10.一次函数y=mx+|m-1|的图象经过点(0,2),且y随x的增大而增大,则m的值是_____.
11.已知一次函数y=kx+3的图象与坐标轴围成的三角形的面积是1.5,则此一-次函数的解析式可能为__________________.
0.4
3
5
-1.5
<
3
y=3x+3或y=-3x+3
12.如图,直线l与y轴交于点(0,3),与正比例函数y=2x的图象交于点B,且点B的横坐标为1,求直线l对应的函数解析式.
解:设直线l对应的函数解析式为y=kx+b
把x=1代入y=2x, 得y=2
则点B坐标为(1,2)
把(1,2),(0,3)代入y=kx+b
得到 解方程组得
所以直线l对应的函数解析式为y=-x+3
13.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式.
(2)判断点P(-1,1) 是否在这个一次函数的图象上.
(3)求此函数图象与x轴、y轴围成的三角形的面积.
解:(1)设这个一次函数的解析式为y=kx+b
∵y=kx+b的图象过点(-2,-3)与(1, 3)
∴ 解方程组得
∴这个一次函数的解析式为y=2x+1
13.已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(2)判断点P(-1,1) 是否在这个一次函数的图象上.
(3)求此函数图象与x轴、y轴围成的三角形的面积.
(2)∵当x=-1时,y=2×(-1)+1≠1
∴点P(-1,1)不在y=2x+1的图象上.
(3)由一次函数的解析式y=2x+1可得,图象与x轴,y轴的交点分别为(-,0),(0,1)
∴此函数图象与x轴、y轴围成的三角形的面积为:××1=
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
