7.6余角、补角 课件(28张PPT)
图片预览






文档简介
(共28张PPT)
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第7章 线段与角的画法
7.6余角、补角
操作
1
2
∠1是∠2的余角
∠2是∠1的余角
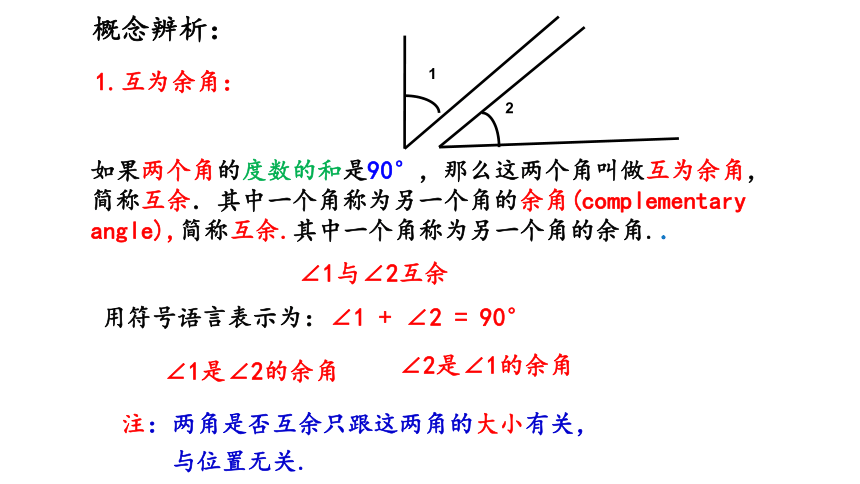
1.互为余角:
概念辨析:
如果两个角的度数的和是90°,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角(complementary angle),简称互余.其中一个角称为另一个角的余角..
∠1与∠2互余
用符号语言表示为:∠1 + ∠2 = 90°
注:两角是否互余只跟这两角的大小有关,
与位置无关.
O
1
2
概念辨析:
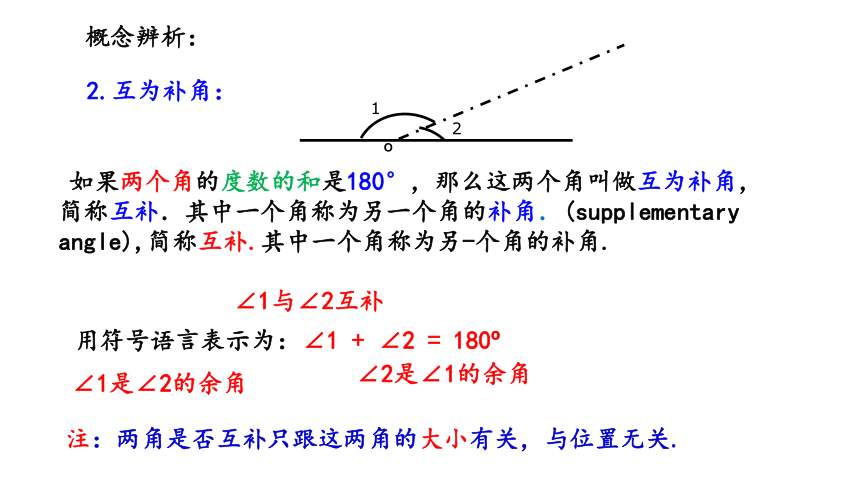
2.互为补角:
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.(supplementary angle),简称互补.其中一个角称为另-个角的补角.
∠1与∠2互补
用符号语言表示为:∠1 + ∠2 = 180
∠1是∠2的余角
∠2是∠1的余角
注:两角是否互补只跟这两角的大小有关,与位置无关.
在研究角的度量时,往往需要比度更小的单位,
90°=89°60 ′
角的度量单位度、分、秒的关系
比如说
180°=179°60 ′
把1度的角分成60等份,那么每1份就是1分,记作1′;
分:
秒:
1分 记作:1′
1秒 记作:1"
再把1分的角分成60等份,每1份就是1秒,记作1″
1°=60′
1′=60"
例题1 已知 =53°38′,求 的余角与补角的度数.
解: 的余角=90°- 53°38′
=126°22′
=36°22′
的补角=180°- 53°38′
例题2、已知一个角的补角是这个角的余角的3倍,求这个角的度数。
解:设这个角为x0
180-x=270-3x
2x=90
x=45
答:这个角为45°
180-x=3(90-x)
1
2
3
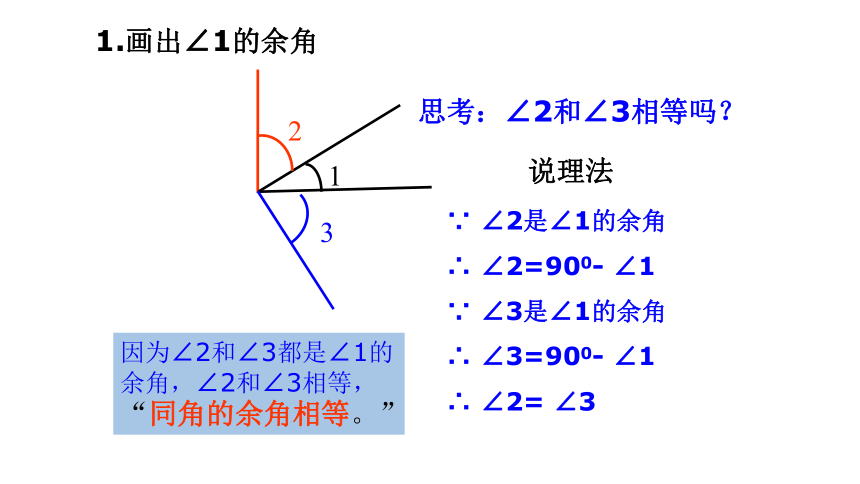
思考:∠2和∠3相等吗?
1.画出∠1的余角
说理法
∵ ∠2是∠1的余角
∴ ∠2=900- ∠1
∵ ∠3是∠1的余角
∴ ∠3=900- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的余角,∠2和∠3相等,
“同角的余角相等。”
2、填空:
⑴35°的余角= _____;
⑵∠α的余角=90°-____;
⑶∠β的余角= ___- ∠β。
当∠α=∠β时,就有∠α的余角和∠β的余角相等,得出“等角的余角相等。”
结合1、2两题结论,得到余角的性质:同角(或等角)的余角相等
550
∠α
90°
当∠α和∠β相等时,∠α的余角和∠β的余角相等吗?
1
2
3
3.画出∠1的补角
思考:∠2和∠3相等吗?
说理法
∵ ∠2是∠1的补角
∴ ∠2=1800- ∠1
∵ ∠3是∠1的补角
∴ ∠3=1800- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的补角,∠2和∠3相等,
“同角的补角相等。”
4.如图∠1与∠2互补, ∠3与∠4互补,如果∠1= ∠3,那么∠2与∠4相等吗?
2
1
3
4
得出结论
“等角的补角相等”。
结合3,4两题的结论,得到补角的性质:
同角(或等角)的补角相等
同角(等角)的余角相等.
同角(等角)的补角相等.
符号语言:
∵∠1 + ∠2 = 90°
∠1 + ∠3 = 90°
∴∠2 =∠3(同角的余角相等)
符号语言:
∵∠1 + ∠2 = 180°
∠1 + ∠3 = 180°
∴∠2 =∠3(同角的补角相等)
归纳性质:
课本练习
1.(1)在下左图中画射线AB,使∠BAC与∠CAD互余
(2)在下右图中画射线AE,使∠EAC与∠CAD互补
2.回答下列问题
(1)一个角与它的余角相等,这个角的度数是多少?
(2)一个角与它的补角相等,这个角的度数是多少?
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
3:计算
(2)89°6′4″-24°27 ′35″
(1)77°54 ′36″+34°27 ′44″
5.已知一个角的补角比它的余角的2倍大35°,求这个角的度数.
随堂检测
2
1
3
1、如图,已知∠1=42°,∠2=138 °,∠3=48°,问图中有没有互余或互补的角?若有,请把它们写出来,并说明理由。
∵ ∠1=42°,∠2=138 °
∴ ∠1+∠2= 42°+138 °=1800
∴ ∠1和∠2互补
解:
A
B
C
D
O
2、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
∵ ∠COD+∠BOD=900
∴ ∠COD和∠BOD互余
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
解:
A
B
C
D
O
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
解:
3、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
A
B
C
D
O
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
4、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
5.填空
的余角 的补角
30°
45°
76°
x°
60°
150°
45°
135°
90°-x°
180°-x°
14°
104°
从这张表格中,比较同一个锐角的余角
和补角的度数,你能发现什么规律?
同一个锐角的补角比它的余角大90度
6.如图,直线CD经过点O,且OC平分∠AOB.
试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
答:∠AOD=∠BOD
又∵∠AOD + ∠AOC =180
∠BOD + ∠BOC =180
∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC =∠BOC
思考题7
A
B
C
D
O
E
(1)图中有几对互余的角,是哪几对?(2)图中有几对相等的角,是哪几对?
(3)图中有几对互补的角,是哪几对?
A
B
C
D
O
E
4对互余的角:
互余
∠AOE与∠COE
∠COD与∠COE
∠COD与∠BOD
∠AOE与∠BOD
A
B
C
D
O
E
5对相等的角:
相等
∠AOC与∠BOC
∠AOC与∠EOD
∠BOC与∠EOD
∠AOE与∠COD
∠EOC与∠BOD
A
B
C
D
O
E
7对互补的角:
互补
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
∠EOD与∠AOC
∠BOE与∠COD
∠EOD与∠BOC
∠AOD与∠EOC
课堂小结:
互为余角(互余) 互为补角(互补)
定义
性质
注意 如果两个角的度数和是90 ,我们就说这两个角互为余角,简称互余.
如果两个角的度数和是180 ,我们就说这两个角互为补角,简称互补.
同角(等角)的余角相等
同角(等角)的补角相等
①互余、互补都是指两个角;
②互余、互补只与两角和有关,
与角的位置无关.
2022-2023学年六年级数学下册同步精品课堂(沪教版)
第7章 线段与角的画法
7.6余角、补角
操作
1
2
∠1是∠2的余角
∠2是∠1的余角
1.互为余角:
概念辨析:
如果两个角的度数的和是90°,那么这两个角叫做互为余角,简称互余.其中一个角称为另一个角的余角(complementary angle),简称互余.其中一个角称为另一个角的余角..
∠1与∠2互余
用符号语言表示为:∠1 + ∠2 = 90°
注:两角是否互余只跟这两角的大小有关,
与位置无关.
O
1
2
概念辨析:
2.互为补角:
如果两个角的度数的和是180°,那么这两个角叫做互为补角,简称互补.其中一个角称为另一个角的补角.(supplementary angle),简称互补.其中一个角称为另-个角的补角.
∠1与∠2互补
用符号语言表示为:∠1 + ∠2 = 180
∠1是∠2的余角
∠2是∠1的余角
注:两角是否互补只跟这两角的大小有关,与位置无关.
在研究角的度量时,往往需要比度更小的单位,
90°=89°60 ′
角的度量单位度、分、秒的关系
比如说
180°=179°60 ′
把1度的角分成60等份,那么每1份就是1分,记作1′;
分:
秒:
1分 记作:1′
1秒 记作:1"
再把1分的角分成60等份,每1份就是1秒,记作1″
1°=60′
1′=60"
例题1 已知 =53°38′,求 的余角与补角的度数.
解: 的余角=90°- 53°38′
=126°22′
=36°22′
的补角=180°- 53°38′
例题2、已知一个角的补角是这个角的余角的3倍,求这个角的度数。
解:设这个角为x0
180-x=270-3x
2x=90
x=45
答:这个角为45°
180-x=3(90-x)
1
2
3
思考:∠2和∠3相等吗?
1.画出∠1的余角
说理法
∵ ∠2是∠1的余角
∴ ∠2=900- ∠1
∵ ∠3是∠1的余角
∴ ∠3=900- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的余角,∠2和∠3相等,
“同角的余角相等。”
2、填空:
⑴35°的余角= _____;
⑵∠α的余角=90°-____;
⑶∠β的余角= ___- ∠β。
当∠α=∠β时,就有∠α的余角和∠β的余角相等,得出“等角的余角相等。”
结合1、2两题结论,得到余角的性质:同角(或等角)的余角相等
550
∠α
90°
当∠α和∠β相等时,∠α的余角和∠β的余角相等吗?
1
2
3
3.画出∠1的补角
思考:∠2和∠3相等吗?
说理法
∵ ∠2是∠1的补角
∴ ∠2=1800- ∠1
∵ ∠3是∠1的补角
∴ ∠3=1800- ∠1
∴ ∠2= ∠3
因为∠2和∠3都是∠1的补角,∠2和∠3相等,
“同角的补角相等。”
4.如图∠1与∠2互补, ∠3与∠4互补,如果∠1= ∠3,那么∠2与∠4相等吗?
2
1
3
4
得出结论
“等角的补角相等”。
结合3,4两题的结论,得到补角的性质:
同角(或等角)的补角相等
同角(等角)的余角相等.
同角(等角)的补角相等.
符号语言:
∵∠1 + ∠2 = 90°
∠1 + ∠3 = 90°
∴∠2 =∠3(同角的余角相等)
符号语言:
∵∠1 + ∠2 = 180°
∠1 + ∠3 = 180°
∴∠2 =∠3(同角的补角相等)
归纳性质:
课本练习
1.(1)在下左图中画射线AB,使∠BAC与∠CAD互余
(2)在下右图中画射线AE,使∠EAC与∠CAD互补
2.回答下列问题
(1)一个角与它的余角相等,这个角的度数是多少?
(2)一个角与它的补角相等,这个角的度数是多少?
(3)互补的两个角能否都是锐角?能否都是直角?能否都是钝角?
3:计算
(2)89°6′4″-24°27 ′35″
(1)77°54 ′36″+34°27 ′44″
5.已知一个角的补角比它的余角的2倍大35°,求这个角的度数.
随堂检测
2
1
3
1、如图,已知∠1=42°,∠2=138 °,∠3=48°,问图中有没有互余或互补的角?若有,请把它们写出来,并说明理由。
∵ ∠1=42°,∠2=138 °
∴ ∠1+∠2= 42°+138 °=1800
∴ ∠1和∠2互补
解:
A
B
C
D
O
2、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
∵ ∠COD+∠BOD=900
∴ ∠COD和∠BOD互余
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
解:
A
B
C
D
O
∵ ∠AOC+∠BOC=1800
∴ ∠AOC和∠BOC互补
解:
3、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
A
B
C
D
O
∵ ∠AOD+∠BOD=1800
∴ ∠AOD和∠BOD互补
4、如图,点O为直线AB上一点,∠AOC是直角,OD是∠BOC内的一条射线,图中有哪些角互补?有哪些角互余?说明你的理由。
解:
5.填空
的余角 的补角
30°
45°
76°
x°
60°
150°
45°
135°
90°-x°
180°-x°
14°
104°
从这张表格中,比较同一个锐角的余角
和补角的度数,你能发现什么规律?
同一个锐角的补角比它的余角大90度
6.如图,直线CD经过点O,且OC平分∠AOB.
试判断∠AOD与∠BOD的大小关系,并说明理由.
O
D
A
B
C
答:∠AOD=∠BOD
又∵∠AOD + ∠AOC =180
∠BOD + ∠BOC =180
∵OC平分∠AOB
∴∠AOD=∠BOD
(等角的补角相等)
∴∠AOC =∠BOC
思考题7
A
B
C
D
O
E
(1)图中有几对互余的角,是哪几对?(2)图中有几对相等的角,是哪几对?
(3)图中有几对互补的角,是哪几对?
A
B
C
D
O
E
4对互余的角:
互余
∠AOE与∠COE
∠COD与∠COE
∠COD与∠BOD
∠AOE与∠BOD
A
B
C
D
O
E
5对相等的角:
相等
∠AOC与∠BOC
∠AOC与∠EOD
∠BOC与∠EOD
∠AOE与∠COD
∠EOC与∠BOD
A
B
C
D
O
E
7对互补的角:
互补
∠AOE与∠BOE
∠AOC与∠BOC
∠AOD与∠BOD
∠EOD与∠AOC
∠BOE与∠COD
∠EOD与∠BOC
∠AOD与∠EOC
课堂小结:
互为余角(互余) 互为补角(互补)
定义
性质
注意 如果两个角的度数和是90 ,我们就说这两个角互为余角,简称互余.
如果两个角的度数和是180 ,我们就说这两个角互为补角,简称互补.
同角(等角)的余角相等
同角(等角)的补角相等
①互余、互补都是指两个角;
②互余、互补只与两角和有关,
与角的位置无关.
