两数和的平方(四川省巴中地区平昌县)
文档属性
| 名称 | 两数和的平方(四川省巴中地区平昌县) |  | |
| 格式 | rar | ||
| 文件大小 | 425.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-09-18 23:53:00 | ||
图片预览





文档简介
课件15张PPT。 坦溪小学 张松柏
2006-12-4两数和的平方§13.3昨天,我们数学老师布置了这样一
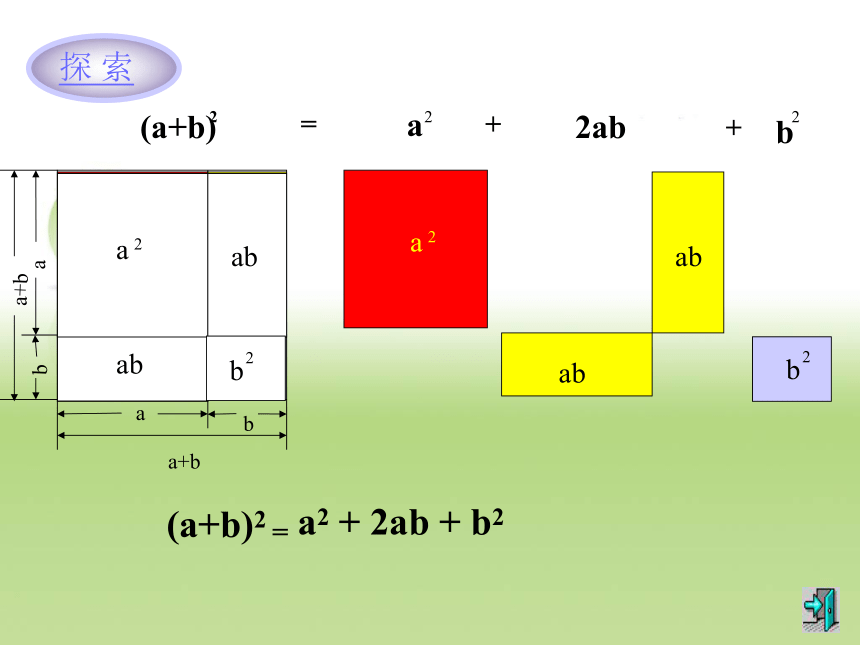
道题目:abab a+bab=+2ab+ 同学们请观察下面等式
左右两边各有什么特征呢?1、左边是两数和的平方,右边可这样记:
“首平方加尾平方,首尾二倍加在中央”两数和的平方公式的特征: (a +b)2=a2+2ab+b2利用两数和的平方公式计算:
(1) (2a+3b)2 (2) (2a+ b)2
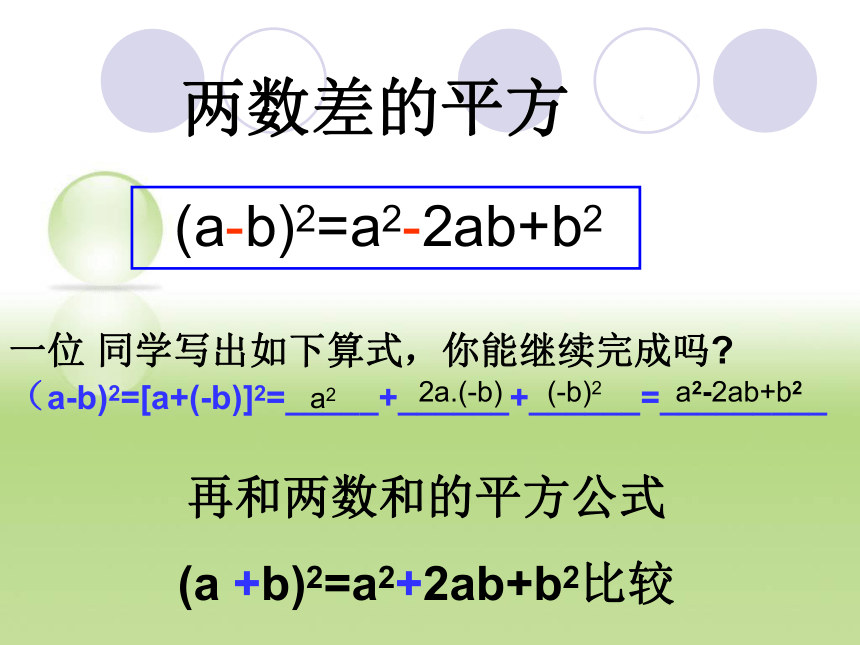
一位 同学写出如下算式,你能继续完成吗?
(a-b)2=[a+(-b)]2=_____+______+______=____________12例题一位 同学写出如下算式,你能继续完成吗? (a-b)2=[a+(-b)]2=_____+______+______=_________a2(-b)22a.(-b)a2-2ab+b2两数差的平方(a-b)2=a2-2ab+b2再和两数和的平方公式
(a +b)2=a2+2ab+b2比较
利用两数差公式计算:
(2a-5b)2
例题1、指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1;
(2) (2a+1)2=4a2 +1;
(3) (?a?1)2=?a2?2a?1.解: (1)第一项被平方时, 未添括号;第一项与第二项乘积的2倍 少乘了一个2 ;应改为: (2a?1)2= (2a)2?2?2a?1+1; (2) 少了第一项与第二项乘积的2倍 (丢了一项);应改为: (2a+1)2= (2a)2+2?2a?1 +1; (3) 第一项平方未添括号, 第一项与第二项乘积的2倍 错了符号;第二项的平方 这一项错了符号;应改为: (?a?1)2=(?a)2?2?(?a )?1+12; 巩固练习巩固练习2、(1) (X+4y)2
(2) ( x- y) 2 1231小组PK现在开始:能力平台展示
请同学们认真学习下面的内容:计算1022 解: 1022
=(100+2)2 =1002+2×100×2+22
=10404仿照上面的方法计算:
(1)632 (2)99.82
?
小结与质疑:
本节课我们共同学习了哪些内容,你有什么心得呢?课堂:教科书 P30 1
课外:用拼图面积说明下列代数式的结果
(1)(a+b+c)2
(2)(a-b)2
同学们 再见
2006-12-4两数和的平方§13.3昨天,我们数学老师布置了这样一
道题目:abab a+bab=+2ab+ 同学们请观察下面等式
左右两边各有什么特征呢?1、左边是两数和的平方,右边可这样记:
“首平方加尾平方,首尾二倍加在中央”两数和的平方公式的特征: (a +b)2=a2+2ab+b2利用两数和的平方公式计算:
(1) (2a+3b)2 (2) (2a+ b)2
一位 同学写出如下算式,你能继续完成吗?
(a-b)2=[a+(-b)]2=_____+______+______=____________12例题一位 同学写出如下算式,你能继续完成吗? (a-b)2=[a+(-b)]2=_____+______+______=_________a2(-b)22a.(-b)a2-2ab+b2两数差的平方(a-b)2=a2-2ab+b2再和两数和的平方公式
(a +b)2=a2+2ab+b2比较
利用两数差公式计算:
(2a-5b)2
例题1、指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1;
(2) (2a+1)2=4a2 +1;
(3) (?a?1)2=?a2?2a?1.解: (1)第一项被平方时, 未添括号;第一项与第二项乘积的2倍 少乘了一个2 ;应改为: (2a?1)2= (2a)2?2?2a?1+1; (2) 少了第一项与第二项乘积的2倍 (丢了一项);应改为: (2a+1)2= (2a)2+2?2a?1 +1; (3) 第一项平方未添括号, 第一项与第二项乘积的2倍 错了符号;第二项的平方 这一项错了符号;应改为: (?a?1)2=(?a)2?2?(?a )?1+12; 巩固练习巩固练习2、(1) (X+4y)2
(2) ( x- y) 2 1231小组PK现在开始:能力平台展示
请同学们认真学习下面的内容:计算1022 解: 1022
=(100+2)2 =1002+2×100×2+22
=10404仿照上面的方法计算:
(1)632 (2)99.82
?
小结与质疑:
本节课我们共同学习了哪些内容,你有什么心得呢?课堂:教科书 P30 1
课外:用拼图面积说明下列代数式的结果
(1)(a+b+c)2
(2)(a-b)2
同学们 再见
