2022-2023学年江苏省盐城市响水二中联盟校高二(下)期中数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年江苏省盐城市响水二中联盟校高二(下)期中数学试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 92.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 09:14:28 | ||
图片预览




文档简介
2022-2023学年江苏省盐城市响水二中联盟校高二(下)期中数学试卷
第I卷(选择题)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的展开式的第项为( )
A. B. C. D.
2. 在展开式中,二项式系数的最大值为 ,含项的系数为,则( )
A. B. C. D.
3. 由,,,四个数组成没有重复数字的四位数中,能被整除的个数是( )
A. B. C. D.
4. 为了提升全民身体素质,学校十分重视学生体育锻炼某校篮球运动员投篮练习,若他第球投进则后一球投进的概率为,若他前一球投不进则后一球投进的概率为若他第球投进的概率为,则他第球投进的概率为( )
A. B. C. D.
5. 在长方体中,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
6. 某药厂用从甲、乙、丙三地收购而来的药材加工生产出一种中成药,三地的供货量分别占,和,且用这三地的药材能生产出优等品的概率分别为,和,则从该厂产品中任意取出一件成品是优等品的概率是( )
A. B. C. D.
7. 已知,则等于( )
A. B. C. D.
8. 已知,是正整数,的展开式中的系数为则展开式中的的系数最小为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 下列利用方向向量、法向量判断线、面位置关系的结论中正确的是( )
A. 若两条不重合直线,的方向向量分别是,则
B. 若直线的方向向量,平面的法向量是,则
C. 若两个不同平面,的法向量分别为,则
D. 若平面经过三点,,,向量是平面的法向量,则
10. 若,,则下列结论中正确的有( )
A.
B.
C.
D.
11. 为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周则( )
A. 某学生从中选门,共有种选法
B. 课程“射”“御”排在不相邻两周,共有种排法
C. 课程“礼”“书”“数”排在相邻三周,共有种排法
D. 课程“乐”不排在第一周,课程“御”不排在最后一周,共有种排法
12. 已知正方体的棱长为,是棱上的一条线段,且,点是棱的中点,是棱上的动点,则下面结论中正确的是( )
A. 与一定不垂直
B. 平面与平面的夹角的正弦值是
C. 的面积是
D. 点到平面的距离是常量
第II卷(非选择题)
三、解答题(本大题共10小题,共90分。解答应写出文字说明,证明过程或演算步骤)
13. 本小题分
,则 ______ .
14. 本小题分
已知空间向量,则向量在向量上的投影向量的坐标是______ .
15. 本小题分
的近似值精确到为______ .
16. 本小题分
东北育才高中部高一年级开设游泳、篮球和足球三门体育选修课,高一某班甲、乙、丙三名同学每人从中只选修一门课程设事件为“甲独自选修一门课程”,为“三人选修的课程都不同”,则概率 ______ .
17. 本小题分
已知的展开式中的第二项和第三项的系数相等.
求的值;
求展开式中所有的有理项.
18. 本小题分
某班有名同学报名参加校运会的四个比赛项目,在下列情况下各有多少种不同的报名方法用数字回答
每人恰好参加一项,每项人数不限;
每项限报一人,且每人至多参加一项;
每人限报一项,人人参加,且每个项目均有人参加.
19. 本小题分
如图,在三棱锥中,平面,,,,,.
Ⅰ求证:平面;
Ⅱ求二面角的余弦值;
Ⅲ求点到平面的距离.
20. 本小题分
用,,,,,这六个数字的部分或全部组成无重复数字的自然数.
在组成的四位数中,求偶数个数;
在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如,等都是“凹数”,试求“凹数”的个数;
在组成的四位数中,若将这些数按从小到大的顺序排成一列,试求第个数字.
21. 本小题分
如图,在四棱台中,底面四边形为菱形,,,平面.
Ⅰ若点是的中点,求证:;
Ⅱ棱上是否存在一点,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
22. 本小题分
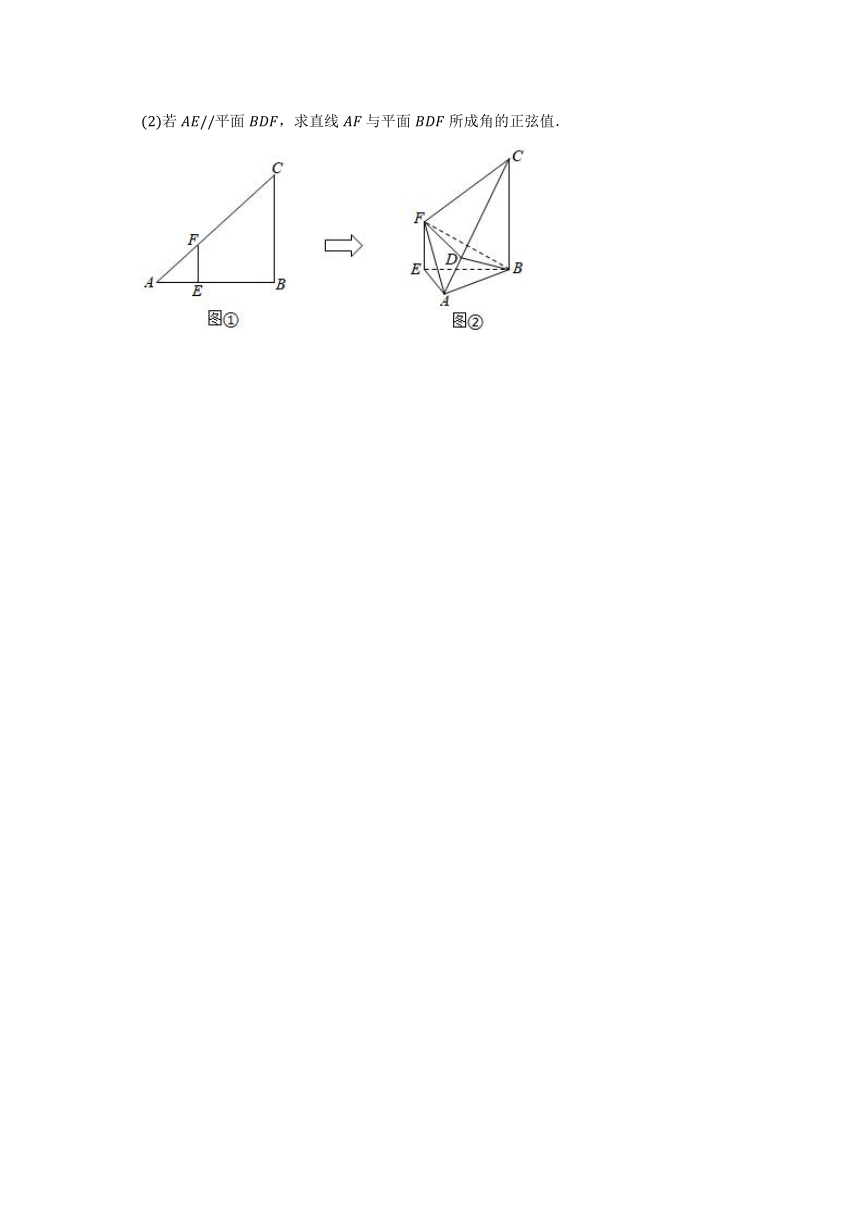
如图,在中,为直角,,,,沿将折起,使,得到如图的几何体,点在线段上.
求证:平面平面;
若平面,求直线与平面所成角的正弦值.
答案和解析
1.【答案】
【解析】解:的展开式的第项为,
故选:.
由题意,利用二项式展开式的通项公式,求出的展开式的第项.
本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.
2.【答案】
【解析】解:在展开式中,二项式系数的最大值为 ,.
展开式中的通项公式:,令,可得.
含项的系数为,
则.
故选:.
在展开式中,二项式系数的最大值为 ,可得展开式中的通项公式:,令,可得,含项的系数.
本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于基础题.
3.【答案】
【解析】解:末位是的有个,末位是的有个,
故能被整除的数共有个,
故选:.
能被整除的四位数末位是或的数,因此分两类,根据分类计数原理计算可得.
本题主要考查了分类计数原理,如何分类时关键,属于基础题.
4.【答案】
【解析】
【分析】
本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
利用相互独立事件概率乘法公式能求出他第球投进的概率.
【解答】
解:某校篮球运动员进行投篮练习,若他前一球投进则后一球投进的概率为,
若他前一球投不进则后一球投进的概率为若他第球投进的概率为,
则他第球投进的概率为:
.
故选B.
5.【答案】
【解析】
【分析】
本题考查异面直线所成角的余弦值的求法,属于基础题.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,利用向量法求出异面直线与所成角的余弦值.
【解答】
解:以为原点,为轴,为轴,为轴,建立空间直角坐标系,
在长方体中,,,
,,,,
,,
设异面直线与所成角为,
则,
异面直线与所成角的余弦值为.
故选C.
6.【答案】
【解析】解:设事件:药材来自甲地,事件:药材来自乙地,事件:药材来自丙地,事件:抽到优等品,
则,,,,,,
所以.
故选:.
利用全概率公式求解即可.
本题主要考查了全概率公式,属于基础题.
7.【答案】
【解析】解:,,
则.
故选:.
由题意利用二项式展开式的通项公式,二项式系数的性质,求得的值.
本题主要考查二项式定理的应用,二项式展开式的通项公式,二项式系数的性质,属于基础题.
8.【答案】
【解析】解:,是正整数,的展开式中的系数为.
展开式中的的系数为,
把代入上式得,的系数为,
故当或时,的系数有最小值为.
故选:.
由的系数为,代入展开式中的的系数为,消元利用二次函数的性质,可得它的最小值.
本题考查了二项式定理、二次函数的性质应用,属于中档题.
9.【答案】
【解析】解:对于,若两条不重合直线,的方向向量分别是,则,则,故A正确,
对于,若直线的方向向量,平面的法向量是,则,则,故B错误,
对于,若两个不同平面,的法向量分别为,则,则,故C正确,
对于,若平面经过三点,,,则,,
又向量是平面的法向量,则,则,故D正确.
故选:.
根据直线方向向量,平面法向量的定义,以及它们与线线平行,线面平行,面面平行,线面垂直的关系可解.
本题考查直线方向向量,平面法向量的定义,以及它们与线线平行,线面平行,面面平行,线面垂直的关系,属于中档题.
10.【答案】
【解析】解:,
对于,令,则,故A正确;
对于,于是,而,故B错误;
对于,令,则,
于是,故C错误;
对于,令,则,
因为,
所以,故D正确.
故选:.
直接根据利用二项式定理将其展开,再结合二项式系数的性质对四个选项依次分析即可求解.
本题主要考查二项式定理的应用,属于基础题.
11.【答案】
【解析】解:根据题意,依次分析选项:
对于,某学生从中选门,门中选门共有种,故A错误;
对于,课程“射”“御”排在不相邻两周,先排好其他的门课程,有个空位可选,在其中任选个,安排“射”“御”,共有种排法,故B错误;
对于,课程“礼”“书”“数”排在相邻三周,由捆绑法分析:将“礼”“书”“数”看成一个整体,与其他门课程全排列,共有种排法,故C正确;
对于,课程“乐”不排在第一周,课程“御”不排在最后一周,分种情况讨论,若课程“乐”排在最后一周,有种排法,若课程“乐”不排在最后一周,
有种排法,则共有种排法,故D正确.
故选:.
根据题意,依次分析选项中计算是否正确,综合即可得答案.
本题考查排列组合的应用,涉及分步、分类计数原理的应用,属于基础题.
12.【答案】
【解析】解:对于,当与点重合时,,故选项A错误;
对于,由于点是棱上的动点,是棱上的一条线段,所以平面即平面,
建立如图所示的空间直角坐标系,则,,,
所以,平面即平面,
设平面的法向量为,
则,即,取,
设平面的法向量为,
则,取,
设二面角为,
所以,
故,故选项B正确;
对于,由于平面,又平面,
所以,所以,所以是的高,
所以,故选项C正确;
对于,由于,且平面,平面,所以平面,
又点在上,所以点到平面的距离为常量,故选项D正确.
故选:.
取特殊位置,当与点重合时,即可判断选项A,建立空间直角坐标系,求出两个平面的法向量,利用向量法求解二面角,即可判断选项B,利用线面垂直的性质定理,可得是的高,利用三角形的面积公式求解即可判断选项C,由线面平行的判定定理判断得到平面,即可判断选项D.
本题以命题的真假为载体考查了线面位置关系、线线位置关系、二面角的求解以及点到面的距离问题,综合性强,考查了逻辑推理能力与空间想象能力,属于中档题.
13.【答案】
【解析】解:由题意,,且,
化简得:,
解得或舍.
故答案为:.
利用排列数公式化简计算即可.
本题考查排列数公式的应用,属于基础题.
14.【答案】
【解析】解:,,
向量在向量上的投影向量的坐标是:.
故答案为:.
根据向量的坐标可求出,然后根据投影向量的计算公式即可求出向量在向量上的投影向量的坐标.
本题考查了向量坐标的数量积运算,投影向量的计算公式,向量坐标的数乘运算,考查了计算能力,属于基础题.
15.【答案】
【解析】解:,
,
,
,
当精确到时,只需取展开式的前三项和为:,则近似值为.
故答案为:.
先将转化为,再结合二项式定理计算即可.
本题主要考查二项式定理的应用,属于基础题.
16.【答案】
【解析】解:根据题意,甲独自选修一门,则有门课程可选,乙,丙只能从剩余的两门课程中选择,事件数为,
三人选修的课程各不相同的事件数,
则.
故答案为:.
根据题意,由排列数公式求出和,由条件概率公式计算可得答案.
本题考查条件概率的计算,涉及排列组合的应用,属于基础题.
17.【答案】解:二项式展开式的通项公式为,;
根据展开式中的第二项和第三项的系数相等,得,即,
解得;
二项式展开式的通项公式为,;
当,,时,对应项是有理项,
所以展开式中所有的有理项为,,.
【解析】通过第二项和第三项的系数相等,求出;
利用通项公式通过的幂指数的取值,求解展开式中所有的有理项.
本题考查二项定理的应用,展开式特定项的求法,是基本知识的考查.
18.【答案】解:根据题意,每人恰好参加一项,每项人数不限,则每人都有种选择,
则有报名方法;
根据题意,每项限报一人,且每人至多参加一项,
在人中任选人,安排其参加四个比赛项目即可,有种报名方法;
根据题意,分步进行分析:
将人分成组,若分为、、、的四组,有种分组方法,
若分为、、、的四组,有种分组方法,
则一共有种分组方法,
将分好的四组安排参加项比赛,有种情况,
则有种报名方法.
【解析】根据题意,每人都有种选择,由分步计数原理计算可得答案;
根据题意,在人中任选人,安排其参加四个比赛项目即可,由排列数公式计算可得答案;
根据题意,分步进行分析:将人分成组,将分好的四组安排参加项比赛,由分步计数原理计算可得答案.
本题考查排列组合的应用,涉及分步计数原理的应用,属于基础题.
19.【答案】解:如图示:
,
以为原点建立空间直角坐标系,
由题意得:,,,,,
Ⅰ证明:,,,
,,
即,,
,
平面;
Ⅱ解:由Ⅰ可得为平面的一个法向量,
设平面的法向量为,
而,,
则,即,
不妨设,可得,
易知二面角为锐角,
因此有,,
即二面角的余弦值是;
Ⅲ解:,,,
作平面,垂足为,
设,且,
由,,得:
,解得,
,,
即点到平面的距离是.
【解析】Ⅰ建立坐标系,求出向量的坐标,得到,,求出线面垂直即可;
Ⅱ设平面的法向量为,求出一个法向量,代入余弦公式即可求出余弦值;
Ⅲ作平面,垂足为,求出的坐标,从而求出点到平面的距离.
本题考查了线面垂直,考查平面的法向量,点到平面的距离,是一道中档题.
20.【答案】解:根据题意,分种情况讨论:
四位偶数的个位为,在其他个数字中,任选个,放在前个数位,有个四位偶数,
四位偶数的个位不是,其个位有种情况,千位有种情况,在其他个数字中,任选个,放在中间个数位,有个四位偶数,
则有个符合题意的四位偶数;
根据题意,先在个数中任意选出个,将最小的数安排在十位,其余个数字安排在百位和个位,
则有个“凹数”,
根据题意,在组成的四位数中,在首位的有个四位数,
在首位,在百位有个四位数,
在首位,在百位有个四位数,
共有个数字,则第个数字为.
【解析】根据题意,按四位偶数的个位数字是否为,分种情况讨论,由加法原理计算可得答案;
根据题意,先在个数中任意选出个,将最小的数安排在十位,其余个数字安排在百位和个位,由分步计数原理计算可得答案;
根据题意,分析在首位和在首位,在百位、在首位,在百位的四位数数目,进而分析可得答案.
本题考查排列组合的应用,涉及分步、分类计数原理的应用,属于基础题.
21.【答案】证明:Ⅰ取中点,连接,是菱形,且,
是正三角形,则,即,
平面,,,
以为坐标原点,分别以,,所在直线为轴,轴,轴,建立空间直角坐标系,
设,
则,,,,
,,
,
,则;
Ⅱ,,,,,,
假设点存在,使得二面角的余弦值为,
设点的坐标为,,,
,
设平面的法向量,
则,取,得,
平面的法向量为,
,,解得:,
又二面角大小为锐角,由图可知,点在线段上,
,即.
【解析】Ⅰ取中点,连接,推导出,,以为坐标原点,分别以,,为轴,轴,轴,建立空间直角坐标系,由向量数量积为证明;
Ⅱ假设点存在,使得二面角的余弦值为,设点的坐标为,,分别求出平面的法向量与平面的法向量,由两法向量所成角的余弦值的绝对值为求解值,可得结论.
本题考查直线与直线垂直的判定,考查空间角的求法求法,训练了空间向量在求解几何问题中的应用,是中档题.
22.【答案】证明:,,,,
又,平面,则,
在中,由,,,
得.
,即,
又,平面,
而平面,则平面平面;
解:以为坐标原点,分别以,所在直线为,轴,
以过垂直于平面的直线为轴建立如图所示空间直角坐标系.
则,,,,.
,,,.
设.
则,
设平面的一个法向量为.
由,取,得.
由平面,得,即.
.
设直线与平面所成角为,
则.
直线与平面所成角的正弦值为.
【解析】由已知平面图形可得,,得到平面,则,求解三角形证明,可得平面,从而得到平面平面;
以为坐标原点,分别以,所在直线为,轴,以过垂直于平面的直线为轴建立如图所示空间直角坐标系.由平面求得平面的一个法向量,再由与所成角的余弦值可得直线与平面所成角的正弦值.
本题考查平面与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.
第I卷(选择题)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1. 的展开式的第项为( )
A. B. C. D.
2. 在展开式中,二项式系数的最大值为 ,含项的系数为,则( )
A. B. C. D.
3. 由,,,四个数组成没有重复数字的四位数中,能被整除的个数是( )
A. B. C. D.
4. 为了提升全民身体素质,学校十分重视学生体育锻炼某校篮球运动员投篮练习,若他第球投进则后一球投进的概率为,若他前一球投不进则后一球投进的概率为若他第球投进的概率为,则他第球投进的概率为( )
A. B. C. D.
5. 在长方体中,,,则异面直线与所成角的余弦值为( )
A. B. C. D.
6. 某药厂用从甲、乙、丙三地收购而来的药材加工生产出一种中成药,三地的供货量分别占,和,且用这三地的药材能生产出优等品的概率分别为,和,则从该厂产品中任意取出一件成品是优等品的概率是( )
A. B. C. D.
7. 已知,则等于( )
A. B. C. D.
8. 已知,是正整数,的展开式中的系数为则展开式中的的系数最小为( )
A. B. C. D.
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9. 下列利用方向向量、法向量判断线、面位置关系的结论中正确的是( )
A. 若两条不重合直线,的方向向量分别是,则
B. 若直线的方向向量,平面的法向量是,则
C. 若两个不同平面,的法向量分别为,则
D. 若平面经过三点,,,向量是平面的法向量,则
10. 若,,则下列结论中正确的有( )
A.
B.
C.
D.
11. 为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周则( )
A. 某学生从中选门,共有种选法
B. 课程“射”“御”排在不相邻两周,共有种排法
C. 课程“礼”“书”“数”排在相邻三周,共有种排法
D. 课程“乐”不排在第一周,课程“御”不排在最后一周,共有种排法
12. 已知正方体的棱长为,是棱上的一条线段,且,点是棱的中点,是棱上的动点,则下面结论中正确的是( )
A. 与一定不垂直
B. 平面与平面的夹角的正弦值是
C. 的面积是
D. 点到平面的距离是常量
第II卷(非选择题)
三、解答题(本大题共10小题,共90分。解答应写出文字说明,证明过程或演算步骤)
13. 本小题分
,则 ______ .
14. 本小题分
已知空间向量,则向量在向量上的投影向量的坐标是______ .
15. 本小题分
的近似值精确到为______ .
16. 本小题分
东北育才高中部高一年级开设游泳、篮球和足球三门体育选修课,高一某班甲、乙、丙三名同学每人从中只选修一门课程设事件为“甲独自选修一门课程”,为“三人选修的课程都不同”,则概率 ______ .
17. 本小题分
已知的展开式中的第二项和第三项的系数相等.
求的值;
求展开式中所有的有理项.
18. 本小题分
某班有名同学报名参加校运会的四个比赛项目,在下列情况下各有多少种不同的报名方法用数字回答
每人恰好参加一项,每项人数不限;
每项限报一人,且每人至多参加一项;
每人限报一项,人人参加,且每个项目均有人参加.
19. 本小题分
如图,在三棱锥中,平面,,,,,.
Ⅰ求证:平面;
Ⅱ求二面角的余弦值;
Ⅲ求点到平面的距离.
20. 本小题分
用,,,,,这六个数字的部分或全部组成无重复数字的自然数.
在组成的四位数中,求偶数个数;
在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如,等都是“凹数”,试求“凹数”的个数;
在组成的四位数中,若将这些数按从小到大的顺序排成一列,试求第个数字.
21. 本小题分
如图,在四棱台中,底面四边形为菱形,,,平面.
Ⅰ若点是的中点,求证:;
Ⅱ棱上是否存在一点,使得二面角的余弦值为?若存在,求线段的长;若不存在,请说明理由.
22. 本小题分
如图,在中,为直角,,,,沿将折起,使,得到如图的几何体,点在线段上.
求证:平面平面;
若平面,求直线与平面所成角的正弦值.
答案和解析
1.【答案】
【解析】解:的展开式的第项为,
故选:.
由题意,利用二项式展开式的通项公式,求出的展开式的第项.
本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.
2.【答案】
【解析】解:在展开式中,二项式系数的最大值为 ,.
展开式中的通项公式:,令,可得.
含项的系数为,
则.
故选:.
在展开式中,二项式系数的最大值为 ,可得展开式中的通项公式:,令,可得,含项的系数.
本题考查了二项式定理的性质及其应用,考查了推理能力与计算能力,属于基础题.
3.【答案】
【解析】解:末位是的有个,末位是的有个,
故能被整除的数共有个,
故选:.
能被整除的四位数末位是或的数,因此分两类,根据分类计数原理计算可得.
本题主要考查了分类计数原理,如何分类时关键,属于基础题.
4.【答案】
【解析】
【分析】
本题考查概率的求法,考查相互独立事件概率乘法公式等基础知识,考查运算求解能力,是基础题.
利用相互独立事件概率乘法公式能求出他第球投进的概率.
【解答】
解:某校篮球运动员进行投篮练习,若他前一球投进则后一球投进的概率为,
若他前一球投不进则后一球投进的概率为若他第球投进的概率为,
则他第球投进的概率为:
.
故选B.
5.【答案】
【解析】
【分析】
本题考查异面直线所成角的余弦值的求法,属于基础题.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,利用向量法求出异面直线与所成角的余弦值.
【解答】
解:以为原点,为轴,为轴,为轴,建立空间直角坐标系,
在长方体中,,,
,,,,
,,
设异面直线与所成角为,
则,
异面直线与所成角的余弦值为.
故选C.
6.【答案】
【解析】解:设事件:药材来自甲地,事件:药材来自乙地,事件:药材来自丙地,事件:抽到优等品,
则,,,,,,
所以.
故选:.
利用全概率公式求解即可.
本题主要考查了全概率公式,属于基础题.
7.【答案】
【解析】解:,,
则.
故选:.
由题意利用二项式展开式的通项公式,二项式系数的性质,求得的值.
本题主要考查二项式定理的应用,二项式展开式的通项公式,二项式系数的性质,属于基础题.
8.【答案】
【解析】解:,是正整数,的展开式中的系数为.
展开式中的的系数为,
把代入上式得,的系数为,
故当或时,的系数有最小值为.
故选:.
由的系数为,代入展开式中的的系数为,消元利用二次函数的性质,可得它的最小值.
本题考查了二项式定理、二次函数的性质应用,属于中档题.
9.【答案】
【解析】解:对于,若两条不重合直线,的方向向量分别是,则,则,故A正确,
对于,若直线的方向向量,平面的法向量是,则,则,故B错误,
对于,若两个不同平面,的法向量分别为,则,则,故C正确,
对于,若平面经过三点,,,则,,
又向量是平面的法向量,则,则,故D正确.
故选:.
根据直线方向向量,平面法向量的定义,以及它们与线线平行,线面平行,面面平行,线面垂直的关系可解.
本题考查直线方向向量,平面法向量的定义,以及它们与线线平行,线面平行,面面平行,线面垂直的关系,属于中档题.
10.【答案】
【解析】解:,
对于,令,则,故A正确;
对于,于是,而,故B错误;
对于,令,则,
于是,故C错误;
对于,令,则,
因为,
所以,故D正确.
故选:.
直接根据利用二项式定理将其展开,再结合二项式系数的性质对四个选项依次分析即可求解.
本题主要考查二项式定理的应用,属于基础题.
11.【答案】
【解析】解:根据题意,依次分析选项:
对于,某学生从中选门,门中选门共有种,故A错误;
对于,课程“射”“御”排在不相邻两周,先排好其他的门课程,有个空位可选,在其中任选个,安排“射”“御”,共有种排法,故B错误;
对于,课程“礼”“书”“数”排在相邻三周,由捆绑法分析:将“礼”“书”“数”看成一个整体,与其他门课程全排列,共有种排法,故C正确;
对于,课程“乐”不排在第一周,课程“御”不排在最后一周,分种情况讨论,若课程“乐”排在最后一周,有种排法,若课程“乐”不排在最后一周,
有种排法,则共有种排法,故D正确.
故选:.
根据题意,依次分析选项中计算是否正确,综合即可得答案.
本题考查排列组合的应用,涉及分步、分类计数原理的应用,属于基础题.
12.【答案】
【解析】解:对于,当与点重合时,,故选项A错误;
对于,由于点是棱上的动点,是棱上的一条线段,所以平面即平面,
建立如图所示的空间直角坐标系,则,,,
所以,平面即平面,
设平面的法向量为,
则,即,取,
设平面的法向量为,
则,取,
设二面角为,
所以,
故,故选项B正确;
对于,由于平面,又平面,
所以,所以,所以是的高,
所以,故选项C正确;
对于,由于,且平面,平面,所以平面,
又点在上,所以点到平面的距离为常量,故选项D正确.
故选:.
取特殊位置,当与点重合时,即可判断选项A,建立空间直角坐标系,求出两个平面的法向量,利用向量法求解二面角,即可判断选项B,利用线面垂直的性质定理,可得是的高,利用三角形的面积公式求解即可判断选项C,由线面平行的判定定理判断得到平面,即可判断选项D.
本题以命题的真假为载体考查了线面位置关系、线线位置关系、二面角的求解以及点到面的距离问题,综合性强,考查了逻辑推理能力与空间想象能力,属于中档题.
13.【答案】
【解析】解:由题意,,且,
化简得:,
解得或舍.
故答案为:.
利用排列数公式化简计算即可.
本题考查排列数公式的应用,属于基础题.
14.【答案】
【解析】解:,,
向量在向量上的投影向量的坐标是:.
故答案为:.
根据向量的坐标可求出,然后根据投影向量的计算公式即可求出向量在向量上的投影向量的坐标.
本题考查了向量坐标的数量积运算,投影向量的计算公式,向量坐标的数乘运算,考查了计算能力,属于基础题.
15.【答案】
【解析】解:,
,
,
,
当精确到时,只需取展开式的前三项和为:,则近似值为.
故答案为:.
先将转化为,再结合二项式定理计算即可.
本题主要考查二项式定理的应用,属于基础题.
16.【答案】
【解析】解:根据题意,甲独自选修一门,则有门课程可选,乙,丙只能从剩余的两门课程中选择,事件数为,
三人选修的课程各不相同的事件数,
则.
故答案为:.
根据题意,由排列数公式求出和,由条件概率公式计算可得答案.
本题考查条件概率的计算,涉及排列组合的应用,属于基础题.
17.【答案】解:二项式展开式的通项公式为,;
根据展开式中的第二项和第三项的系数相等,得,即,
解得;
二项式展开式的通项公式为,;
当,,时,对应项是有理项,
所以展开式中所有的有理项为,,.
【解析】通过第二项和第三项的系数相等,求出;
利用通项公式通过的幂指数的取值,求解展开式中所有的有理项.
本题考查二项定理的应用,展开式特定项的求法,是基本知识的考查.
18.【答案】解:根据题意,每人恰好参加一项,每项人数不限,则每人都有种选择,
则有报名方法;
根据题意,每项限报一人,且每人至多参加一项,
在人中任选人,安排其参加四个比赛项目即可,有种报名方法;
根据题意,分步进行分析:
将人分成组,若分为、、、的四组,有种分组方法,
若分为、、、的四组,有种分组方法,
则一共有种分组方法,
将分好的四组安排参加项比赛,有种情况,
则有种报名方法.
【解析】根据题意,每人都有种选择,由分步计数原理计算可得答案;
根据题意,在人中任选人,安排其参加四个比赛项目即可,由排列数公式计算可得答案;
根据题意,分步进行分析:将人分成组,将分好的四组安排参加项比赛,由分步计数原理计算可得答案.
本题考查排列组合的应用,涉及分步计数原理的应用,属于基础题.
19.【答案】解:如图示:
,
以为原点建立空间直角坐标系,
由题意得:,,,,,
Ⅰ证明:,,,
,,
即,,
,
平面;
Ⅱ解:由Ⅰ可得为平面的一个法向量,
设平面的法向量为,
而,,
则,即,
不妨设,可得,
易知二面角为锐角,
因此有,,
即二面角的余弦值是;
Ⅲ解:,,,
作平面,垂足为,
设,且,
由,,得:
,解得,
,,
即点到平面的距离是.
【解析】Ⅰ建立坐标系,求出向量的坐标,得到,,求出线面垂直即可;
Ⅱ设平面的法向量为,求出一个法向量,代入余弦公式即可求出余弦值;
Ⅲ作平面,垂足为,求出的坐标,从而求出点到平面的距离.
本题考查了线面垂直,考查平面的法向量,点到平面的距离,是一道中档题.
20.【答案】解:根据题意,分种情况讨论:
四位偶数的个位为,在其他个数字中,任选个,放在前个数位,有个四位偶数,
四位偶数的个位不是,其个位有种情况,千位有种情况,在其他个数字中,任选个,放在中间个数位,有个四位偶数,
则有个符合题意的四位偶数;
根据题意,先在个数中任意选出个,将最小的数安排在十位,其余个数字安排在百位和个位,
则有个“凹数”,
根据题意,在组成的四位数中,在首位的有个四位数,
在首位,在百位有个四位数,
在首位,在百位有个四位数,
共有个数字,则第个数字为.
【解析】根据题意,按四位偶数的个位数字是否为,分种情况讨论,由加法原理计算可得答案;
根据题意,先在个数中任意选出个,将最小的数安排在十位,其余个数字安排在百位和个位,由分步计数原理计算可得答案;
根据题意,分析在首位和在首位,在百位、在首位,在百位的四位数数目,进而分析可得答案.
本题考查排列组合的应用,涉及分步、分类计数原理的应用,属于基础题.
21.【答案】证明:Ⅰ取中点,连接,是菱形,且,
是正三角形,则,即,
平面,,,
以为坐标原点,分别以,,所在直线为轴,轴,轴,建立空间直角坐标系,
设,
则,,,,
,,
,
,则;
Ⅱ,,,,,,
假设点存在,使得二面角的余弦值为,
设点的坐标为,,,
,
设平面的法向量,
则,取,得,
平面的法向量为,
,,解得:,
又二面角大小为锐角,由图可知,点在线段上,
,即.
【解析】Ⅰ取中点,连接,推导出,,以为坐标原点,分别以,,为轴,轴,轴,建立空间直角坐标系,由向量数量积为证明;
Ⅱ假设点存在,使得二面角的余弦值为,设点的坐标为,,分别求出平面的法向量与平面的法向量,由两法向量所成角的余弦值的绝对值为求解值,可得结论.
本题考查直线与直线垂直的判定,考查空间角的求法求法,训练了空间向量在求解几何问题中的应用,是中档题.
22.【答案】证明:,,,,
又,平面,则,
在中,由,,,
得.
,即,
又,平面,
而平面,则平面平面;
解:以为坐标原点,分别以,所在直线为,轴,
以过垂直于平面的直线为轴建立如图所示空间直角坐标系.
则,,,,.
,,,.
设.
则,
设平面的一个法向量为.
由,取,得.
由平面,得,即.
.
设直线与平面所成角为,
则.
直线与平面所成角的正弦值为.
【解析】由已知平面图形可得,,得到平面,则,求解三角形证明,可得平面,从而得到平面平面;
以为坐标原点,分别以,所在直线为,轴,以过垂直于平面的直线为轴建立如图所示空间直角坐标系.由平面求得平面的一个法向量,再由与所成角的余弦值可得直线与平面所成角的正弦值.
本题考查平面与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.
同课章节目录
