正弦定理
图片预览




文档简介
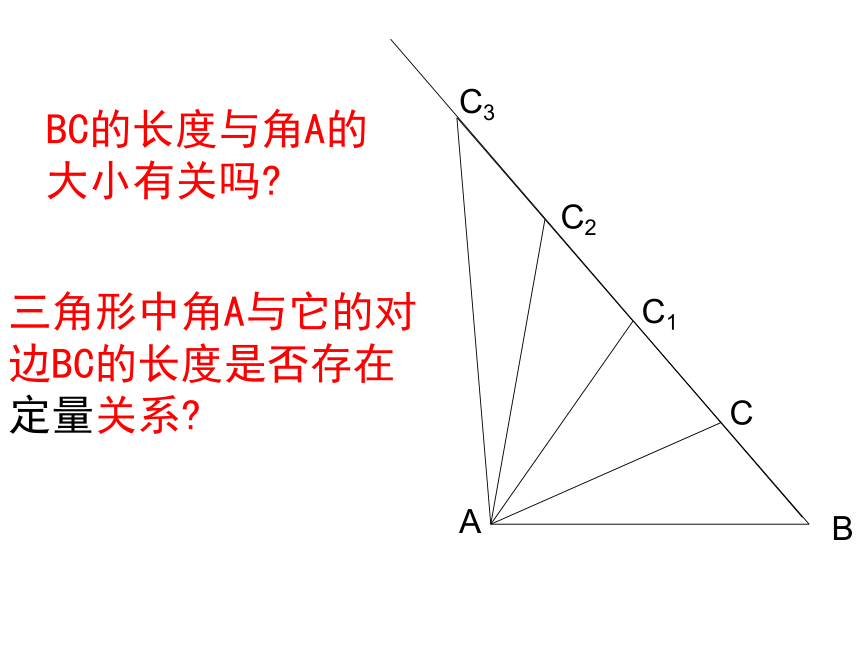
课件18张PPT。正弦定理学科网ABBC的长度与角A的大小有关吗?三角形中角A与它的对边BC的长度是否存在定量关系?在Rt△ABC中,各角与其对边的关系:
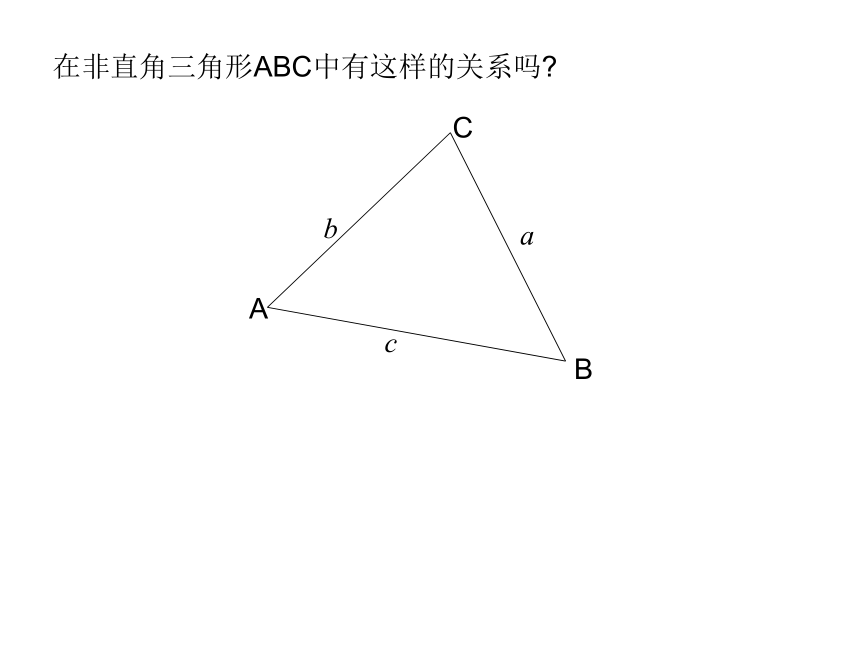
不难得到:CBAabc在非直角三角形ABC中有这样的关系吗?正弦定理:在一个三角形中,各边和它所对角的
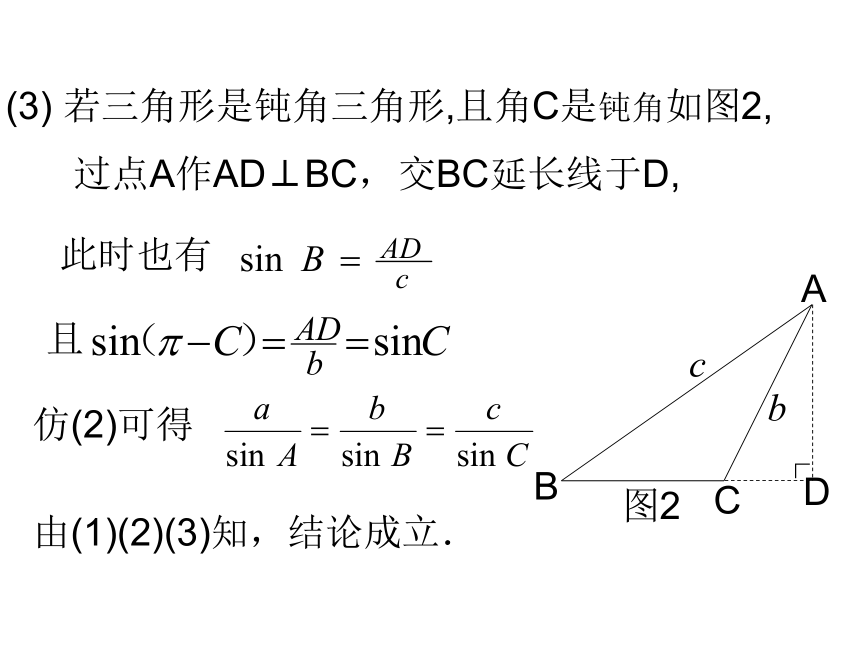
正弦的比相等.即(1) 若直角三角形,已证得结论成立.所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 证法1:(2)若三角形是锐角三角形, 如图1,学科网由(1)(2)(3)知,结论成立.且仿(2)可得(3) 若三角形是钝角三角形,且角C是钝角如图2, 此时也有交BC延长线于D,过点A作AD⊥BC,(2R为△ABC外接圆直径)=2R思考求证:证明:作外接圆O,过B作直径BC/,连AC/,剖析定理、加深理解正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b.解: 且 ∵19.32=已知两角和任意边,
求其他两边和一角∵14.14=a在△ABC中,已知 A=75°,B= 45°,c=
求a , b.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.[a= ,c= ]练习例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
的对角,求其他边和角解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.[B=90°,C=60°,c= ](2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解课堂小结(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考
不难得到:CBAabc在非直角三角形ABC中有这样的关系吗?正弦定理:在一个三角形中,各边和它所对角的
正弦的比相等.即(1) 若直角三角形,已证得结论成立.所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 证法1:(2)若三角形是锐角三角形, 如图1,学科网由(1)(2)(3)知,结论成立.且仿(2)可得(3) 若三角形是钝角三角形,且角C是钝角如图2, 此时也有交BC延长线于D,过点A作AD⊥BC,(2R为△ABC外接圆直径)=2R思考求证:证明:作外接圆O,过B作直径BC/,连AC/,剖析定理、加深理解正弦定理可以解决三角形中哪类问题:① 已知两角和一边,求其他角和边. ②
已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角.定理的应用例 1在△ABC 中,已知c = 10,A = 45。, C = 30。求 a , b.解: 且 ∵19.32=已知两角和任意边,
求其他两边和一角∵14.14=a在△ABC中,已知 A=75°,B= 45°,c=
求a , b.在△ABC中,已知 A=30°,B=120°,b=12
求a , c.[a= ,c= ]练习例 2 已知a=16, b= , A=30° .
求角B,C和边c已知两边和其中一边
的对角,求其他边和角解:由正弦定理得所以B=60°,或B=120°C=90°C=30°当B=120°时变式: a=30, b=26, A=30°求角B,C和边c
由于154.30 +300>1800故B只有一解 (如图)C=124.30,变式: a=30, b=26, A=30°求角B,C和边c
所以B=25.70,C=124.30,∵a > b ∴ A > B ,三角形中大边对大角已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形 (1)b=13,a=26,B=30°.[B=90°,C=60°,c= ](2) b=40,c=20,C=45°.练习注:三角形中角的正弦值小于1时,角可能有两解无解课堂小结(1)三角形常用公式:(2)正弦定理应用范围:① 已知两角和任意边,求其他两边和一角 ②
已知两边和其中一边的对角,求另一边
的对角。(注意解的情况)正弦定理:已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考
