河北省唐山市乐亭县2022-2023学年冀教版七年级下学期期中数学试卷(含答案)
文档属性
| 名称 | 河北省唐山市乐亭县2022-2023学年冀教版七年级下学期期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 15:21:00 | ||
图片预览

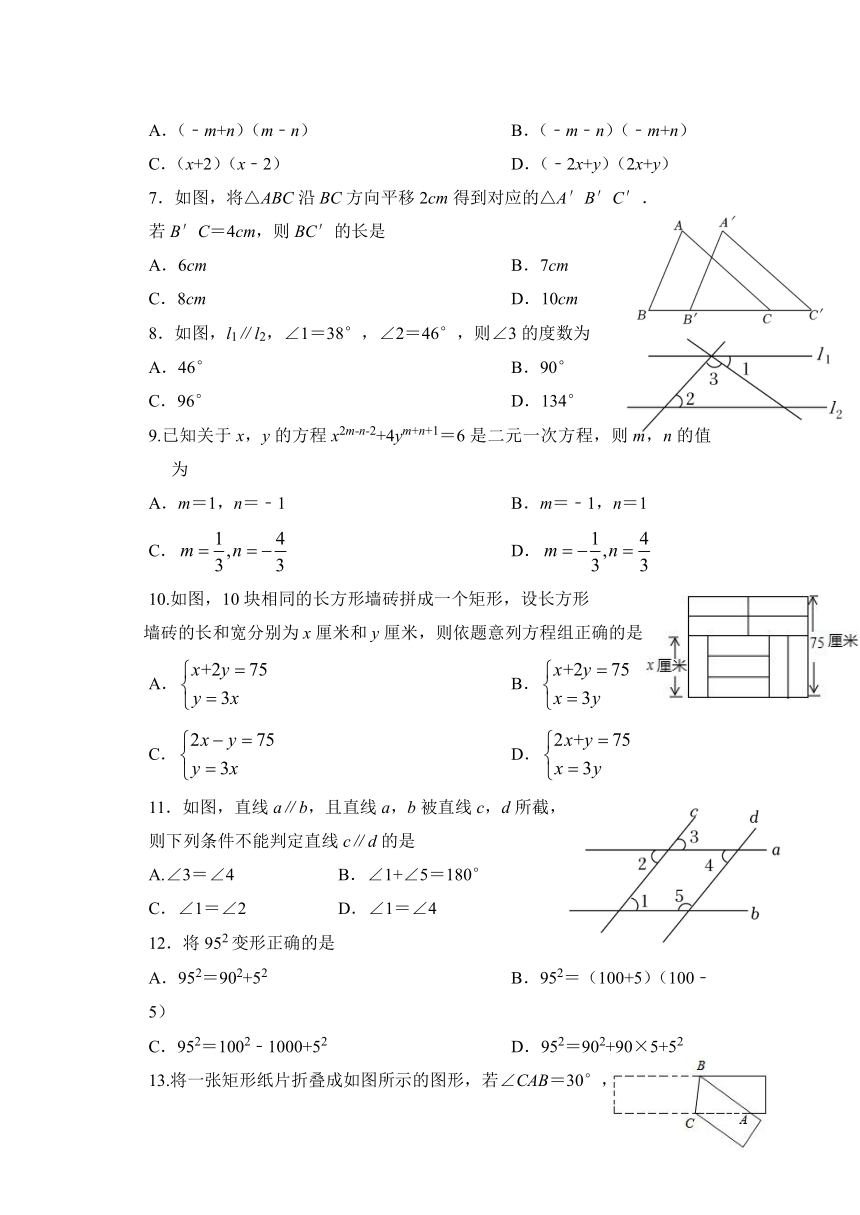

文档简介
2022—2023学年度第二学期期中质量检测
七年级数学试卷
题号 一 二 21 22 23 24 25 26 总分
得分
温馨提示:
1.本试题满分120分。考试时间90分钟。
2.答卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。
3.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。答在试卷上无效。
得分 评卷人 一、用心选一选(每小题3分,共48分,每个小题给出的四个选项中,只有一个选项符合题意)
1.计算a2 a3的结果是
A.a2 B.a3 C.a5 D.a6
2.若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为
A.﹣5 B.﹣1 C.2 D.7
3.全国共有城市新能源公交车46.61万辆,将46.61万用科学记数法表示为4.661×10n,则n等于
A.6 B.5 C.4 D.3
4.下列计算正确的是
A.(a2b)2=a2b2 B.a6÷a2=a3
C.(3xy2)2=6x2y4 D.(﹣m)7÷(﹣m)2=﹣m5
5.已知方程组,则x﹣y的值为
A. B.2 C.3 D.﹣2
6.下列不能用平方差公式直接计算的是
A.(﹣m+n)(m﹣n) B.(﹣m﹣n)(﹣m+n)
C.(x+2)(x﹣2) D.(﹣2x+y)(2x+y)
7.如图,将△ABC沿BC方向平移2cm得到对应的△A′B′C′.
若B′C=4cm,则BC′的长是
A.6cm B.7cm
C.8cm D.10cm
8.如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为
A.46° B.90°
C.96° D.134°
9.已知关于x,y的方程x2m-n-2+4ym+n+1=6是二元一次方程,则m,n的值为
A.m=1,n=﹣1 B.m=﹣1,n=1
C. D.
10.如图,10块相同的长方形墙砖拼成一个矩形,设长方形
墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是
A. B.
C. D.
11.如图,直线a∥b,且直线a,b被直线c,d所截,
则下列条件不能判定直线c∥d的是
A.∠3=∠4 B.∠1+∠5=180°
C.∠1=∠2 D.∠1=∠4
12.将952变形正确的是
A.952=902+52 B.952=(100+5)(100﹣5)
C.952=1002﹣1000+52 D.952=902+90×5+52
13.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,
则∠ACB的度数是
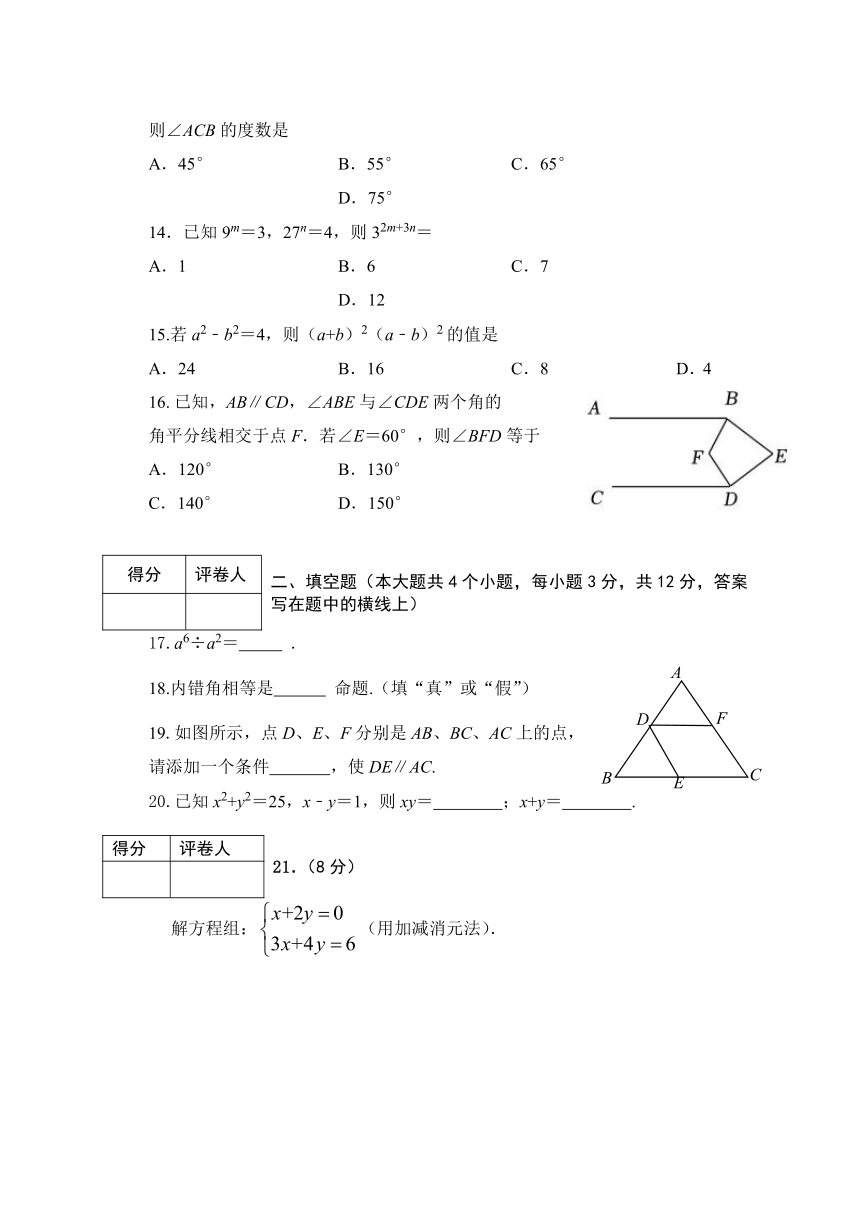
A.45° B.55° C.65° D.75°
14.已知9m=3,27n=4,则32m+3n=
A.1 B.6 C.7 D.12
15.若a2﹣b2=4,则(a+b)2(a﹣b)2的值是
A.24 B.16 C.8 D.4
已知,AB∥CD,∠ABE与∠CDE两个角的
角平分线相交于点F.若∠E=60°,则∠BFD等于
A.120° B.130°
C.140° D.150°
得分 评卷人 二、填空题(本大题共4个小题,每小题3分,共12分,答案写在题中的横线上)
(
B
A
C
E
D
F
)17.a6÷a2= .
18.内错角相等是 命题.(填“真”或“假”)
19.如图所示,点D、E、F分别是AB、BC、AC上的点,
请添加一个条件 ,使DE∥AC.
20.已知x2+y2=25,x﹣y=1,则xy= ;x+y= .
得分 评卷人 21.(8分)
解方程组:(用加减消元法).
得分 评卷人 22.(本题8分)
先化简,再求值:(1+x)(1﹣x)+x(x+2),其中x=.
得分 评卷人 23.(本题10分)
如图,在直角三角形ABC中,∠C=90°,BC=4cm,AC=3cm.
(1)点B到AC的距离是 cm;点A到BC的距是 cm.
(2)画出表示点C到AB的距离的垂线段CD.
(3)AC CD(填“>”“<”“=”),
理由是 .
得分 评卷人 24.(本题11分)
如图,已知∠1=48°,∠2=132°,∠C=∠D.求证:
(1)BD∥CE;
(2)∠A=∠F.
得分 评卷人 25.(本题11分)
发现 :两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和.
(1)验证 :如,(2+1)2+(2﹣1)2=10为偶数.请把10的一半表示为两个正整数的平方和;
(2)探究:设“发现”中的两个已知正整数为m,n,请论证“发现”中的结论正确.
(3)延伸:两个相邻奇数的平方差一定是8的倍数,这个命题是 命题(填“真或假”)
得分 评卷人 26.(本题12分)
某公司购买了一批物资.调查得知,2辆小货车与3辆大货车一次可以满载运输1800件;3辆小货车与4辆大货车一次可以满载运输2500件.
(1)求1辆大货车和1辆小货车一次可以分别满载运输多少件物资?
(2)现有3100件物资需要运往唐山,准备同时租用这两种货车,每辆均全部装满货
物,有几种租车方案?请写出所有租车方案.
七年级数学答案
一、1-5CDBDC 6-10ACCAB 11-16 CCDDBD
二、17. a4 18.假 19.合理即可 20. 12,
21. 解:
①×2得2 x+4 y=0③……………2分
②﹣③得:
x=6…………………4分
把x=6带入①中
解得:y=﹣3………………6分
所以原方程组的解为:.…………………8分
22. 解:(1+x)(1﹣x)+x(x+2)
=1﹣x2+x2+2x……………..4分(对一项得1分)
=1+2x…………6分
当x=时,原式=1+=1+1=2.……………8分
23. 解:(1)4,3.………………4分
(2)图略:……………6分
(3)>…………8分
垂线段最短…………….10分
24. 证明:(1)∵∠1=48°,∠2=132°,
∴∠1+∠2=180°…………2分
∴BD∥CE;………………5分
(2)∵BD∥CE,
∴∠C=∠ABD……………7分
又∵∠C=∠D,
∴∠ABD=∠D…………9分
∴AC∥DF…………10分
∴∠A=∠F……………11分
25. 解:验证:10的一半为5,
5=1+4=12+22………………3分
(m+n)2+(m﹣n)2
=m2+2mn+n2+m2﹣2mn+n2………………6分
=2m2+2n2………………7分
=2(m2+n2)……………8分
故两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和…………9分
(3)真………………11分
26. 解:(1)设1辆小货车一次可满载运输x件物资,1辆大货车一次可满载运输y件物资
由题意可得:…………………5分
解得:……………………8分
答:1辆小货车一次可以满载运输300件物资,1辆大货车一次可以满载运输400件物资.
(2)解:设租用小货车a辆,大货车b辆,
依题意得:300a+400b=3100……………9分
∴.
又∵a,b均为正整数,
∴或或,
∴共有3种租车方案,方案1:租用9辆小货车,1辆大货车;
方案2:租用5辆小货车,4辆大货车;
方案3:租用1辆小货车,7辆大货车.…………………12分(写对一个方案得1分)
七年级数学试卷
题号 一 二 21 22 23 24 25 26 总分
得分
温馨提示:
1.本试题满分120分。考试时间90分钟。
2.答卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。
3.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。答在试卷上无效。
得分 评卷人 一、用心选一选(每小题3分,共48分,每个小题给出的四个选项中,只有一个选项符合题意)
1.计算a2 a3的结果是
A.a2 B.a3 C.a5 D.a6
2.若是关于x、y的二元一次方程ax﹣3y=1的解,则a的值为
A.﹣5 B.﹣1 C.2 D.7
3.全国共有城市新能源公交车46.61万辆,将46.61万用科学记数法表示为4.661×10n,则n等于
A.6 B.5 C.4 D.3
4.下列计算正确的是
A.(a2b)2=a2b2 B.a6÷a2=a3
C.(3xy2)2=6x2y4 D.(﹣m)7÷(﹣m)2=﹣m5
5.已知方程组,则x﹣y的值为
A. B.2 C.3 D.﹣2
6.下列不能用平方差公式直接计算的是
A.(﹣m+n)(m﹣n) B.(﹣m﹣n)(﹣m+n)
C.(x+2)(x﹣2) D.(﹣2x+y)(2x+y)
7.如图,将△ABC沿BC方向平移2cm得到对应的△A′B′C′.
若B′C=4cm,则BC′的长是
A.6cm B.7cm
C.8cm D.10cm
8.如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为
A.46° B.90°
C.96° D.134°
9.已知关于x,y的方程x2m-n-2+4ym+n+1=6是二元一次方程,则m,n的值为
A.m=1,n=﹣1 B.m=﹣1,n=1
C. D.
10.如图,10块相同的长方形墙砖拼成一个矩形,设长方形
墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是
A. B.
C. D.
11.如图,直线a∥b,且直线a,b被直线c,d所截,
则下列条件不能判定直线c∥d的是
A.∠3=∠4 B.∠1+∠5=180°
C.∠1=∠2 D.∠1=∠4
12.将952变形正确的是
A.952=902+52 B.952=(100+5)(100﹣5)
C.952=1002﹣1000+52 D.952=902+90×5+52
13.将一张矩形纸片折叠成如图所示的图形,若∠CAB=30°,
则∠ACB的度数是
A.45° B.55° C.65° D.75°
14.已知9m=3,27n=4,则32m+3n=
A.1 B.6 C.7 D.12
15.若a2﹣b2=4,则(a+b)2(a﹣b)2的值是
A.24 B.16 C.8 D.4
已知,AB∥CD,∠ABE与∠CDE两个角的
角平分线相交于点F.若∠E=60°,则∠BFD等于
A.120° B.130°
C.140° D.150°
得分 评卷人 二、填空题(本大题共4个小题,每小题3分,共12分,答案写在题中的横线上)
(
B
A
C
E
D
F
)17.a6÷a2= .
18.内错角相等是 命题.(填“真”或“假”)
19.如图所示,点D、E、F分别是AB、BC、AC上的点,
请添加一个条件 ,使DE∥AC.
20.已知x2+y2=25,x﹣y=1,则xy= ;x+y= .
得分 评卷人 21.(8分)
解方程组:(用加减消元法).
得分 评卷人 22.(本题8分)
先化简,再求值:(1+x)(1﹣x)+x(x+2),其中x=.
得分 评卷人 23.(本题10分)
如图,在直角三角形ABC中,∠C=90°,BC=4cm,AC=3cm.
(1)点B到AC的距离是 cm;点A到BC的距是 cm.
(2)画出表示点C到AB的距离的垂线段CD.
(3)AC CD(填“>”“<”“=”),
理由是 .
得分 评卷人 24.(本题11分)
如图,已知∠1=48°,∠2=132°,∠C=∠D.求证:
(1)BD∥CE;
(2)∠A=∠F.
得分 评卷人 25.(本题11分)
发现 :两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和.
(1)验证 :如,(2+1)2+(2﹣1)2=10为偶数.请把10的一半表示为两个正整数的平方和;
(2)探究:设“发现”中的两个已知正整数为m,n,请论证“发现”中的结论正确.
(3)延伸:两个相邻奇数的平方差一定是8的倍数,这个命题是 命题(填“真或假”)
得分 评卷人 26.(本题12分)
某公司购买了一批物资.调查得知,2辆小货车与3辆大货车一次可以满载运输1800件;3辆小货车与4辆大货车一次可以满载运输2500件.
(1)求1辆大货车和1辆小货车一次可以分别满载运输多少件物资?
(2)现有3100件物资需要运往唐山,准备同时租用这两种货车,每辆均全部装满货
物,有几种租车方案?请写出所有租车方案.
七年级数学答案
一、1-5CDBDC 6-10ACCAB 11-16 CCDDBD
二、17. a4 18.假 19.合理即可 20. 12,
21. 解:
①×2得2 x+4 y=0③……………2分
②﹣③得:
x=6…………………4分
把x=6带入①中
解得:y=﹣3………………6分
所以原方程组的解为:.…………………8分
22. 解:(1+x)(1﹣x)+x(x+2)
=1﹣x2+x2+2x……………..4分(对一项得1分)
=1+2x…………6分
当x=时,原式=1+=1+1=2.……………8分
23. 解:(1)4,3.………………4分
(2)图略:……………6分
(3)>…………8分
垂线段最短…………….10分
24. 证明:(1)∵∠1=48°,∠2=132°,
∴∠1+∠2=180°…………2分
∴BD∥CE;………………5分
(2)∵BD∥CE,
∴∠C=∠ABD……………7分
又∵∠C=∠D,
∴∠ABD=∠D…………9分
∴AC∥DF…………10分
∴∠A=∠F……………11分
25. 解:验证:10的一半为5,
5=1+4=12+22………………3分
(m+n)2+(m﹣n)2
=m2+2mn+n2+m2﹣2mn+n2………………6分
=2m2+2n2………………7分
=2(m2+n2)……………8分
故两个已知正整数之和与这两个正整数之差的平方和一定是偶数,且该偶数的一半也可以表示为两个正整数的平方和…………9分
(3)真………………11分
26. 解:(1)设1辆小货车一次可满载运输x件物资,1辆大货车一次可满载运输y件物资
由题意可得:…………………5分
解得:……………………8分
答:1辆小货车一次可以满载运输300件物资,1辆大货车一次可以满载运输400件物资.
(2)解:设租用小货车a辆,大货车b辆,
依题意得:300a+400b=3100……………9分
∴.
又∵a,b均为正整数,
∴或或,
∴共有3种租车方案,方案1:租用9辆小货车,1辆大货车;
方案2:租用5辆小货车,4辆大货车;
方案3:租用1辆小货车,7辆大货车.…………………12分(写对一个方案得1分)
同课章节目录
