山东省济宁市微山县2022--2023学年七年级下学期期中考试数学试题(图片版含答案)
文档属性
| 名称 | 山东省济宁市微山县2022--2023学年七年级下学期期中考试数学试题(图片版含答案) |  | |
| 格式 | |||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 16:09:32 | ||
图片预览


文档简介
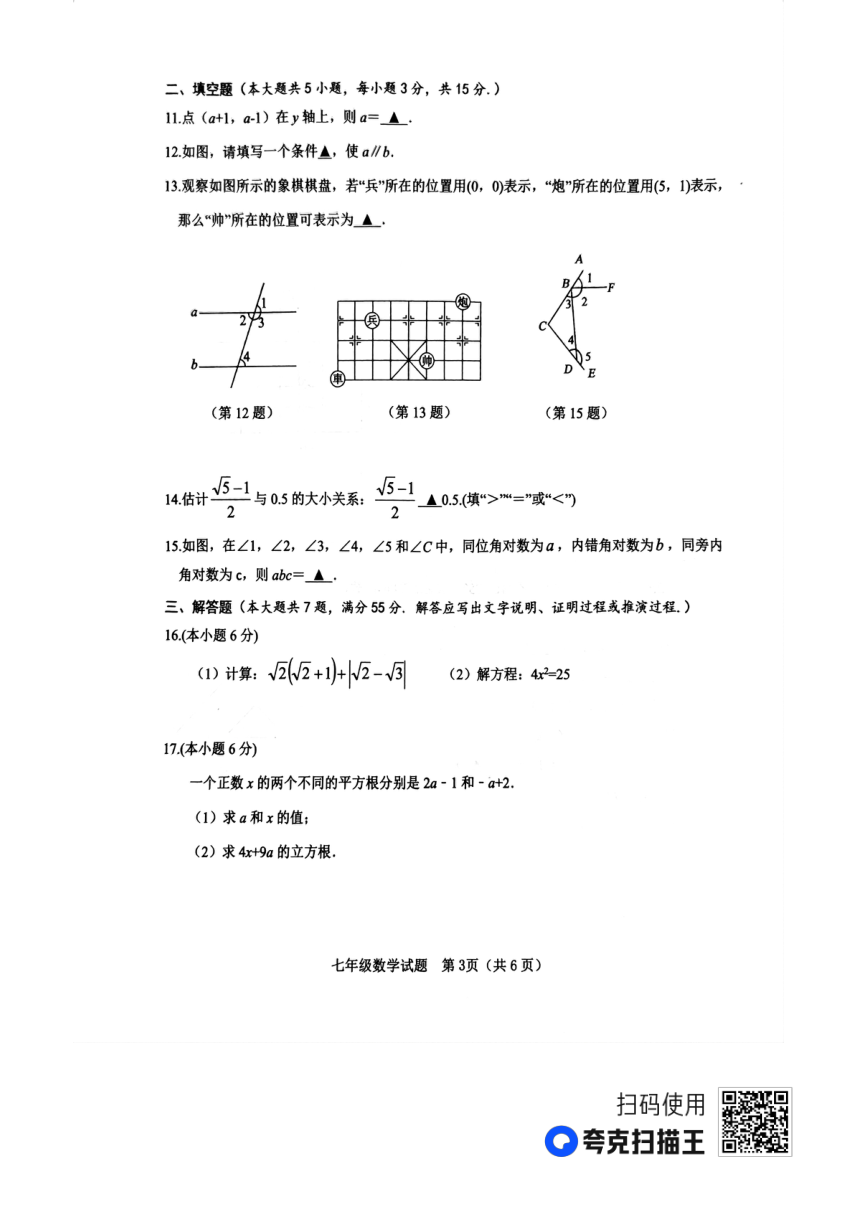
2022—2023 学年度第二学期期中考试 点 P移动的时间:(3+2+1)÷1=6秒;
故当点 P到 x轴的距离为 2个单位长度时,点 P移动的时间为 2秒或 6 秒.……8 分
21.(1)4; 23 -4;………………………………………………4 分
(2)解:∵1< 3<2,
一、选择题:每小题 3分,满分 30 分
题号 1 2 3 4 5 6 7 8 9 10 ∴9+1<9+ 3<9+2.
答案 D B A D C C B A B A
10<9+ 3<11.…………………………………………6分
二、填空题:本题共 5小题,每题 3分,共 15 分 ∵x是整数,且 0 < y < 1,
11.-1; 12.∠1=∠4(答案不唯一); 13.(3,-2); 14.>; 15.16.
∴x=10, y =9+ 3 -10= 3 -1.…………………………………8分
三、解答题:本题共 7小题,共 55分.要写出必要的文字说明或演算步骤.
16.(1)原式= 2 2 3 2 2 3 . ……………………………………3分 ∴x-y=11- 3.………………………………………………………9 分
x 5 22.(1)答:AB∥CD.(2) .………………………………………………………………………6分
2
理由:∵∠1=∠2,∠2=∠EFD,
17.解:(1)由题意可知:2a﹣1+(﹣a+2)=0,
∴∠1=∠EFD.
解得:a=﹣1.……………………………………………………………………1.5 分
∴AB∥CD.……………………………………………………3分
∴x=(2a﹣1)2=(﹣3)2=9;……………………………………………3 分
(2)证明:∵AB∥CD,
(2)4x+9a=4×9+9×(﹣1)=27,………………………………………4.5 分
∴∠BEF+∠EFD=180°,
∴ 3 27 =3.……………………………………………………6 分 又∵∠BEF与∠EFD的角平分线交于点 P,
1
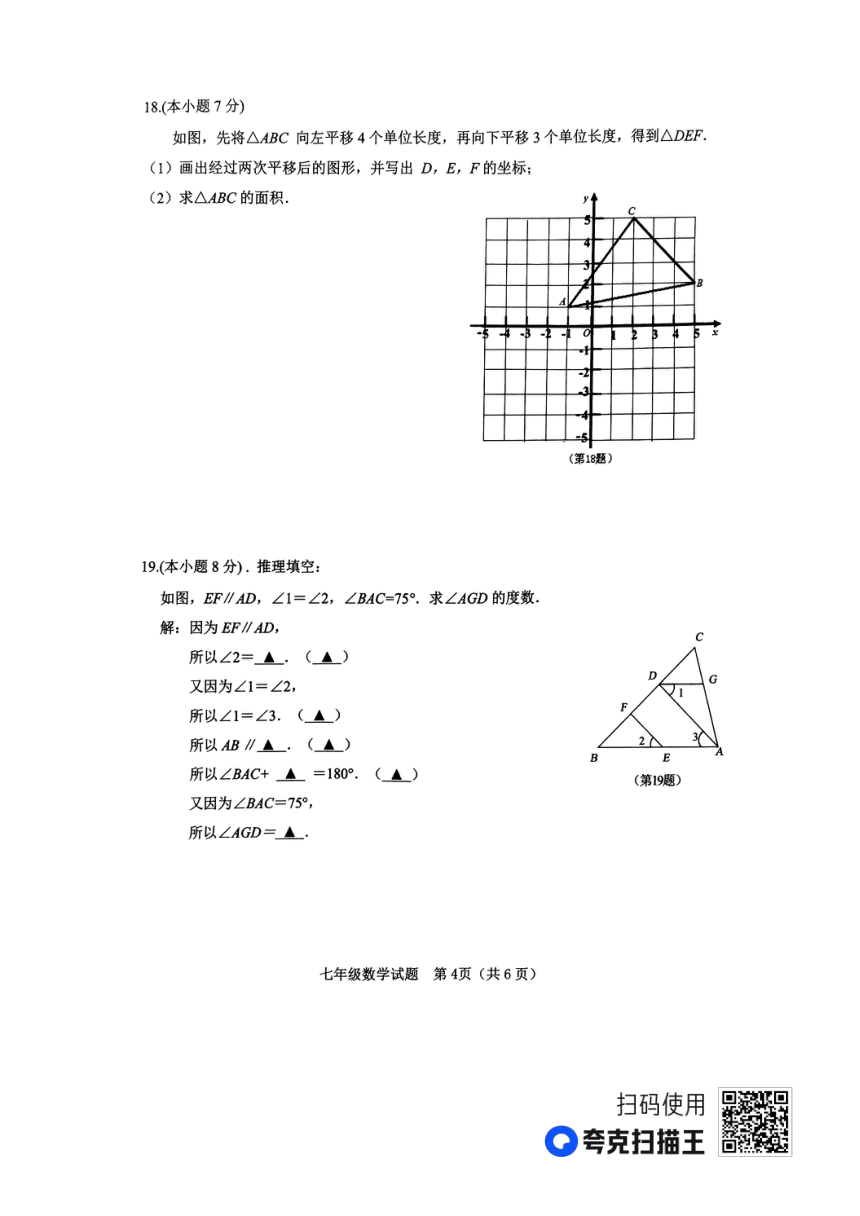
18.(1)画图:如图所示;……………………………………1 分 ∴∠PEF+∠EFP= (∠BEF+∠EFD)=90°,
2
D(-5,-2),E(1,-1),F(-2,2) ……………………………………4分
∴∠EPF=90°,即 EG⊥PF,
S 6 4 1 3 3 1 1 6 1(2)解: △ ABC 3 4 10.5.……7 分2 2 2 ∵GH⊥EG,
19.∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行; ∴PF∥GH.……………………………………………………6 分
∠AGD;两直线平行,同旁内角互补;105°.…………………………8 分(每空 1 分) (3)答:∠HPQ与∠HGE存在一定的数量关系,2∠HPQ=∠HGE.
20.(1)P(1,3);…………………………………………………………3 分 证明:∵∠PKG=2∠HPK,GH⊥EG,
(2)解:①当点 P在 OC上时,
∴∠KPG=90°-∠PKG=90°-2∠HPK,
点 P移动的时间:2÷1=2秒;……………………………………5分
∴∠EPK=180°-∠KPG=90°+2∠HPK,
②当点 P在 AB上时,
∵PQ平分∠EPK,
七年级数学参考答案第 1 页 共 3 页 七年级数学参考答案第 2 页 共 3 页
1
∴∠QPK= ∠EPK=45°+∠HPK,
2
∴∠HPQ=∠QPK-∠HPK=45°,
∴2∠HPQ=∠HGE.………………………………11 分
七年级数学参考答案第 3 页 共 3 页
故当点 P到 x轴的距离为 2个单位长度时,点 P移动的时间为 2秒或 6 秒.……8 分
21.(1)4; 23 -4;………………………………………………4 分
(2)解:∵1< 3<2,
一、选择题:每小题 3分,满分 30 分
题号 1 2 3 4 5 6 7 8 9 10 ∴9+1<9+ 3<9+2.
答案 D B A D C C B A B A
10<9+ 3<11.…………………………………………6分
二、填空题:本题共 5小题,每题 3分,共 15 分 ∵x是整数,且 0 < y < 1,
11.-1; 12.∠1=∠4(答案不唯一); 13.(3,-2); 14.>; 15.16.
∴x=10, y =9+ 3 -10= 3 -1.…………………………………8分
三、解答题:本题共 7小题,共 55分.要写出必要的文字说明或演算步骤.
16.(1)原式= 2 2 3 2 2 3 . ……………………………………3分 ∴x-y=11- 3.………………………………………………………9 分
x 5 22.(1)答:AB∥CD.(2) .………………………………………………………………………6分
2
理由:∵∠1=∠2,∠2=∠EFD,
17.解:(1)由题意可知:2a﹣1+(﹣a+2)=0,
∴∠1=∠EFD.
解得:a=﹣1.……………………………………………………………………1.5 分
∴AB∥CD.……………………………………………………3分
∴x=(2a﹣1)2=(﹣3)2=9;……………………………………………3 分
(2)证明:∵AB∥CD,
(2)4x+9a=4×9+9×(﹣1)=27,………………………………………4.5 分
∴∠BEF+∠EFD=180°,
∴ 3 27 =3.……………………………………………………6 分 又∵∠BEF与∠EFD的角平分线交于点 P,
1
18.(1)画图:如图所示;……………………………………1 分 ∴∠PEF+∠EFP= (∠BEF+∠EFD)=90°,
2
D(-5,-2),E(1,-1),F(-2,2) ……………………………………4分
∴∠EPF=90°,即 EG⊥PF,
S 6 4 1 3 3 1 1 6 1(2)解: △ ABC 3 4 10.5.……7 分2 2 2 ∵GH⊥EG,
19.∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行; ∴PF∥GH.……………………………………………………6 分
∠AGD;两直线平行,同旁内角互补;105°.…………………………8 分(每空 1 分) (3)答:∠HPQ与∠HGE存在一定的数量关系,2∠HPQ=∠HGE.
20.(1)P(1,3);…………………………………………………………3 分 证明:∵∠PKG=2∠HPK,GH⊥EG,
(2)解:①当点 P在 OC上时,
∴∠KPG=90°-∠PKG=90°-2∠HPK,
点 P移动的时间:2÷1=2秒;……………………………………5分
∴∠EPK=180°-∠KPG=90°+2∠HPK,
②当点 P在 AB上时,
∵PQ平分∠EPK,
七年级数学参考答案第 1 页 共 3 页 七年级数学参考答案第 2 页 共 3 页
1
∴∠QPK= ∠EPK=45°+∠HPK,
2
∴∠HPQ=∠QPK-∠HPK=45°,
∴2∠HPQ=∠HGE.………………………………11 分
七年级数学参考答案第 3 页 共 3 页
同课章节目录
