多项式乘以多项式[上学期]
图片预览





文档简介
课件13张PPT。14.2节 整式的乘法 3. 多项式与多项式相乘上官乡中心学校 陈燕萍多项式与多项式相乘情景模拟:
一、我(m) 与两位同学代表(a) 、(b)握手 二、我(m)与听课教师(n)与两位同学代表(a)、(b)握手
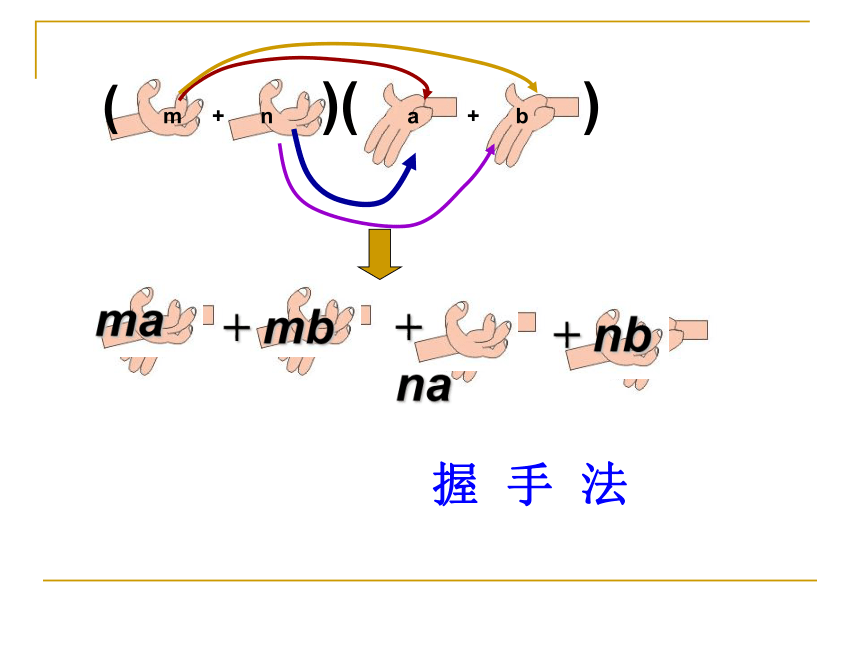
&( m + n )( a + b )
ma+ mb+ na+ nb握 手 法(m+n)(a+b)=ma+ mb+ na+ nb多项式乘以多项式法则: 先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。握 手 法例题解析一、尝试练习,信息反馈 1、尝试题: (1) (a-b)(c-d) (2) (2x + 5y)(3x?2y)(a - b)(c - d)
解: 原式= ac-ad-bc+bd
(2)(2x +5 y)(3x?2y)
解: 原式 =6x2?4xy + 15xy?10y2
= 6x2 +11xy?10y2 (3x + 4y)(3x - 4y)
(x + y)(2x2y - 4xy2)
(2x + 1)(4x2 - 2 x + 1)计算:聪明的一休考考你 :
1、计算:(1)(x +1) (x +2)(x -3)
(2)(2x +5) 2
2、化简求值:(x +2) (x -3)-(x +5 ) (x - 1), 其中x = -1/5
3、解方程: 2x (x -3)-(x -3 ) (x +8) = x2 +10
二、变式与提高挑战自我 1、(m+n)(a+b)的积有___项, 所以,多项式乘以多项式的积的项数,在没有合并同类项之前应等于多项式项数之积。496mn(m+n)(a+b+c)的积有____项,( m+n+p)(a+b+c)的积有___项,一般地(a1+ a2+ …+am)(b1+ b2…+bn)的积有________项,挑战自我2、(x – 1) (x – 2)的积中x项的系数为____,常数项为______, (4x – 3)(x2 + x – 1)的积中x2项的系数为____.
1-32(一)学医生 开处方 (1) (2x- 1) (x + 3)= 2x2 - 3
(2)(x + 2 ) 2 = x2 +4
(3) (x+1) (x -2)- (x+2) (x + 3)
= x2 -2x+x-2- x2 +3x+2x+6
= 4x +4 2x2 +5x - 3 x2 +4 x+4 ( )
-6x -8三、小结本节课你的收获是什么?(二)本节课你的收获是什么?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 如何进行多项式与多项式乘法运算?握手法
谢谢!再见回顾与思考② 再把所得的积相加。 ① 将单项式分别乘以多项式的每一项;① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.口答:(1)3a(2 a+1)
&
一、我(m) 与两位同学代表(a) 、(b)握手 二、我(m)与听课教师(n)与两位同学代表(a)、(b)握手
&( m + n )( a + b )
ma+ mb+ na+ nb握 手 法(m+n)(a+b)=ma+ mb+ na+ nb多项式乘以多项式法则: 先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。握 手 法例题解析一、尝试练习,信息反馈 1、尝试题: (1) (a-b)(c-d) (2) (2x + 5y)(3x?2y)(a - b)(c - d)
解: 原式= ac-ad-bc+bd
(2)(2x +5 y)(3x?2y)
解: 原式 =6x2?4xy + 15xy?10y2
= 6x2 +11xy?10y2 (3x + 4y)(3x - 4y)
(x + y)(2x2y - 4xy2)
(2x + 1)(4x2 - 2 x + 1)计算:聪明的一休考考你 :
1、计算:(1)(x +1) (x +2)(x -3)
(2)(2x +5) 2
2、化简求值:(x +2) (x -3)-(x +5 ) (x - 1), 其中x = -1/5
3、解方程: 2x (x -3)-(x -3 ) (x +8) = x2 +10
二、变式与提高挑战自我 1、(m+n)(a+b)的积有___项, 所以,多项式乘以多项式的积的项数,在没有合并同类项之前应等于多项式项数之积。496mn(m+n)(a+b+c)的积有____项,( m+n+p)(a+b+c)的积有___项,一般地(a1+ a2+ …+am)(b1+ b2…+bn)的积有________项,挑战自我2、(x – 1) (x – 2)的积中x项的系数为____,常数项为______, (4x – 3)(x2 + x – 1)的积中x2项的系数为____.
1-32(一)学医生 开处方 (1) (2x- 1) (x + 3)= 2x2 - 3
(2)(x + 2 ) 2 = x2 +4
(3) (x+1) (x -2)- (x+2) (x + 3)
= x2 -2x+x-2- x2 +3x+2x+6
= 4x +4 2x2 +5x - 3 x2 +4 x+4 ( )
-6x -8三、小结本节课你的收获是什么?(二)本节课你的收获是什么?运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.最后的计算结果要化简 ̄ ̄ ̄合并同类项. 如何进行多项式与多项式乘法运算?握手法
谢谢!再见回顾与思考② 再把所得的积相加。 ① 将单项式分别乘以多项式的每一项;① 不能漏乘:即单项式要乘遍多项式的每一项② 去括号时注意符号的确定.口答:(1)3a(2 a+1)
&
