第五章 圆复习学案
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章圆(复习)
【学习目标】
认识并掌握圆的有关概念和计算
理解并掌握与圆有关的位置关系
会进行弧长,扇形面积以及圆锥的有关计算
【课前梳理】
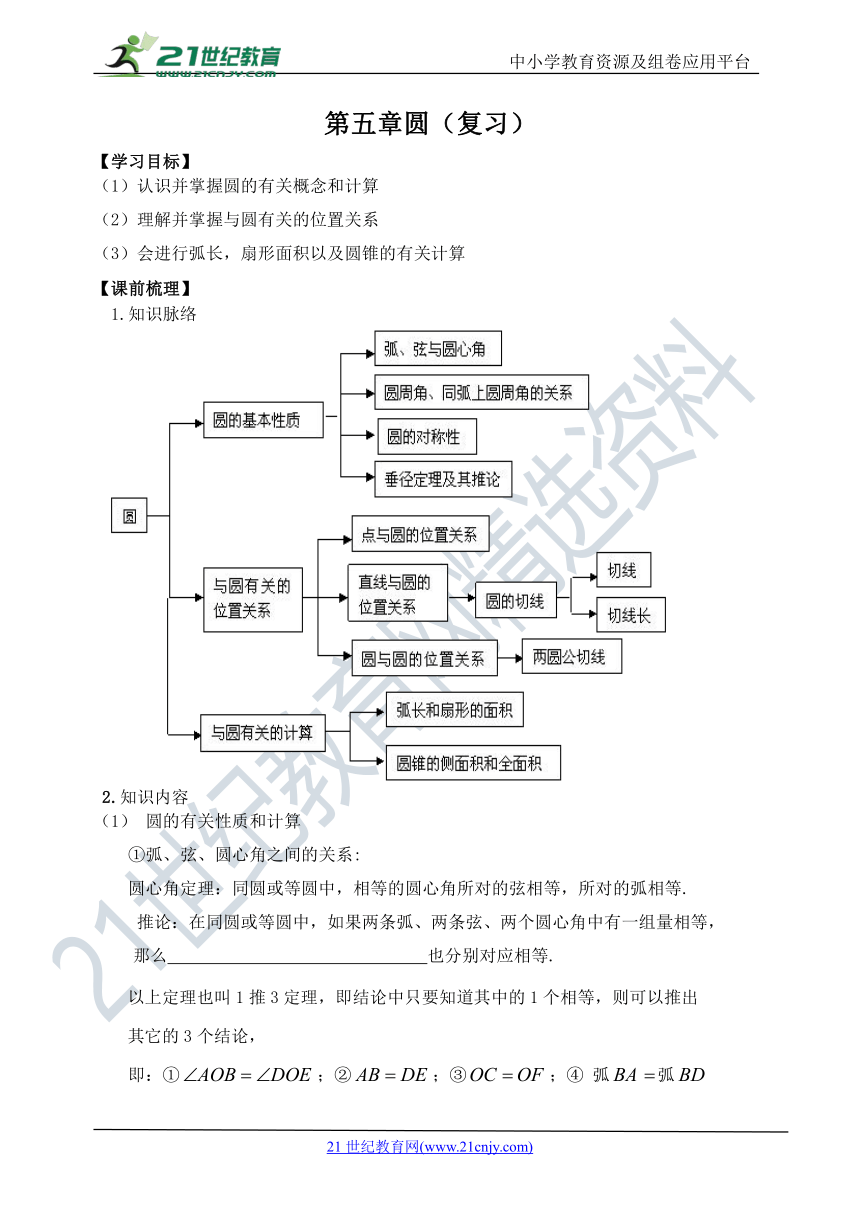
1.知识脉络
2.知识内容
(1) 圆的有关性质和计算
①弧、弦、圆心角之间的关系:
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等.
推论:在同圆或等圆中,如果两条弧、两条弦、两个圆心角中有一组量相等,
那么 也分别对应相等.
以上定理也叫1推3定理,即结论中只要知道其中的1个相等,则可以推出
其它的3个结论,
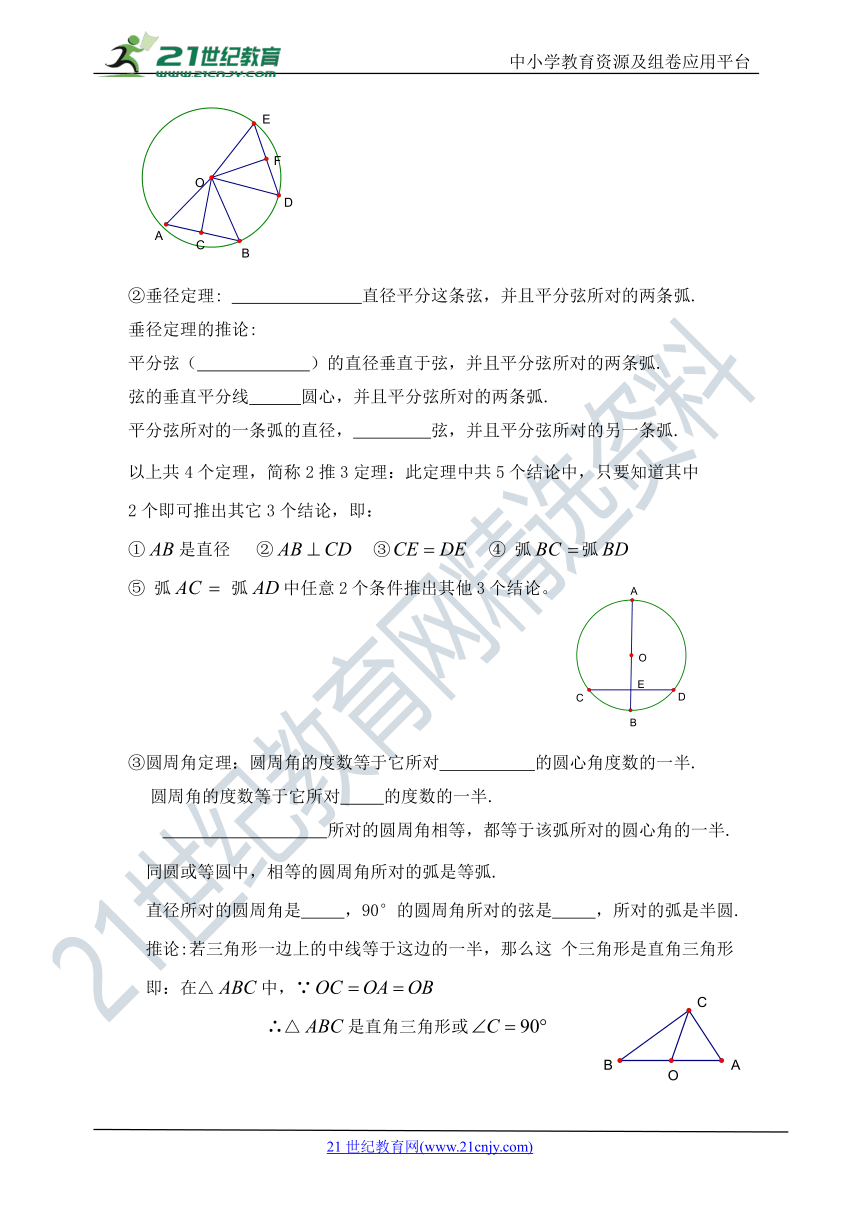
即:①;②;③;④ 弧弧
②垂径定理: 直径平分这条弦,并且平分弦所对的两条弧.
垂径定理的推论:
平分弦( )的直径垂直于弦,并且平分弦所对的两条弧.
弦的垂直平分线 圆心,并且平分弦所对的两条弧.
平分弦所对的一条弧的直径, 弦,并且平分弦所对的另一条弧.
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中
2个即可推出其它3个结论,即:
①是直径 ② ③ ④ 弧弧
⑤ 弧 弧中任意2个条件推出其他3个结论。
③圆周角定理:圆周角的度数等于它所对 的圆心角度数的一半.
圆周角的度数等于它所对 的度数的一半.
所对的圆周角相等,都等于该弧所对的圆心角的一半.
同圆或等圆中,相等的圆周角所对的弧是等弧.
直径所对的圆周角是 ,90°的圆周角所对的弦是 ,所对的弧是半圆.
推论:若三角形一边上的中线等于这边的一半,那么这 个三角形是直角三角形
即:在△中,∵
∴△是直角三角形或
④圆内接四边形的性质:
圆的内接四边形 ,并且任何一个外角等于它的 .
(2)点与圆的位置关系
①设点与圆心的距离为,圆的半径为,
则点在 ; 点在 ; 点在 .
②不在同一直线上的三点 一个圆. 一个三角形有且只有一个外接圆.
③三角形的外心是三角形 的交点.
三角形的外心到三角形的 的距离相等.
(3)直线与圆的位置关系
①设圆心到直线的距离为,圆的半径为,
则直线与圆相 ;直线与圆相 ;直线与圆相 .
②切线的性质:与圆只有 公共点;
圆心到切线的距离 半径;
圆的切线垂直于 的半径.
③切线的识别:如果一条直线与圆只有 公共点,那么这条直线是圆的切线.
到圆心的距离 半径的直线是圆的切线.
经过半径的外端且 这条半径的直线是圆的切线.
④三角形的内心是三角形三条 的交点.
三角形的内心到三角形 的距离相等.
⑤切线长:圆的切线上某一点与 之间的线段的长叫做这点到圆的切线长.
⑥切线长定理:从圆外一点引圆的 ,它们的切线长相等.
这一点和 的连线平分这两条切线的夹角.
(4)与圆有关的计算
①弧长公式: 扇形面积公式:
(其中为圆心角的度数,为半径)
②圆柱的侧面展开图是 形.
圆柱体也可以看成是一个 形以它的一边为轴旋转而形成的几何体.
圆柱的侧面积=底面 ×高
圆柱的全面积=侧面积+2×底面积
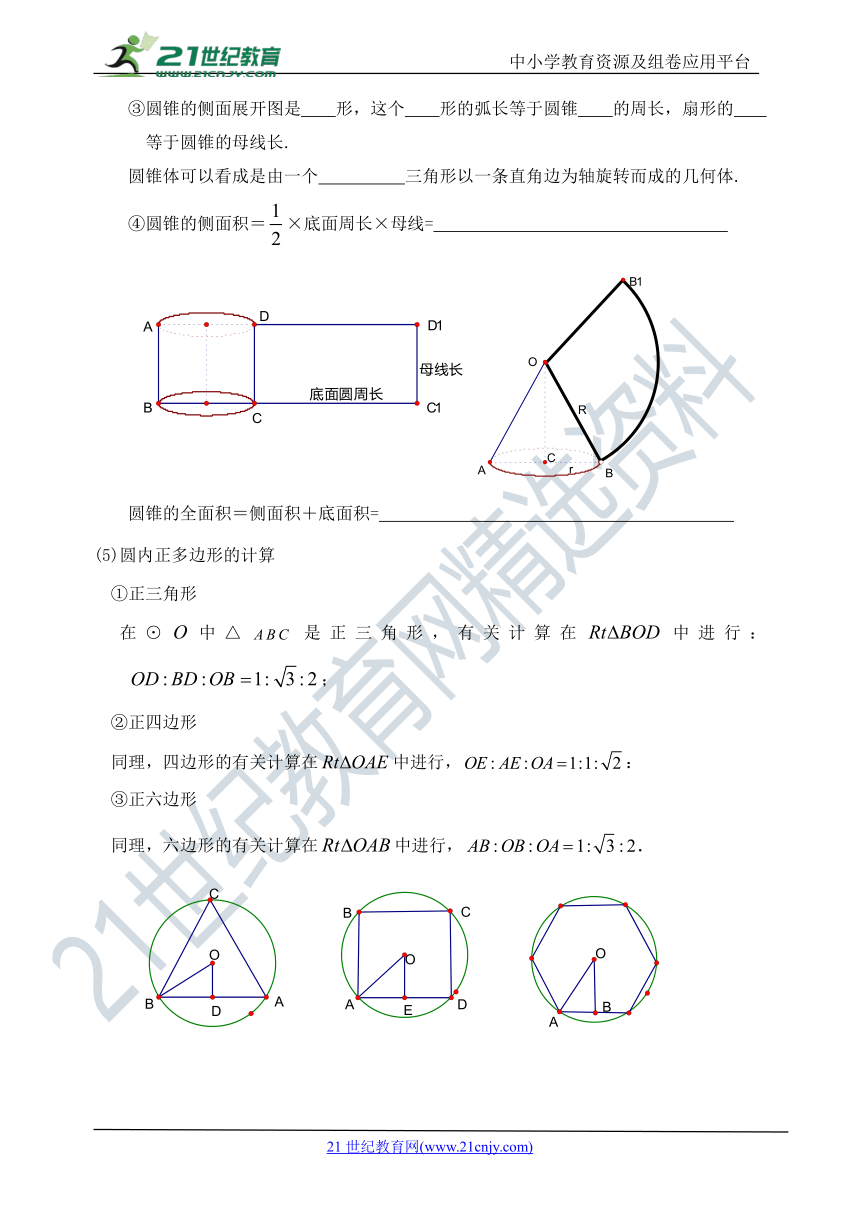
③圆锥的侧面展开图是 形,这个 形的弧长等于圆锥 的周长,扇形的 等于圆锥的母线长.
圆锥体可以看成是由一个 三角形以一条直角边为轴旋转而成的几何体.
④圆锥的侧面积=×底面周长×母线=
圆锥的全面积=侧面积+底面积=
(5)圆内正多边形的计算
①正三角形
在⊙中△是正三角形,有关计算在中进行:;
②正四边形
同理,四边形的有关计算在中进行,:
③正六边形
同理,六边形的有关计算在中进行,.
【课堂练习】
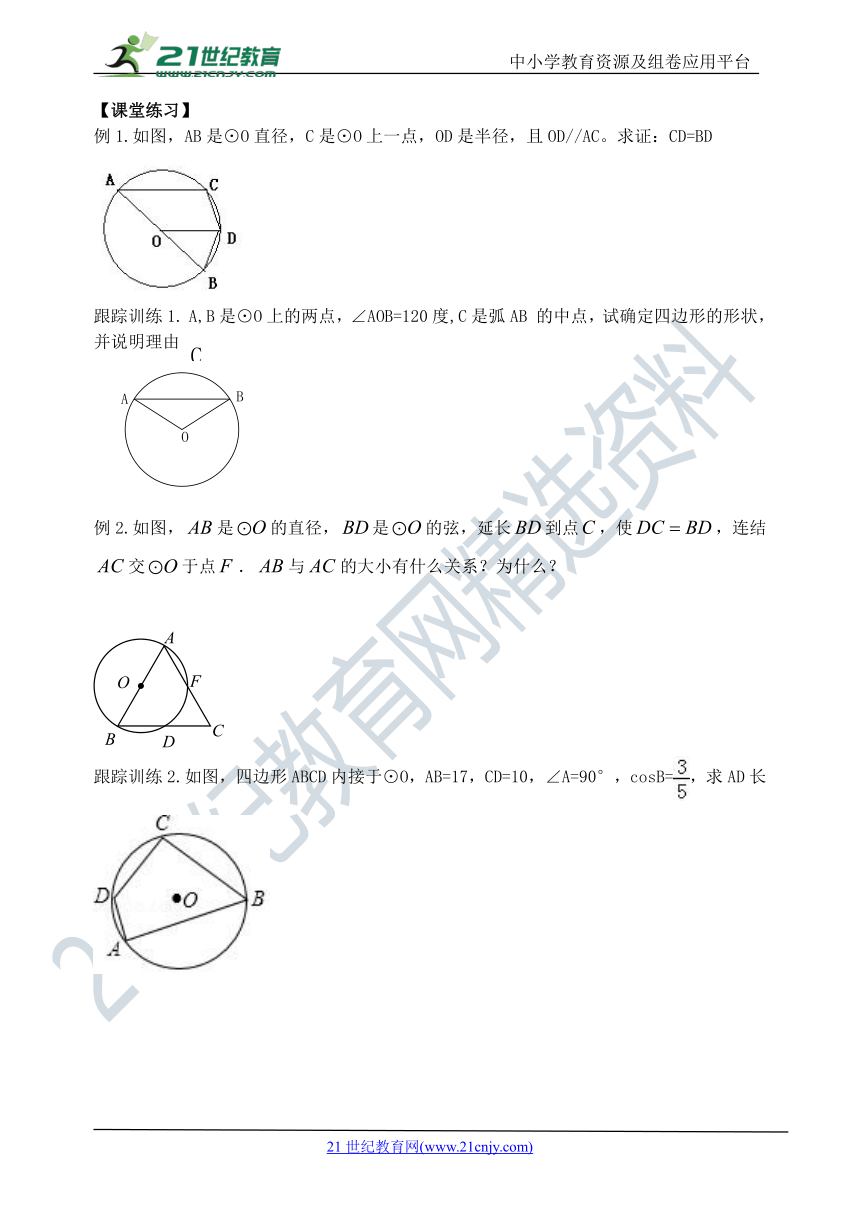
例1.如图,AB是⊙O直径,C是⊙O上一点,OD是半径,且OD//AC。求证:CD=BD
跟踪训练1. A,B是⊙O上的两点,∠AOB=120度,C是弧AB 的中点,试确定四边形的形状,并说明理由。
例2.如图,是的直径,是的弦,延长到点,使,连结交于点.与的大小有什么关系?为什么?
跟踪训练2.如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,cosB=,求AD长
例3.如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交
弦AC于点D,若AC=8cm,DE=2cm,求OD的长。
跟踪训练3.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?
.
例4.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.
跟踪训练4.如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ,CE的长是 .
例5.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
跟踪训练5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)
【巩固训练】
1.如图,内接于,若,则等于( )
B. C. D.
SHAPE \* MERGEFORMAT
如图,在半径为13的⊙O中,弦AB=10,点C是优弧上一点(不与A,B重合),则cosC的值为
3.工人师傅用一张半径为,圆心角为的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
4.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=60°,则∠E=
6.如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是 .
7.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
A.2 B.1 C. D.
8.正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,
求证:(1)四边形EBFD是矩形;
(2)DG=BE.
第五章复习学案答案
课堂练习
例1.
例2.
解:(1)
理由是:连接AD.
是的直径,
,即,
又,
;
(2)连接OD、OF.
中,,,
,
,
,
,
的度数是;
同理,
则
则的度数是,的度数是
跟踪训练2.,延长交的延长线于点
在中,,,
四边形内接于
答:的长为.
例3.解:
设OD=x,则OA=OE=x+2(cm).
∵E是弧AC的中点,
∴AC⊥OE,且AD=DC=AC=4cm,
在直角△AOD中,OA=OD+AD,
则(x+2)=16+x,
解得:x=3.
即OD=3cm.
跟踪训练3.
(1)证明:连接OD,
∵AB是直径,AB⊥CD,
∴弧BC=弧BD
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD,
∴∠CPD=∠COB.
(2)∠CP′D+∠COB=180 .
理由如下:连接OD,
∵∠CPD+∠CP′D=180 ,∠COB=∠DOB=12∠COD,
又∵∠CPD=∠COD,
∴∠COB=∠CPD,
∴∠CP′D+∠COB=180 .
例4.证明:(1)∵AB是☉O的直径,OD⊥AC,
∴弧CD=弧AD,
∴∠CBD=∠ABD,即BD平分∠ABC;
(2)连接AD,
∵OB=OD,
∴∠OBD=∠ODB=30 ,
由圆周角定理得,∠DOA=2∠ADB=60 ,
∴△AOD为等边三角形,
∴OD=OA,
∵∠DOA=60 ,∠C=90 ,
∴BC=12AB=OD.
跟踪训练4.
(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°-∠ACE﹦∠A,
∵C是的中点
∴
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2) ∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB=AC+BC,
又∵BC=CD,
∴AB=64+36=100,
∴AB=10,
∴
故⊙O的半径为5,CE的长是.
例5.
(1)如图,连接OE,
∵ED⊥EB,
∴∠DEB=90 ,
∴BD是⊙O的直径,
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
又∵∠C=90 ,
∴∠AEO=90 ,即OE⊥AC,
∴AC为⊙O的切线;
(2)∵ED⊥BE,
∴∠BED=∠C=90 ,
又∵∠DBE=∠EBC,
∴△BDE∽△BEC,
∴BD:BE=BE:BC,即=,
∴BC=;
∵∠AEO=∠C=90 ,∠A=∠A,
∴△AOE∽△ABC,
∴AO:AB=OE:BC,即,
解得:AD=.
跟踪训练5.
连接, 交于
平分,
是的切线.
是的中点,
,
,
,
是等边三角形,
,
巩固训练
D 2. 3. 4.D 5.90° 6. 7.C
8.
证明:(1)∵正方形ABCD内接于
∴∠BED=∠BAD=90 ,∠BFD=∠BCD=90 ,
又∵DF∥BE,
∴∠EDF+∠BED=180 ,
∴∠EDF=90 ,
∴四边形EBFD是矩形;
(2)∵正方形ABCD内接于
∴弧AD的度数是90 ,
∴∠AFD=45 ,
又∵∠GDF=90 ,
∴∠DGF=∠DFC=45 ,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
C
A
B
C
D
F
O
A
C
B
D
E
F
O
1题图
2题图
4题图
5题
6题
7题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第五章圆(复习)
【学习目标】
认识并掌握圆的有关概念和计算
理解并掌握与圆有关的位置关系
会进行弧长,扇形面积以及圆锥的有关计算
【课前梳理】
1.知识脉络
2.知识内容
(1) 圆的有关性质和计算
①弧、弦、圆心角之间的关系:
圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等.
推论:在同圆或等圆中,如果两条弧、两条弦、两个圆心角中有一组量相等,
那么 也分别对应相等.
以上定理也叫1推3定理,即结论中只要知道其中的1个相等,则可以推出
其它的3个结论,
即:①;②;③;④ 弧弧
②垂径定理: 直径平分这条弦,并且平分弦所对的两条弧.
垂径定理的推论:
平分弦( )的直径垂直于弦,并且平分弦所对的两条弧.
弦的垂直平分线 圆心,并且平分弦所对的两条弧.
平分弦所对的一条弧的直径, 弦,并且平分弦所对的另一条弧.
以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中
2个即可推出其它3个结论,即:
①是直径 ② ③ ④ 弧弧
⑤ 弧 弧中任意2个条件推出其他3个结论。
③圆周角定理:圆周角的度数等于它所对 的圆心角度数的一半.
圆周角的度数等于它所对 的度数的一半.
所对的圆周角相等,都等于该弧所对的圆心角的一半.
同圆或等圆中,相等的圆周角所对的弧是等弧.
直径所对的圆周角是 ,90°的圆周角所对的弦是 ,所对的弧是半圆.
推论:若三角形一边上的中线等于这边的一半,那么这 个三角形是直角三角形
即:在△中,∵
∴△是直角三角形或
④圆内接四边形的性质:
圆的内接四边形 ,并且任何一个外角等于它的 .
(2)点与圆的位置关系
①设点与圆心的距离为,圆的半径为,
则点在 ; 点在 ; 点在 .
②不在同一直线上的三点 一个圆. 一个三角形有且只有一个外接圆.
③三角形的外心是三角形 的交点.
三角形的外心到三角形的 的距离相等.
(3)直线与圆的位置关系
①设圆心到直线的距离为,圆的半径为,
则直线与圆相 ;直线与圆相 ;直线与圆相 .
②切线的性质:与圆只有 公共点;
圆心到切线的距离 半径;
圆的切线垂直于 的半径.
③切线的识别:如果一条直线与圆只有 公共点,那么这条直线是圆的切线.
到圆心的距离 半径的直线是圆的切线.
经过半径的外端且 这条半径的直线是圆的切线.
④三角形的内心是三角形三条 的交点.
三角形的内心到三角形 的距离相等.
⑤切线长:圆的切线上某一点与 之间的线段的长叫做这点到圆的切线长.
⑥切线长定理:从圆外一点引圆的 ,它们的切线长相等.
这一点和 的连线平分这两条切线的夹角.
(4)与圆有关的计算
①弧长公式: 扇形面积公式:
(其中为圆心角的度数,为半径)
②圆柱的侧面展开图是 形.
圆柱体也可以看成是一个 形以它的一边为轴旋转而形成的几何体.
圆柱的侧面积=底面 ×高
圆柱的全面积=侧面积+2×底面积
③圆锥的侧面展开图是 形,这个 形的弧长等于圆锥 的周长,扇形的 等于圆锥的母线长.
圆锥体可以看成是由一个 三角形以一条直角边为轴旋转而成的几何体.
④圆锥的侧面积=×底面周长×母线=
圆锥的全面积=侧面积+底面积=
(5)圆内正多边形的计算
①正三角形
在⊙中△是正三角形,有关计算在中进行:;
②正四边形
同理,四边形的有关计算在中进行,:
③正六边形
同理,六边形的有关计算在中进行,.
【课堂练习】
例1.如图,AB是⊙O直径,C是⊙O上一点,OD是半径,且OD//AC。求证:CD=BD
跟踪训练1. A,B是⊙O上的两点,∠AOB=120度,C是弧AB 的中点,试确定四边形的形状,并说明理由。
例2.如图,是的直径,是的弦,延长到点,使,连结交于点.与的大小有什么关系?为什么?
跟踪训练2.如图,四边形ABCD内接于⊙O,AB=17,CD=10,∠A=90°,cosB=,求AD长
例3.如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交
弦AC于点D,若AC=8cm,DE=2cm,求OD的长。
跟踪训练3.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.
(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠COB有什么数量关系?
.
例4.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.
跟踪训练4.如图,AB是⊙O的直径,C是的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;(2)若CD ﹦6, AC ﹦8,则⊙O的半径为 ,CE的长是 .
例5.如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
跟踪训练5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是的中点,求阴影部分的面积(结果保留π和根号)
【巩固训练】
1.如图,内接于,若,则等于( )
B. C. D.
SHAPE \* MERGEFORMAT
如图,在半径为13的⊙O中,弦AB=10,点C是优弧上一点(不与A,B重合),则cosC的值为
3.工人师傅用一张半径为,圆心角为的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
4.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=60°,则∠E=
6.如图,半径为1的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是 .
7.如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是( )
A.2 B.1 C. D.
8.正方形ABCD内接于⊙O,如图所示,在劣弧上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,
求证:(1)四边形EBFD是矩形;
(2)DG=BE.
第五章复习学案答案
课堂练习
例1.
例2.
解:(1)
理由是:连接AD.
是的直径,
,即,
又,
;
(2)连接OD、OF.
中,,,
,
,
,
,
的度数是;
同理,
则
则的度数是,的度数是
跟踪训练2.,延长交的延长线于点
在中,,,
四边形内接于
答:的长为.
例3.解:
设OD=x,则OA=OE=x+2(cm).
∵E是弧AC的中点,
∴AC⊥OE,且AD=DC=AC=4cm,
在直角△AOD中,OA=OD+AD,
则(x+2)=16+x,
解得:x=3.
即OD=3cm.
跟踪训练3.
(1)证明:连接OD,
∵AB是直径,AB⊥CD,
∴弧BC=弧BD
∴∠COB=∠DOB=∠COD.
又∵∠CPD=∠COD,
∴∠CPD=∠COB.
(2)∠CP′D+∠COB=180 .
理由如下:连接OD,
∵∠CPD+∠CP′D=180 ,∠COB=∠DOB=12∠COD,
又∵∠CPD=∠COD,
∴∠COB=∠CPD,
∴∠CP′D+∠COB=180 .
例4.证明:(1)∵AB是☉O的直径,OD⊥AC,
∴弧CD=弧AD,
∴∠CBD=∠ABD,即BD平分∠ABC;
(2)连接AD,
∵OB=OD,
∴∠OBD=∠ODB=30 ,
由圆周角定理得,∠DOA=2∠ADB=60 ,
∴△AOD为等边三角形,
∴OD=OA,
∵∠DOA=60 ,∠C=90 ,
∴BC=12AB=OD.
跟踪训练4.
(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°-∠ACE﹦∠A,
∵C是的中点
∴
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2) ∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB=AC+BC,
又∵BC=CD,
∴AB=64+36=100,
∴AB=10,
∴
故⊙O的半径为5,CE的长是.
例5.
(1)如图,连接OE,
∵ED⊥EB,
∴∠DEB=90 ,
∴BD是⊙O的直径,
∵OB=OE,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠CBE,
∴∠OEB=∠CBE,
∴OE∥BC,
又∵∠C=90 ,
∴∠AEO=90 ,即OE⊥AC,
∴AC为⊙O的切线;
(2)∵ED⊥BE,
∴∠BED=∠C=90 ,
又∵∠DBE=∠EBC,
∴△BDE∽△BEC,
∴BD:BE=BE:BC,即=,
∴BC=;
∵∠AEO=∠C=90 ,∠A=∠A,
∴△AOE∽△ABC,
∴AO:AB=OE:BC,即,
解得:AD=.
跟踪训练5.
连接, 交于
平分,
是的切线.
是的中点,
,
,
,
是等边三角形,
,
巩固训练
D 2. 3. 4.D 5.90° 6. 7.C
8.
证明:(1)∵正方形ABCD内接于
∴∠BED=∠BAD=90 ,∠BFD=∠BCD=90 ,
又∵DF∥BE,
∴∠EDF+∠BED=180 ,
∴∠EDF=90 ,
∴四边形EBFD是矩形;
(2)∵正方形ABCD内接于
∴弧AD的度数是90 ,
∴∠AFD=45 ,
又∵∠GDF=90 ,
∴∠DGF=∠DFC=45 ,
∴DG=DF,
又∵在矩形EBFD中,BE=DF,
∴BE=DG.
C
A
B
C
D
F
O
A
C
B
D
E
F
O
1题图
2题图
4题图
5题
6题
7题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
