5.4圆周角和圆心角的关系(2) 导学案
文档属性
| 名称 | 5.4圆周角和圆心角的关系(2) 导学案 | 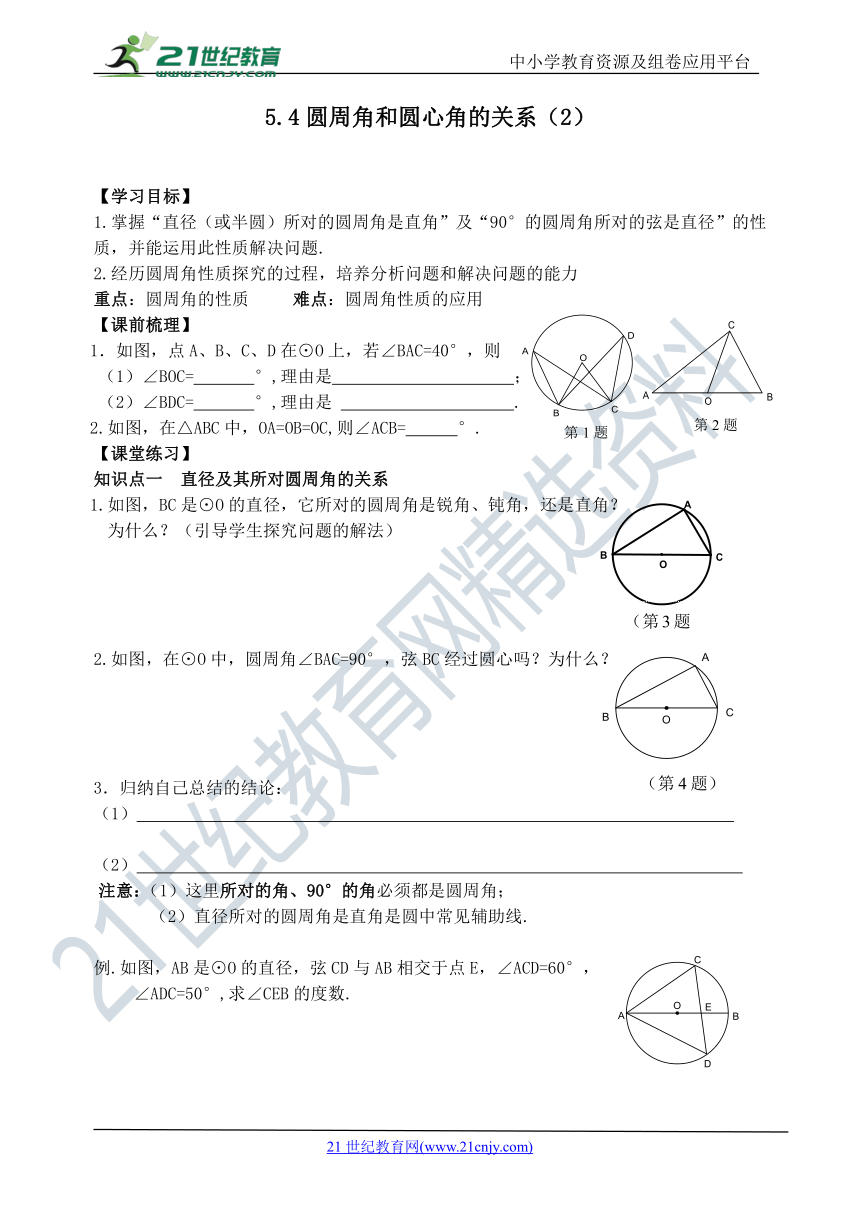 | |
| 格式 | doc | ||
| 文件大小 | 101.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 14:51:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.4圆周角和圆心角的关系(2)
【学习目标】
1.掌握“直径(或半圆)所对的圆周角是直角”及“90°的圆周角所对的弦是直径”的性质,并能运用此性质解决问题.
2.经历圆周角性质探究的过程,培养分析问题和解决问题的能力
重点:圆周角的性质 难点:圆周角性质的应用
【课前梳理】
1.如图,点A、B、C、D在⊙O上,若∠BAC=40°,则
(1)∠BOC= °,理由是 ;
(2)∠BDC= °,理由是 .
2.如图,在△ABC中,OA=OB=OC,则∠ACB= °.
【课堂练习】
知识点一 直径及其所对圆周角的关系
1.如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?
为什么?(引导学生探究问题的解法)
2.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?
3.归纳自己总结的结论:
(1)
(2)
注意:(1)这里所对的角、90°的角必须都是圆周角;
(2)直径所对的圆周角是直角是圆中常见辅助线.
例.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,
∠ADC=50°,求∠CEB的度数.
【当堂达标】
1.如图,AB是⊙O的直径,∠A=10°,则∠ABC=________.
2.如图,AB是⊙O的直径,CD是弦,∠ACD=40°,则∠BCD=_______,∠BOD=_______.
3.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,
使DC=BD,判断△ABC的 形 状:__________。
4.如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是( )
A. 30° B. 60° C. 90° D. 120°
5.如图,AB、CD是⊙O的直径,弦CE∥AB. 弧BD与弧BE相等吗?为什么?
【拓展延伸】
6.如图5,在中,在中,是直径,是弦,,垂足为,连接,则下列说法中正确的是( )
A. B. C. D.
7.如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点 D.
求BC和AD的长
5.4(2)
例.∠CEB=100°
当堂达标 1.80° 2.50°,100° 3.等腰三角形 4.D 5.略
D 7.BC=8,弧AD的长=
第2题
第1题
(第3题题)
(第4题)
第5题
(第7题)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.4圆周角和圆心角的关系(2)
【学习目标】
1.掌握“直径(或半圆)所对的圆周角是直角”及“90°的圆周角所对的弦是直径”的性质,并能运用此性质解决问题.
2.经历圆周角性质探究的过程,培养分析问题和解决问题的能力
重点:圆周角的性质 难点:圆周角性质的应用
【课前梳理】
1.如图,点A、B、C、D在⊙O上,若∠BAC=40°,则
(1)∠BOC= °,理由是 ;
(2)∠BDC= °,理由是 .
2.如图,在△ABC中,OA=OB=OC,则∠ACB= °.
【课堂练习】
知识点一 直径及其所对圆周角的关系
1.如图,BC是⊙O的直径,它所对的圆周角是锐角、钝角,还是直角?
为什么?(引导学生探究问题的解法)
2.如图,在⊙O中,圆周角∠BAC=90°,弦BC经过圆心吗?为什么?
3.归纳自己总结的结论:
(1)
(2)
注意:(1)这里所对的角、90°的角必须都是圆周角;
(2)直径所对的圆周角是直角是圆中常见辅助线.
例.如图,AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,
∠ADC=50°,求∠CEB的度数.
【当堂达标】
1.如图,AB是⊙O的直径,∠A=10°,则∠ABC=________.
2.如图,AB是⊙O的直径,CD是弦,∠ACD=40°,则∠BCD=_______,∠BOD=_______.
3.如图,AB是⊙O的直径,D是⊙O上的任意一点(不与点A、B重合),延长BD到点C,
使DC=BD,判断△ABC的 形 状:__________。
4.如图,AB是⊙O的直径,AC是弦,∠BAC=30°,则AC的度数是( )
A. 30° B. 60° C. 90° D. 120°
5.如图,AB、CD是⊙O的直径,弦CE∥AB. 弧BD与弧BE相等吗?为什么?
【拓展延伸】
6.如图5,在中,在中,是直径,是弦,,垂足为,连接,则下列说法中正确的是( )
A. B. C. D.
7.如图,在⊙O中,直径AB=10,弦AC=6,∠ACB的平分线交⊙O于点 D.
求BC和AD的长
5.4(2)
例.∠CEB=100°
当堂达标 1.80° 2.50°,100° 3.等腰三角形 4.D 5.略
D 7.BC=8,弧AD的长=
第2题
第1题
(第3题题)
(第4题)
第5题
(第7题)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
