5.6直线和圆的位置关系(3) 导学案
文档属性
| 名称 | 5.6直线和圆的位置关系(3) 导学案 |  | |
| 格式 | doc | ||
| 文件大小 | 111.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 14:51:41 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
5.6直线和圆的位置关系(3)
【学习目标】
1.掌握经过圆上一点画圆的切线的方法;
2.能够用切线的判定定理解决有关的论证和计算问题.
【课前梳理】
1.直线与圆相切的性质
⑴切线与圆有唯一的公共点; ⑵圆心到切线的距离等于半径;
⑶切线垂直于经过切点的半径.
2.切线的判定定理:经过半径的外端并且_____________________于这条半径的直线是圆的___________________.
3.直线是圆的切线的三个判定方法:
⑴与圆有唯一公共点的直线是圆的切线;
⑵到圆心的距离等于半径的直线是圆的切线;
⑶经过半径的外端并且垂直于这条半径的直线是圆的切线.
【课堂练习】
知识点一 切线的判定定理
1.已知直线AB经过⊙O上的一点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
2.已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为 半径作⊙O
求证:⊙O与AC相切。
【当堂达标】
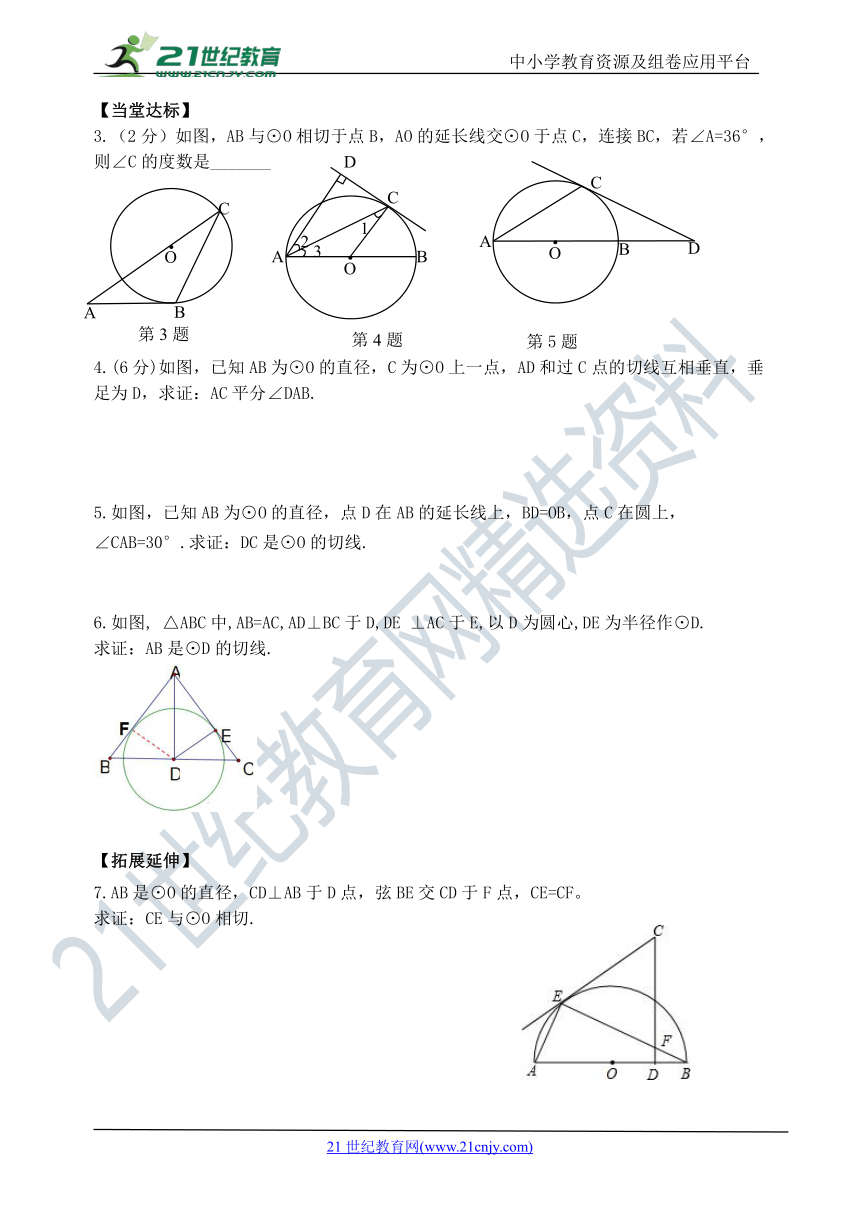
3.(2分)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°, 则∠C的度数是_______
第5题
4.(6分)如图,已知AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.
5.如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,
∠CAB=30°.求证:DC是⊙O的切线.
6.如图, △ABC中,AB=AC,AD⊥BC于D,DE ⊥AC于E,以D为圆心,DE为半径作⊙D.
求证:AB是⊙D的切线.
【拓展延伸】
7.AB是⊙O的直径,CD⊥AB于D点,弦BE交CD于F点,CE=CF。
求证:CE与⊙O相切.
5.6(3)
课堂练习
连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∵OC是⊙O的半径,
∴AB是圆O的切线.
2.
证明:如图所示,过O作OE⊥AC,垂足为E;
∵O为∠BAC平分线上一点,OD⊥AB于D,
∴OE=OD,
∵OE⊥AC,
∴⊙O与AC相切
3. 27°
4.
证明:连结OC,如图,
∵CD为⊙O的切线,
∴OC⊥AD,
∵AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠3,
∴∠2=∠3,
∴AC平分∠DAB.
5.
证明:连接OC、BC,
∵AB是⊙O的直径,
∴∠ACB=90
∵∠CAB=30
∴∠ABC=60
∵OB=OC,
∴△OBC为等边三角形
∴BC=OB=BD,△BCD为等腰三角形,∠CBD=120
∴∠BCD=30 ,
∴∠OCD=∠OCB+∠BCD=90
∴DC是⊙O的切线
6.
证明:
AB与⊙D相切,原因是
作DF⊥AB于F
∵AB=AC, AD⊥BC
∴ ∠BAD=∠CAD
∵DE⊥AC DF⊥AB
∴DE=DF
∵DE为⊙D半径
∴AB是⊙D的切线
7.
证明:连接OE
∵OB=OE
∴ ∠OBE=∠OEB
∵CE=CF
∴∠CEF=∠CFE=∠DFB
∵CD⊥AB于D
∴∠DFB+∠OBE=90
∴∠CEF+∠OEB=90 =∠CEO
∴CE⊥OE
∴CE与⊙O相切
·
A
B
C
D
O
·
1
3
2
A
B
C
D
O
第4题
·
C
B
O
A
第3题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.6直线和圆的位置关系(3)
【学习目标】
1.掌握经过圆上一点画圆的切线的方法;
2.能够用切线的判定定理解决有关的论证和计算问题.
【课前梳理】
1.直线与圆相切的性质
⑴切线与圆有唯一的公共点; ⑵圆心到切线的距离等于半径;
⑶切线垂直于经过切点的半径.
2.切线的判定定理:经过半径的外端并且_____________________于这条半径的直线是圆的___________________.
3.直线是圆的切线的三个判定方法:
⑴与圆有唯一公共点的直线是圆的切线;
⑵到圆心的距离等于半径的直线是圆的切线;
⑶经过半径的外端并且垂直于这条半径的直线是圆的切线.
【课堂练习】
知识点一 切线的判定定理
1.已知直线AB经过⊙O上的一点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.
2.已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为 半径作⊙O
求证:⊙O与AC相切。
【当堂达标】
3.(2分)如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°, 则∠C的度数是_______
第5题
4.(6分)如图,已知AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.
5.如图,已知AB为⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,
∠CAB=30°.求证:DC是⊙O的切线.
6.如图, △ABC中,AB=AC,AD⊥BC于D,DE ⊥AC于E,以D为圆心,DE为半径作⊙D.
求证:AB是⊙D的切线.
【拓展延伸】
7.AB是⊙O的直径,CD⊥AB于D点,弦BE交CD于F点,CE=CF。
求证:CE与⊙O相切.
5.6(3)
课堂练习
连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∵OC是⊙O的半径,
∴AB是圆O的切线.
2.
证明:如图所示,过O作OE⊥AC,垂足为E;
∵O为∠BAC平分线上一点,OD⊥AB于D,
∴OE=OD,
∵OE⊥AC,
∴⊙O与AC相切
3. 27°
4.
证明:连结OC,如图,
∵CD为⊙O的切线,
∴OC⊥AD,
∵AD⊥CD,
∴OC∥AD,
∴∠1=∠2,
∵OC=OA,
∴∠1=∠3,
∴∠2=∠3,
∴AC平分∠DAB.
5.
证明:连接OC、BC,
∵AB是⊙O的直径,
∴∠ACB=90
∵∠CAB=30
∴∠ABC=60
∵OB=OC,
∴△OBC为等边三角形
∴BC=OB=BD,△BCD为等腰三角形,∠CBD=120
∴∠BCD=30 ,
∴∠OCD=∠OCB+∠BCD=90
∴DC是⊙O的切线
6.
证明:
AB与⊙D相切,原因是
作DF⊥AB于F
∵AB=AC, AD⊥BC
∴ ∠BAD=∠CAD
∵DE⊥AC DF⊥AB
∴DE=DF
∵DE为⊙D半径
∴AB是⊙D的切线
7.
证明:连接OE
∵OB=OE
∴ ∠OBE=∠OEB
∵CE=CF
∴∠CEF=∠CFE=∠DFB
∵CD⊥AB于D
∴∠DFB+∠OBE=90
∴∠CEF+∠OEB=90 =∠CEO
∴CE⊥OE
∴CE与⊙O相切
·
A
B
C
D
O
·
1
3
2
A
B
C
D
O
第4题
·
C
B
O
A
第3题
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
