2.5 三角函数的应用(1) 导学案
图片预览
文档简介
中小学教育资源及组卷应用平台
2.5 三角函数的应用(1)
【学习目标】
1.理解仰角、俯角的意义,并将有关仰角、俯角的实际问题转化为解直角三角形.
【课前梳理】
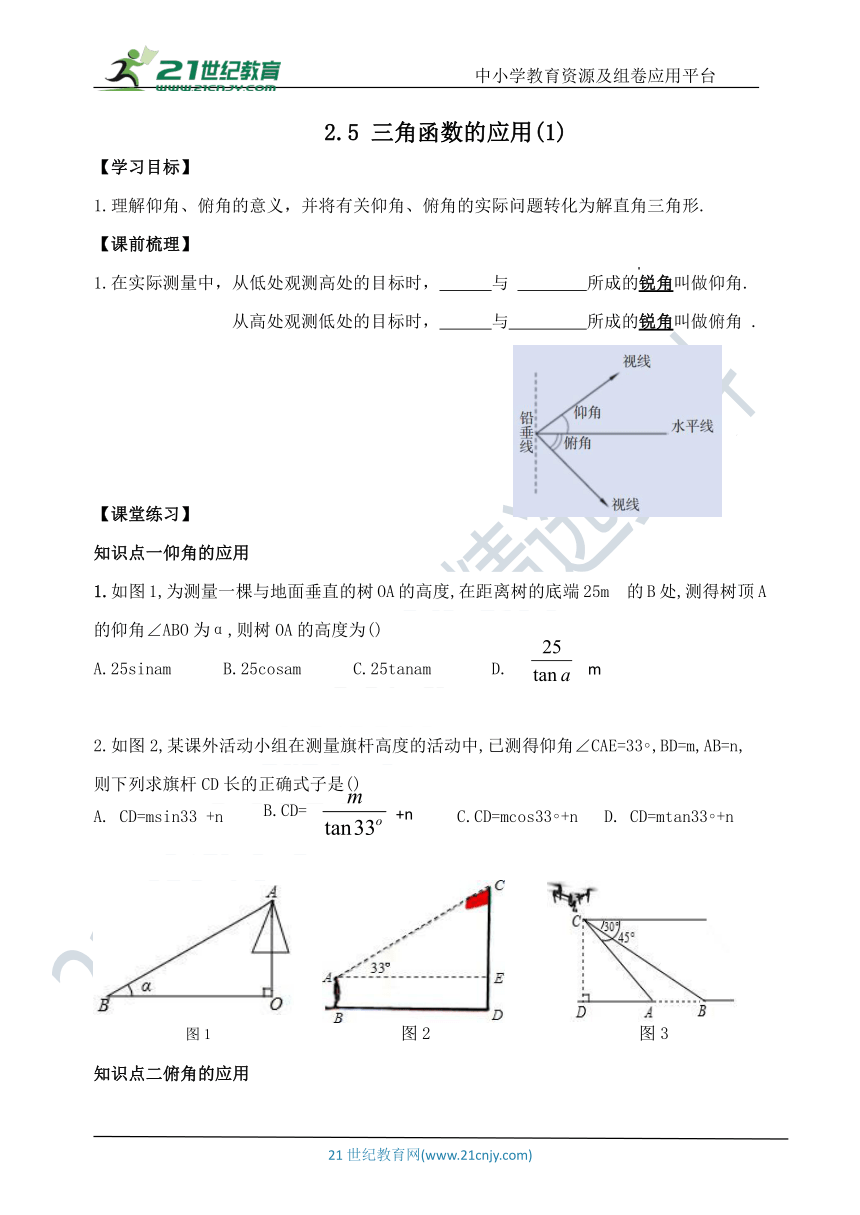
1.在实际测量中,从低处观测高处的目标时, 与 所成的锐角叫做仰角.
从高处观测低处的目标时, 与 所成的锐角叫做俯角 .
【课堂练习】
知识点一仰角的应用
1.如图1,为测量一棵与地面垂直的树OA的高度,在距离树的底端25m 的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为()
A.25sinam B.25cosam C.25tanam D.
2.如图2,某课外活动小组在测量旗杆高度的活动中,已测得仰角∠CAE=33 ,BD=m,AB=n, 则下列求旗杆CD长的正确式子是()
A. CD=msin33 +n C.CD=mcos33 +n D. CD=mtan33 +n
知识点二俯角的应用
3.如图3,某高速公路设计中需要测量某条江的宽度AB,测量人员使用无人机测量,在C处测得A,B两点的俯角分别为45 和30 .若无人机离地面的高度CD为1800m,且点A,B,D在同一水平直线上,求这条江的宽度AB长为 m(结果保留根号).
4.如图4,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为330米,点A. D.B在同一直线上,则AB两点的距离是___米.
【当堂检测】
1.如图5,一棵大树在一次强台风中于离地面6米处折断倒下,倒下部分与地面成45°夹角,这棵大树在折断前的高度为 米(结果保留根号).
2.如图6,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进30米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为 米
3.如图7,某人为了测量小山顶上的塔DE的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进48m到达山脚点B,测得塔尖点D的仰角为60 ,塔底点E的仰角为37°,求塔ED的高度.(结果保留根号)(sin37°≈ , cos37°≈ , tan37°≈ )
2.5三角函数的应用(1)
【课堂练习】1.C , 2.D, 3. (1800-1800), 4.(330+330)
【当堂达标】1. (6+6), 2. 15 3.塔ED的高度为 (54+6)m
m
+n
B.CD=
图1 图2 图3
45°
图4 图5 图6
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2.5 三角函数的应用(1)
【学习目标】
1.理解仰角、俯角的意义,并将有关仰角、俯角的实际问题转化为解直角三角形.
【课前梳理】
1.在实际测量中,从低处观测高处的目标时, 与 所成的锐角叫做仰角.
从高处观测低处的目标时, 与 所成的锐角叫做俯角 .
【课堂练习】
知识点一仰角的应用
1.如图1,为测量一棵与地面垂直的树OA的高度,在距离树的底端25m 的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为()
A.25sinam B.25cosam C.25tanam D.
2.如图2,某课外活动小组在测量旗杆高度的活动中,已测得仰角∠CAE=33 ,BD=m,AB=n, 则下列求旗杆CD长的正确式子是()
A. CD=msin33 +n C.CD=mcos33 +n D. CD=mtan33 +n
知识点二俯角的应用
3.如图3,某高速公路设计中需要测量某条江的宽度AB,测量人员使用无人机测量,在C处测得A,B两点的俯角分别为45 和30 .若无人机离地面的高度CD为1800m,且点A,B,D在同一水平直线上,求这条江的宽度AB长为 m(结果保留根号).
4.如图4,在直升机的镜头下,观测A处的俯角为30°,B处的俯角为45°,如果此时直升机镜头C处的高度CD为330米,点A. D.B在同一直线上,则AB两点的距离是___米.
【当堂检测】
1.如图5,一棵大树在一次强台风中于离地面6米处折断倒下,倒下部分与地面成45°夹角,这棵大树在折断前的高度为 米(结果保留根号).
2.如图6,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进30米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为 米
3.如图7,某人为了测量小山顶上的塔DE的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进48m到达山脚点B,测得塔尖点D的仰角为60 ,塔底点E的仰角为37°,求塔ED的高度.(结果保留根号)(sin37°≈ , cos37°≈ , tan37°≈ )
2.5三角函数的应用(1)
【课堂练习】1.C , 2.D, 3. (1800-1800), 4.(330+330)
【当堂达标】1. (6+6), 2. 15 3.塔ED的高度为 (54+6)m
m
+n
B.CD=
图1 图2 图3
45°
图4 图5 图6
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
