第二章 直角三角形的边角关系复习学案
图片预览



文档简介
中小学教育资源及组卷应用平台
直角三角形的边角关系复习
【学习目标】
1.准确理解锐角三角函数相关概念,熟练掌握30°,45°,60°等特殊角的三角函数值.
2.会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角.
3.熟练应用锐角三角函数解直角三角形及相关的实际问题.
【课前梳理】
一、锐角三角函数的相关概念
1.锐角的A的正弦、余弦、正切统称为 ;sinA= ;cosA= ;
tanA= ;其中 0<sinA<1, 0<cosA<1.
2.特殊角的三角函数值
sin30°= ; cos30°= ; tan30°= ;
sin45°= ; cos45°= ; tan45°= ;
sin60°= ; cos60°= ; tan60°= ;
二、解直角三角形及其应用
1.常见的几个数量关系
如图1所示,在Rt△ABC 中,∠C=90°,则∠A+∠B= ; a+b= ;
sinA= cosB= ; cosA= sinB= ; tanA= = ; .
2.解直角三角形的类型及解法 如图1所示:
已知条件 解法
一条边和一个锐角 斜边 c和锐角∠A ∠B= ,a= ,b=
直角边 a和锐∠A ∠B= ,b= ,c=
两条边 两条直角边 a和 b c= ,由 求∠A,∠B=
直角边 a和斜边 c b= ,由 求∠A,∠B=
3.解斜三角形的基本思路: ;注意不要拆解特殊角.
4.有关概念
(1)仰角与俯角:如图2,在进行测量时,从下向上看,视线与水平线的夹角叫做 ;从上往下看,视线与水平线的夹角叫做 .
(2)坡度与坡角:如图3,坡面的铅垂高度(h)与水平宽度(l)的比叫做坡面的
(或坡比),记作 i,即i= .坡度通常写成 h∶l的形式,如 i=1∶6;坡面与水平面的夹角叫做坡角,记作α,有i= = tanα,显然,坡度越大,坡角 a就 .坡面就 .
(3)方位角:指南或指北的方向线所成的小于90°角的为方位角.
【课堂练习】
知识点一特殊角的三角函数值与实数运算
典例1 tan30°sin60°+cos230°-sin230°tan45°
跟踪训练2
①tan60°+-3cos30°+-
②(﹣)﹣3﹣2cos45°+(3.14﹣π)0+= .
知识点二已知两边解直角三角形
典例3.如图3所示,在Rt△ABC 中,∠C=90°,a,b,c分别为∠A,∠B,∠C的边,a=3,b=3
解这个直角三角形.
跟踪训练4.如图4所示,∠ACB=90°,AB=17,AC=15, ∠BCM=∠BAC,求sin∠BAC的值和点B到直线MC的距离.
知识点三已知一角一边解直角三形
典例5如图5所示,在△ABC中,∠B=90°,∠C=60°,BC=9.求AC、AB的长.
跟踪训练6.如图6所示,已知,Rt△ABC中,∠C=90°,∠A=30°,BC=3,D为AC点,∠BDC=45°,求AB的长
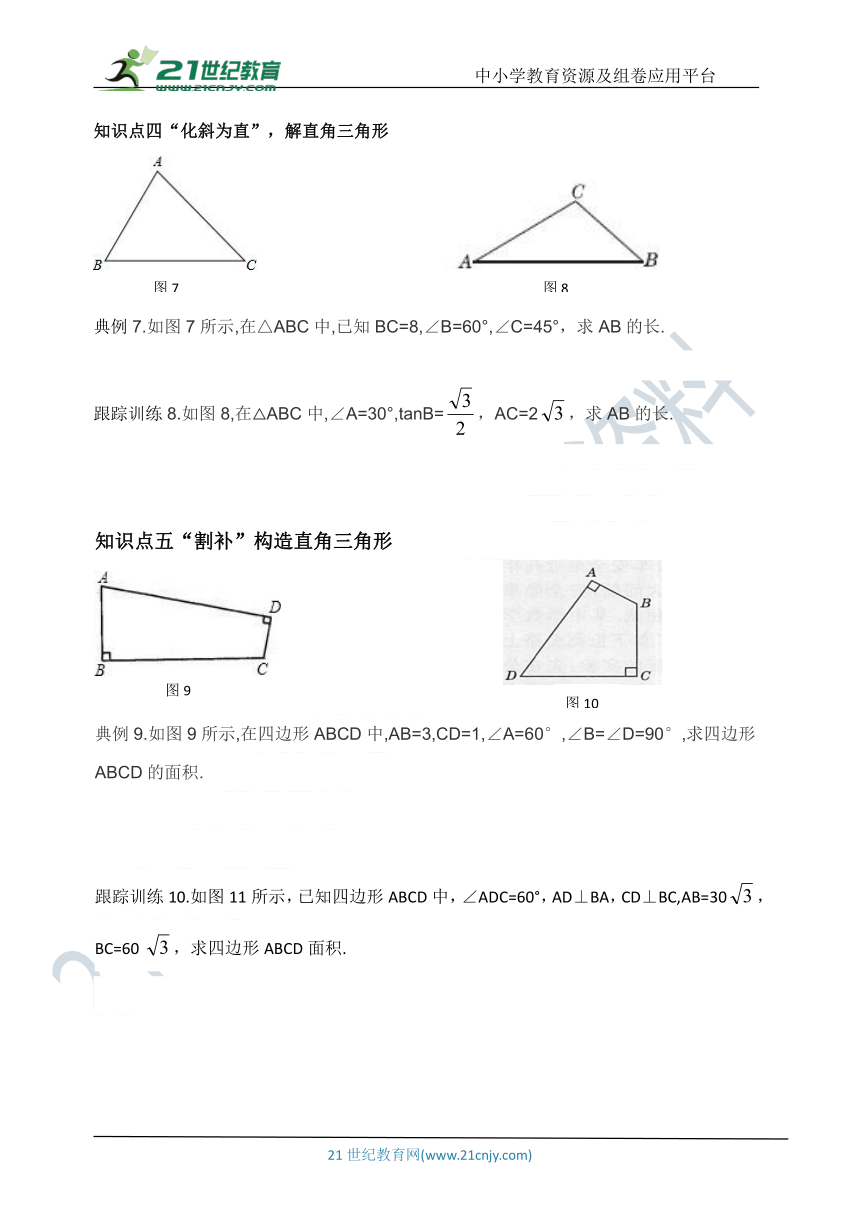
知识点四“化斜为直”,解直角三角形
典例7.如图7所示,在△ABC中,已知BC=8,∠B=60°,∠C=45°,求AB的长.
跟踪训练8.如图8,在△ABC中,∠A=30°,tanB=,AC=2,求AB的长.
知识点五“割补”构造直角三角形
典例9.如图9所示,在四边形ABCD中,AB=3,CD=1,∠A=60°,∠B=∠D=90°,求四边形ABCD的面积.
跟踪训练10.如图11所示,已知四边形ABCD中,∠ADC=60°,AD⊥BA,CD⊥BC,AB=30,BC=60 ,求四边形ABCD面积.
知识点六仰角、俯角问题
典例11.如图11所示,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45° 和30°若飞机离地面的高度CH为1500米,且点H,A,B在同一水平直线上,则这条江的宽度AB为______米 .(结果保留根号)
跟踪训练12.如图,从楼AB的A处测得对面楼CD的顶部C的仰角为 37°,底部D的俯角为 45°,两楼的水平距离BD为32m,那么楼CD的高度约为______m.
(结果精确到1m,参考数据: sin37 ≈0.6; cos37 ≈0.8; ; tan37 ≈0.75)
知识点七方向角、坡角问题
典例13.如图13所示,湖心岛上有一凉亭 B,在凉亭 B的正东湖边有一棵大树 A,在湖边的 C处测得 B在北偏西45°方向上,测得 A在北偏东30°方向上,又测得 B、 C之间的距离为120米,则A、 B之间的距离是 米.(结果保留根号形式)
跟踪训练14.如图14所示,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为______海里.
跟踪训练如图15所示,水坝的横断面是梯形ABCD,其中BC平行于AD,背水坡AB的坡角∠BAD=45°,坝高BE=20米,汛期来临,为加大水坝的防洪强度,将坝底从A处向后水平延伸到F处,使新的背水坡BF的坡角∠F=30°,则AF为 米.(结果精确到1米,参考数据:≈1.414,≈1.732)
知识点八三角函数与一次函数的结合
典例16..如图16所示,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB=.
求点B的坐标和一次函数表达式.
跟踪训练17.如图17所示,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.
【巩固训练】
1.小丽同学在校外实践活动中对某一黄河大桥开展测量活动.如图19所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.+ D.atanα+atanβ
2.在平面直角坐标系中,将一块直角三角板如图20所示放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数y=﹣(x<0),y=(x>0)的图象上,则sin∠ABO的值= .
3.如图21所示的网格是正方形网格,则∠PAB+∠PBA= .(点A,B,P是网格线交点)
4.如图22所示,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP= .
5.如图23所示,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=在第一象限内的图象经过点D,交BC于点E.若AB=6,CE=2BE,tan∠AOD=,则k的值为 .
6.如图24所示,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为 m.
(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
7.如图25所示,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为______.
8.如图26所示,在Rt△ABC中,∠C=90°,点D在BC边上,∠ADC=45°,BD=2,tanB=
求AC和AB的长; (2)求sin∠BAD的值.
9.如图27所示,某小岛B在港口A的南偏西63°方向上,某船从港口A出发沿北偏西72°的方向以每小时25海里的速度行驶了2小时到达C处,在C处测得小岛B在南偏西33°的方向上,求港口A与小岛B的距离
如图28所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为
(﹣2,0),且tan∠ACO=2.
求该反比例函数和一次函数的解析式;
(1)求点B的坐标;
(2)在x轴上求点E,使△ACE为直角三角形.(直接写出点E坐标)
直角三角形边角关系复习
【课堂练习】1.1, 2.3, 3.-7+,4.AB=6;∠A=30°;∠B=60°,5.sin∠BAC=;
MC=, 6.AC=18;AB=9 7.AD=3-3, 8.AB=8-1, 9.AB=5,
四边形ABCD面积=4 ,11. 四边形ABCD面积=4950 ,
12.(1500-1500), 14. (60+20),15.20, 15.56 16. 15,
17.B(,0);y=2x-1, 18.(1)y=x+1;y=,(2)x>2或-3【巩固训练】1.D, 2.,3.∠PAB+∠PBA=45°,4.tan∠HAP=,5. k= 6.BC为262m, 7.40(3+)米, 8,(1)AB==10,(2)sin∠BAD==, 9.AB=(25+25)海里, 10.(1)反比例函数表达式:y=;一次函数表达式:y=2x+4;(2)点B的坐标为(-3,-2);点E的坐标为(1,0)或(13,0).
图1
h
l
i=h:l
α
图2 图3
图3 图4 图5 图6
图7 图8
图10
图9
图11
图12
图12 图13
图13 图14 图15
图16 图17
图19 图20 图21
图22 图23 图24
图25 图26 图27
图28
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
直角三角形的边角关系复习
【学习目标】
1.准确理解锐角三角函数相关概念,熟练掌握30°,45°,60°等特殊角的三角函数值.
2.会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它的对应锐角.
3.熟练应用锐角三角函数解直角三角形及相关的实际问题.
【课前梳理】
一、锐角三角函数的相关概念
1.锐角的A的正弦、余弦、正切统称为 ;sinA= ;cosA= ;
tanA= ;其中 0<sinA<1, 0<cosA<1.
2.特殊角的三角函数值
sin30°= ; cos30°= ; tan30°= ;
sin45°= ; cos45°= ; tan45°= ;
sin60°= ; cos60°= ; tan60°= ;
二、解直角三角形及其应用
1.常见的几个数量关系
如图1所示,在Rt△ABC 中,∠C=90°,则∠A+∠B= ; a+b= ;
sinA= cosB= ; cosA= sinB= ; tanA= = ; .
2.解直角三角形的类型及解法 如图1所示:
已知条件 解法
一条边和一个锐角 斜边 c和锐角∠A ∠B= ,a= ,b=
直角边 a和锐∠A ∠B= ,b= ,c=
两条边 两条直角边 a和 b c= ,由 求∠A,∠B=
直角边 a和斜边 c b= ,由 求∠A,∠B=
3.解斜三角形的基本思路: ;注意不要拆解特殊角.
4.有关概念
(1)仰角与俯角:如图2,在进行测量时,从下向上看,视线与水平线的夹角叫做 ;从上往下看,视线与水平线的夹角叫做 .
(2)坡度与坡角:如图3,坡面的铅垂高度(h)与水平宽度(l)的比叫做坡面的
(或坡比),记作 i,即i= .坡度通常写成 h∶l的形式,如 i=1∶6;坡面与水平面的夹角叫做坡角,记作α,有i= = tanα,显然,坡度越大,坡角 a就 .坡面就 .
(3)方位角:指南或指北的方向线所成的小于90°角的为方位角.
【课堂练习】
知识点一特殊角的三角函数值与实数运算
典例1 tan30°sin60°+cos230°-sin230°tan45°
跟踪训练2
①tan60°+-3cos30°+-
②(﹣)﹣3﹣2cos45°+(3.14﹣π)0+= .
知识点二已知两边解直角三角形
典例3.如图3所示,在Rt△ABC 中,∠C=90°,a,b,c分别为∠A,∠B,∠C的边,a=3,b=3
解这个直角三角形.
跟踪训练4.如图4所示,∠ACB=90°,AB=17,AC=15, ∠BCM=∠BAC,求sin∠BAC的值和点B到直线MC的距离.
知识点三已知一角一边解直角三形
典例5如图5所示,在△ABC中,∠B=90°,∠C=60°,BC=9.求AC、AB的长.
跟踪训练6.如图6所示,已知,Rt△ABC中,∠C=90°,∠A=30°,BC=3,D为AC点,∠BDC=45°,求AB的长
知识点四“化斜为直”,解直角三角形
典例7.如图7所示,在△ABC中,已知BC=8,∠B=60°,∠C=45°,求AB的长.
跟踪训练8.如图8,在△ABC中,∠A=30°,tanB=,AC=2,求AB的长.
知识点五“割补”构造直角三角形
典例9.如图9所示,在四边形ABCD中,AB=3,CD=1,∠A=60°,∠B=∠D=90°,求四边形ABCD的面积.
跟踪训练10.如图11所示,已知四边形ABCD中,∠ADC=60°,AD⊥BA,CD⊥BC,AB=30,BC=60 ,求四边形ABCD面积.
知识点六仰角、俯角问题
典例11.如图11所示,某高速公路建设中需要测量某条江的宽度AB,飞机上的测量人员在C处测得A,B两点的俯角分别为45° 和30°若飞机离地面的高度CH为1500米,且点H,A,B在同一水平直线上,则这条江的宽度AB为______米 .(结果保留根号)
跟踪训练12.如图,从楼AB的A处测得对面楼CD的顶部C的仰角为 37°,底部D的俯角为 45°,两楼的水平距离BD为32m,那么楼CD的高度约为______m.
(结果精确到1m,参考数据: sin37 ≈0.6; cos37 ≈0.8; ; tan37 ≈0.75)
知识点七方向角、坡角问题
典例13.如图13所示,湖心岛上有一凉亭 B,在凉亭 B的正东湖边有一棵大树 A,在湖边的 C处测得 B在北偏西45°方向上,测得 A在北偏东30°方向上,又测得 B、 C之间的距离为120米,则A、 B之间的距离是 米.(结果保留根号形式)
跟踪训练14.如图14所示,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为______海里.
跟踪训练如图15所示,水坝的横断面是梯形ABCD,其中BC平行于AD,背水坡AB的坡角∠BAD=45°,坝高BE=20米,汛期来临,为加大水坝的防洪强度,将坝底从A处向后水平延伸到F处,使新的背水坡BF的坡角∠F=30°,则AF为 米.(结果精确到1米,参考数据:≈1.414,≈1.732)
知识点八三角函数与一次函数的结合
典例16..如图16所示,直线y=kx-1与x轴、y轴分别交于B、C两点,tan∠OCB=.
求点B的坐标和一次函数表达式.
跟踪训练17.如图17所示,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=,B(m,﹣2).
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.
【巩固训练】
1.小丽同学在校外实践活动中对某一黄河大桥开展测量活动.如图19所示,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.+ D.atanα+atanβ
2.在平面直角坐标系中,将一块直角三角板如图20所示放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数y=﹣(x<0),y=(x>0)的图象上,则sin∠ABO的值= .
3.如图21所示的网格是正方形网格,则∠PAB+∠PBA= .(点A,B,P是网格线交点)
4.如图22所示,在矩形ABCD中,AB=3,BC=2,H是AB的中点,将△CBH沿CH折叠,点B落在矩形内点P处,连接AP,则tan∠HAP= .
5.如图23所示,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=在第一象限内的图象经过点D,交BC于点E.若AB=6,CE=2BE,tan∠AOD=,则k的值为 .
6.如图24所示,无人机于空中A处测得某建筑顶部B处的仰角为45°,测得该建筑底部C处的俯角为17°.若无人机的飞行高度AD为62m,则该建筑的高度BC为 m.
(参考数据:sin17°≈0.29,cos17°≈0.96,tan17°≈0.31)
7.如图25所示,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50米,某人在河岸MN的A处测得∠DAN=45°,然后沿河岸走了130米到达B处,测得∠CBN=60°.则河流的宽度CE为______.
8.如图26所示,在Rt△ABC中,∠C=90°,点D在BC边上,∠ADC=45°,BD=2,tanB=
求AC和AB的长; (2)求sin∠BAD的值.
9.如图27所示,某小岛B在港口A的南偏西63°方向上,某船从港口A出发沿北偏西72°的方向以每小时25海里的速度行驶了2小时到达C处,在C处测得小岛B在南偏西33°的方向上,求港口A与小岛B的距离
如图28所示,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为
(﹣2,0),且tan∠ACO=2.
求该反比例函数和一次函数的解析式;
(1)求点B的坐标;
(2)在x轴上求点E,使△ACE为直角三角形.(直接写出点E坐标)
直角三角形边角关系复习
【课堂练习】1.1, 2.3, 3.-7+,4.AB=6;∠A=30°;∠B=60°,5.sin∠BAC=;
MC=, 6.AC=18;AB=9 7.AD=3-3, 8.AB=8-1, 9.AB=5,
四边形ABCD面积=4 ,11. 四边形ABCD面积=4950 ,
12.(1500-1500), 14. (60+20),15.20, 15.56 16. 15,
17.B(,0);y=2x-1, 18.(1)y=x+1;y=,(2)x>2或-3
图1
h
l
i=h:l
α
图2 图3
图3 图4 图5 图6
图7 图8
图10
图9
图11
图12
图12 图13
图13 图14 图15
图16 图17
图19 图20 图21
图22 图23 图24
图25 图26 图27
图28
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
