第四章 投影与视图复习学案
图片预览


文档简介
中小学教育资源及组卷应用平台
投影与视图复习
【学习目标】
1.准确理解把握平行投影与中心投影的性质、三视图与几何体的相互转化,以及侧面展开图、面积、体积等与三视图有关的计算
【课前梳理】
有关概念
1.平行投影:由 形的投影.
2.中心投影:由 (点光源)发出的光线形的投影.
3.正投影:投影线 于投影面产生的投影.
三视图
位置:首先确定 的位置,画出主视图,然后在主视图的正右方画出左视图,在主视图的正下方画出俯视图.
虚实:在画图时,看得见的部分的轮廓线通常画成实线,看不见的部分的轮廓线通常画成
线.
大小:主视图与俯视图长对正,主视图与左视图 ,左视图与俯视图 .
【课堂练习】
知识点一投影的应用
典例1.如图1所示,为了测量图(1)和图(2)中的树高,在同一时刻某人进行了如下操作:
图(1):测得竹竿CD的长为1.2米,其影CE长1.6米,树影AE长2.4米.
图(2):测得落在地面的树影长2.8米,落在墙上的树影高1.5米,请问图(1)和图(2)中的树高各是多少
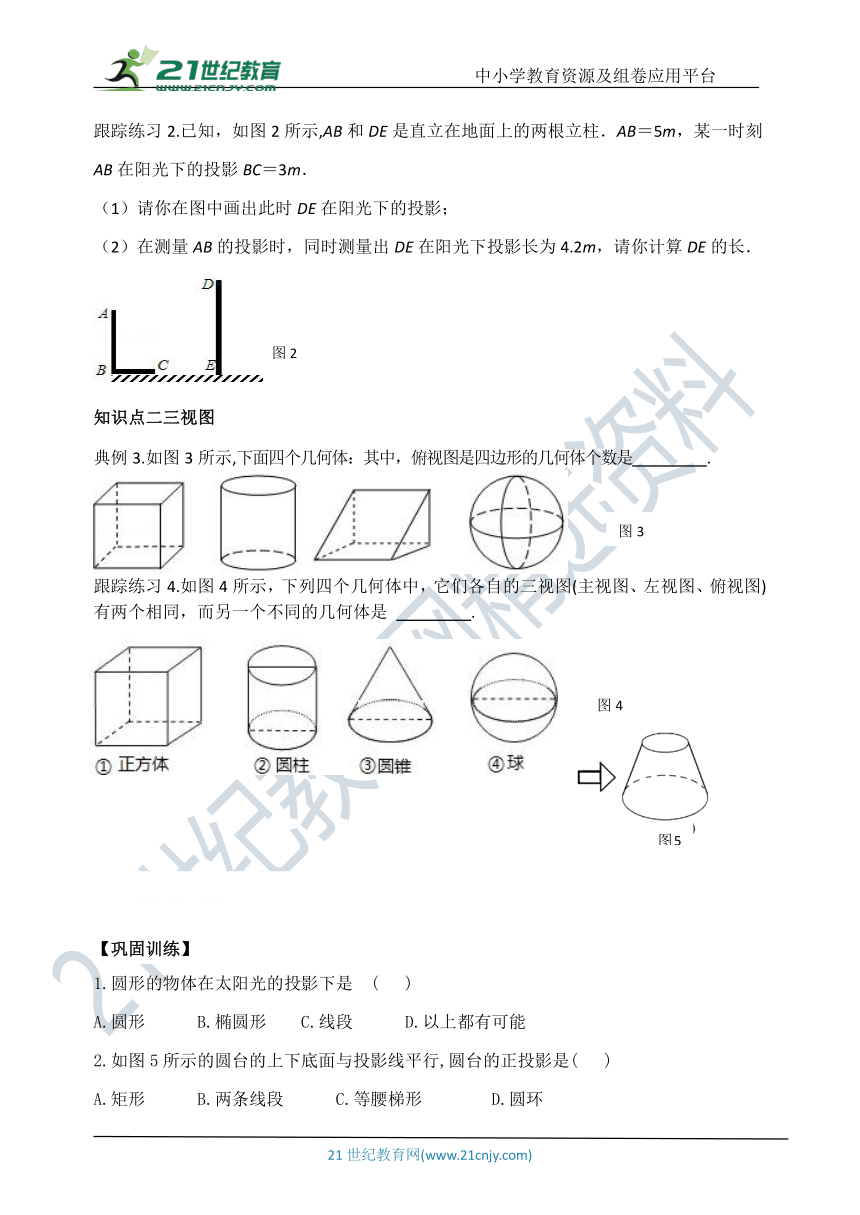
跟踪练习2.已知,如图2所示,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下投影长为4.2m,请你计算DE的长.
知识点二三视图
典例3.如图3所示,下面四个几何体:其中,俯视图是四边形的几何体个数是 .
跟踪练习4.如图4所示,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 .
【巩固训练】
1.圆形的物体在太阳光的投影下是 ( )
A.圆形 B.椭圆形 C.线段 D.以上都有可能
2.如图5所示的圆台的上下底面与投影线平行,圆台的正投影是( )
A.矩形 B.两条线段 C.等腰梯形 D.圆环
3.如图6所示,摆放的几何体的左视图是 ( )
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
5.小明在操场上练习双杠时,在练习的过程中他发现在地上双杠的两横杠的影子( )
A.相交 B.平行 C.垂直 D.无法确定
6.在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是 ( )
A.上午 B.中午 C.下午 D.无法确定
7.如图7是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
A.①②③④ B.④①③② C.④②③① D.④③②①
8.如图8所示,是下列哪个几何体的主视图与俯视图( )
9.如图9所示,下列图形中,主视图为图①的是( )
10.如图10所示,下列几何体中,主视图与俯视图不相同的是( )
11.如图11所示,是由长方体和圆柱组成的几何体,它的俯视图是( )
12.如图12所示的工件,其俯视图是( )
13.如图13所示,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
由一些相同的小立方块搭成的几何体的三视图如图14所示,则搭成该几何体的小立方块有 块.
如图15所示,是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是
cm2
16.(1)如图1是同一时刻的两棵树及其影子,请你在图中画出形成树影的光线,并判断它是太阳光线还是灯光的光线?若是灯光的光线,请确定光源的位置;
(2)请判断如图2所示的两棵树的影子是在太阳光下形成的,还是灯光下形成的?并画出同一时刻旗杆的影子(用线段表示).
17.如图是某工件的三视图,求此工件的表面积.
18.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.8m的小明落在地面上的影长为BC=3m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16.5m,请求出旗杆DE的高度.
投影与视图复习
【课堂练习】1.1.8米;2.4米.2.解答:
(1)如图所示:EF即为所求;
(2)∵AB=5m,某一时刻AB在阳光下的投影BC=3m,EF=4.2m,
∴=,则= 解得:DE=7, 答:DE的长为7m.
3.2 , 4.②③,
【巩固训练】1.D, 2.C, 3.C, 4.D, 5.B, 6.A, 7.B, 8.D, 9.A, 10.B
11.A, 12.B, 13.C, 14.4, 15.200Π,
16.解:(1)如图1所示是灯光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及其影子的顶端作一条直线,两直线相交,其交点就是光源的位置;
(2)如图2所示,是太阳光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及其影子的顶端作一条直线,两直线平行.然后再过旗杆的顶端作一条与已知光线平行的直线,交地面于一点,连接这点与旗杆底端的线段就是旗杆的影子.
17.24ΠC㎡,
18.解:(1)影子EG如图所示;
(2)∵DG∥AC, ∴∠G=∠C, ∴Rt△ABC∽△Rt△DGE,
∴=,即=,解得DE=, ∴旗杆的高度为m.
图1
图2
图3
图4
图5
图6
图7
B. C. D. 图8
A. B. C. D. 图9
A. B. C. D. 图10
A. B. C. D. 图11
A. B. C. D. 图12
A. B. C. D. 图13
图14 图15
图16
图17
图18
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
投影与视图复习
【学习目标】
1.准确理解把握平行投影与中心投影的性质、三视图与几何体的相互转化,以及侧面展开图、面积、体积等与三视图有关的计算
【课前梳理】
有关概念
1.平行投影:由 形的投影.
2.中心投影:由 (点光源)发出的光线形的投影.
3.正投影:投影线 于投影面产生的投影.
三视图
位置:首先确定 的位置,画出主视图,然后在主视图的正右方画出左视图,在主视图的正下方画出俯视图.
虚实:在画图时,看得见的部分的轮廓线通常画成实线,看不见的部分的轮廓线通常画成
线.
大小:主视图与俯视图长对正,主视图与左视图 ,左视图与俯视图 .
【课堂练习】
知识点一投影的应用
典例1.如图1所示,为了测量图(1)和图(2)中的树高,在同一时刻某人进行了如下操作:
图(1):测得竹竿CD的长为1.2米,其影CE长1.6米,树影AE长2.4米.
图(2):测得落在地面的树影长2.8米,落在墙上的树影高1.5米,请问图(1)和图(2)中的树高各是多少
跟踪练习2.已知,如图2所示,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下投影长为4.2m,请你计算DE的长.
知识点二三视图
典例3.如图3所示,下面四个几何体:其中,俯视图是四边形的几何体个数是 .
跟踪练习4.如图4所示,下列四个几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是 .
【巩固训练】
1.圆形的物体在太阳光的投影下是 ( )
A.圆形 B.椭圆形 C.线段 D.以上都有可能
2.如图5所示的圆台的上下底面与投影线平行,圆台的正投影是( )
A.矩形 B.两条线段 C.等腰梯形 D.圆环
3.如图6所示,摆放的几何体的左视图是 ( )
4.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下 ( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
5.小明在操场上练习双杠时,在练习的过程中他发现在地上双杠的两横杠的影子( )
A.相交 B.平行 C.垂直 D.无法确定
6.在一个晴朗的好天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是 ( )
A.上午 B.中午 C.下午 D.无法确定
7.如图7是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
A.①②③④ B.④①③② C.④②③① D.④③②①
8.如图8所示,是下列哪个几何体的主视图与俯视图( )
9.如图9所示,下列图形中,主视图为图①的是( )
10.如图10所示,下列几何体中,主视图与俯视图不相同的是( )
11.如图11所示,是由长方体和圆柱组成的几何体,它的俯视图是( )
12.如图12所示的工件,其俯视图是( )
13.如图13所示,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
由一些相同的小立方块搭成的几何体的三视图如图14所示,则搭成该几何体的小立方块有 块.
如图15所示,是按1:10的比例画出的一个几何体的三视图,则该几何体的侧面积是
cm2
16.(1)如图1是同一时刻的两棵树及其影子,请你在图中画出形成树影的光线,并判断它是太阳光线还是灯光的光线?若是灯光的光线,请确定光源的位置;
(2)请判断如图2所示的两棵树的影子是在太阳光下形成的,还是灯光下形成的?并画出同一时刻旗杆的影子(用线段表示).
17.如图是某工件的三视图,求此工件的表面积.
18.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.8m的小明落在地面上的影长为BC=3m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;
(2)若小明测得此刻旗杆落在地面的影长EG=16.5m,请求出旗杆DE的高度.
投影与视图复习
【课堂练习】1.1.8米;2.4米.2.解答:
(1)如图所示:EF即为所求;
(2)∵AB=5m,某一时刻AB在阳光下的投影BC=3m,EF=4.2m,
∴=,则= 解得:DE=7, 答:DE的长为7m.
3.2 , 4.②③,
【巩固训练】1.D, 2.C, 3.C, 4.D, 5.B, 6.A, 7.B, 8.D, 9.A, 10.B
11.A, 12.B, 13.C, 14.4, 15.200Π,
16.解:(1)如图1所示是灯光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及其影子的顶端作一条直线,两直线相交,其交点就是光源的位置;
(2)如图2所示,是太阳光的光线.原因是过一棵树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及其影子的顶端作一条直线,两直线平行.然后再过旗杆的顶端作一条与已知光线平行的直线,交地面于一点,连接这点与旗杆底端的线段就是旗杆的影子.
17.24ΠC㎡,
18.解:(1)影子EG如图所示;
(2)∵DG∥AC, ∴∠G=∠C, ∴Rt△ABC∽△Rt△DGE,
∴=,即=,解得DE=, ∴旗杆的高度为m.
图1
图2
图3
图4
图5
图6
图7
B. C. D. 图8
A. B. C. D. 图9
A. B. C. D. 图10
A. B. C. D. 图11
A. B. C. D. 图12
A. B. C. D. 图13
图14 图15
图16
图17
图18
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
