8.4 机械能守恒定律 课件 (共26张PPT) 高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 8.4 机械能守恒定律 课件 (共26张PPT) 高一下学期物理人教版(2019)必修第二册 |  | |
| 格式 | zip | ||
| 文件大小 | 10.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-27 21:20:09 | ||
图片预览







文档简介
(共26张PPT)
必修二
8.4 机械能守恒定律
01
追寻守恒量
动能和势能的转化
机械能守恒定律
02
03
目录
C O N T E N T S
伽利略理想斜面实验
现象:在摩擦与空气阻力较小时,小球总能到达右侧与时放点基本等高的位置
假设推理:若忽略一切阻力,则小球能到达与释放点等高的位置
理想实验法(事实+推理)
A
B
h
h'
无论斜面 B 比斜面A 陡些或缓些,小球的速度最后总会在斜面上的某点变为 0,这点距斜面底端的竖直高度与它出发时的高度基本相同。这说明某种“东西”在小球运动的过程中是不变的。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
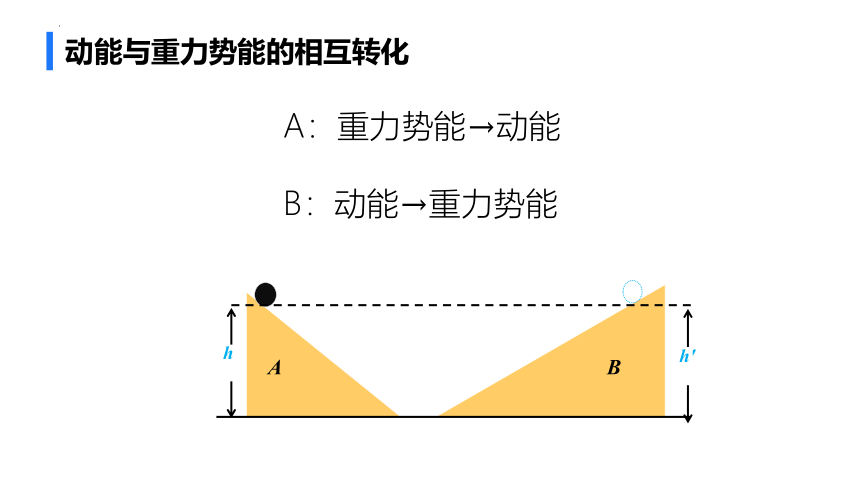
动能与重力势能的相互转化
A
B
h
h'
A:重力势能→动能
B:动能→重力势能
动能与弹性势能的相互转化
v=6m/s
v=0
向左:动能→弹性势能
向右:弹性势能→动能
运动员从跳板上弹起的过程中,跳板的弹性势能转化为运动员的动能。射箭是弓的弹性势能转化成箭的动能。
机械能
1、定义:重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
2、表达式: E=Ek+Ep
3、理解:标量(由正负)、状态量、相对量
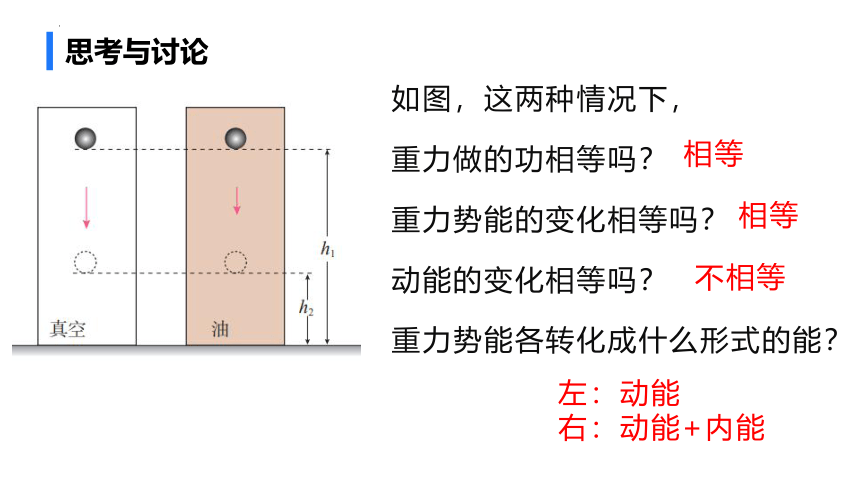
思考与讨论
如图,这两种情况下,
重力做的功相等吗?
重力势能的变化相等吗?
动能的变化相等吗?
重力势能各转化成什么形式的能?
相等
相等
不相等
左:动能
右:动能+内能
A点:动能为Ek1,重力势能为Ep1
B点:动能为Ek2,重力势能为Ep2
判断物体在A点的机械能 E1 和在B点的机械能 E2 的关系
由动能定理:
G
FN
只有重力作功的情况下,物体的机械能总量保持不变
光滑的曲面
机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,物体的动能
和势能可以相互转化,而总的机械能保持不变。
2.表达式:
(1)E1=E2 → EK2+EP2=EK1+EP1 →
或 ΔEk减=ΔEp增
(2)ΔEk= -ΔEp
或 ΔEA减=ΔEB增
(3)ΔEA= -ΔEB
守恒观点
转化观点
转移观点
3.条件:物体系统内只有重力或弹力做功(其他力不做功),
机械能守恒。(此处弹力高中阶段特指弹簧类弹力)
对条件的理解:
不受其他力
受其他力,但其他力不做功
受其他力,但其他力做功的代数和为零
守恒的判断方法
(1)做功分析法
(2)能量分析法
解题步骤
确定研究对象
受力分析
判定各个力是否做功,分析是否符合机械能守恒的条件
选取零势能参考面,确定始、末状态机械能
选择机械能哪种公式,列出方程求解
【例】把一个小球用细线悬挂起来,就成为一个摆(如图),摆长为l ,最大偏角为θ。如果阻力可以忽略,小球运动到最低位置时的速度大小是多少?
θ
机械能守恒定律与动能定理异同
机械能守恒定律 动能定理
不同点 需要判断是否满足守恒条件及确定零势能面 一般不考虑适用条件也不需要确定参考面
相同点 只需考虑初、末状态,不用考虑中间过程
应用 范围 能用机械能守恒定律解决的问题都能用动能定理解决;能用动能定理解决的问题不一定能用机械能守恒定律解决。
结论 动能定理比机械能守恒定律应用更广泛,更普遍
功能关系
1.功与能的关系:功是能量转化的量度,某种力做功往往与某一种具体形式的能量转化相联系,做了多少功,就有多少能量发生转化.
2.具体关系如下表:
功 能量转化 关系式
重力做功 重力势能的改变 WG=-ΔEp
弹力做功 弹性势能的改变 W弹=-ΔEp
合外力做功 动能的改变 W合=ΔEk
除系统内重力、弹力以外的其他力做功 机械能的改变 W=ΔE机
一对滑动摩擦力做功 机械能转化为内能 Ff·x相对=Q
小结
LOREM IPSUM DOLOR SIT AMET, CONSECTETUR ADIPISICING ELIT, SED DO EIUSMOD TEMPOR INCIDIDUNT UT LABORE ET DOLORE MAGNA ALIQUA. UT ENIM AD MINIM VENIAM
追寻守恒量
动能与势能的相互转化
机械能守恒定律
物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
动能、重力势能和弹性势能之间均可以相互转化。
在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
守恒条件:物体系统内只有重力或弹力做功,机械能守恒。
作业
thank you for watching
以下说法正确的是( )
A.物体所受的合外力为零,它的机械能一定守恒
B.物体做匀速运动,它的机械能一定守恒
C.物体所受的合外力不为零,机械能可能守恒
D.物体所受合外力做的功为零,它一定保持静止或匀速直线运动
C
含有弹簧的机械能守恒
(多选)如图所示,一根轻弹簧下端固定,竖立在水平面上.其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在小球下降阶段,下列说法中正确的是(不计空气阻力) ( )
A.在B位置小球动能最大
B.在C位置小球动能最大
C.从A→C位置小球重力势能的减少等于小球动能的增加
D.整个过程中小球和弹簧组成的系统机械能守恒
BD
一小球从地面以30m/s的速度竖直上抛,能上升的最大高度是多少?当重力势能是动能的一半时,高度是多少?(不计空气阻力,g=10m/s2 )
解:以地面为参考面,只有重力做功,机械能守恒:
当重力势能是动能的一半时:
h
v0
如图所示,粗细均匀的U形管内装有总长为4L的水,开始时阀门闭合,左右支管内水面高度差为L。打开阀门K后,当左右水面刚好相平时,左管液面的速度是多大?(摩擦力忽略不计)
解:设水的总质量为M,则由机械能守恒:
如图,轻弹簧一端与墙相连处于自然状态,质量为4kg的木块沿光滑的水平面以5 m/s的速度运动并开始挤压弹簧,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
答案:(1)50J,(2)32J
系统机械能守恒
如图,一固定的楔形木块,倾角θ=300,顶上有一定滑轮。细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升。物块A与斜面间无摩擦。当A沿斜面下滑 x 距离后,细线突然断了。求物块B上升离地的最大高度H.
解:以地面为参考面,则
细线断后B做竖直上抛运动,由机械能守恒定律得
θ
B
A
系统机械能守恒
如图,质量均为m的小球A、B固定在轻杆上,杆长L,OA=AB。轻杆由水平位置静止释放,当两小球运动到最低点时,求两小球速度各为多少.
解: 机械能守恒:
vA
vB
必修二
8.4 机械能守恒定律
01
追寻守恒量
动能和势能的转化
机械能守恒定律
02
03
目录
C O N T E N T S
伽利略理想斜面实验
现象:在摩擦与空气阻力较小时,小球总能到达右侧与时放点基本等高的位置
假设推理:若忽略一切阻力,则小球能到达与释放点等高的位置
理想实验法(事实+推理)
A
B
h
h'
无论斜面 B 比斜面A 陡些或缓些,小球的速度最后总会在斜面上的某点变为 0,这点距斜面底端的竖直高度与它出发时的高度基本相同。这说明某种“东西”在小球运动的过程中是不变的。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
动能与重力势能的相互转化
A
B
h
h'
A:重力势能→动能
B:动能→重力势能
动能与弹性势能的相互转化
v=6m/s
v=0
向左:动能→弹性势能
向右:弹性势能→动能
运动员从跳板上弹起的过程中,跳板的弹性势能转化为运动员的动能。射箭是弓的弹性势能转化成箭的动能。
机械能
1、定义:重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
2、表达式: E=Ek+Ep
3、理解:标量(由正负)、状态量、相对量
思考与讨论
如图,这两种情况下,
重力做的功相等吗?
重力势能的变化相等吗?
动能的变化相等吗?
重力势能各转化成什么形式的能?
相等
相等
不相等
左:动能
右:动能+内能
A点:动能为Ek1,重力势能为Ep1
B点:动能为Ek2,重力势能为Ep2
判断物体在A点的机械能 E1 和在B点的机械能 E2 的关系
由动能定理:
G
FN
只有重力作功的情况下,物体的机械能总量保持不变
光滑的曲面
机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,物体的动能
和势能可以相互转化,而总的机械能保持不变。
2.表达式:
(1)E1=E2 → EK2+EP2=EK1+EP1 →
或 ΔEk减=ΔEp增
(2)ΔEk= -ΔEp
或 ΔEA减=ΔEB增
(3)ΔEA= -ΔEB
守恒观点
转化观点
转移观点
3.条件:物体系统内只有重力或弹力做功(其他力不做功),
机械能守恒。(此处弹力高中阶段特指弹簧类弹力)
对条件的理解:
不受其他力
受其他力,但其他力不做功
受其他力,但其他力做功的代数和为零
守恒的判断方法
(1)做功分析法
(2)能量分析法
解题步骤
确定研究对象
受力分析
判定各个力是否做功,分析是否符合机械能守恒的条件
选取零势能参考面,确定始、末状态机械能
选择机械能哪种公式,列出方程求解
【例】把一个小球用细线悬挂起来,就成为一个摆(如图),摆长为l ,最大偏角为θ。如果阻力可以忽略,小球运动到最低位置时的速度大小是多少?
θ
机械能守恒定律与动能定理异同
机械能守恒定律 动能定理
不同点 需要判断是否满足守恒条件及确定零势能面 一般不考虑适用条件也不需要确定参考面
相同点 只需考虑初、末状态,不用考虑中间过程
应用 范围 能用机械能守恒定律解决的问题都能用动能定理解决;能用动能定理解决的问题不一定能用机械能守恒定律解决。
结论 动能定理比机械能守恒定律应用更广泛,更普遍
功能关系
1.功与能的关系:功是能量转化的量度,某种力做功往往与某一种具体形式的能量转化相联系,做了多少功,就有多少能量发生转化.
2.具体关系如下表:
功 能量转化 关系式
重力做功 重力势能的改变 WG=-ΔEp
弹力做功 弹性势能的改变 W弹=-ΔEp
合外力做功 动能的改变 W合=ΔEk
除系统内重力、弹力以外的其他力做功 机械能的改变 W=ΔE机
一对滑动摩擦力做功 机械能转化为内能 Ff·x相对=Q
小结
LOREM IPSUM DOLOR SIT AMET, CONSECTETUR ADIPISICING ELIT, SED DO EIUSMOD TEMPOR INCIDIDUNT UT LABORE ET DOLORE MAGNA ALIQUA. UT ENIM AD MINIM VENIAM
追寻守恒量
动能与势能的相互转化
机械能守恒定律
物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
动能、重力势能和弹性势能之间均可以相互转化。
在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
守恒条件:物体系统内只有重力或弹力做功,机械能守恒。
作业
thank you for watching
以下说法正确的是( )
A.物体所受的合外力为零,它的机械能一定守恒
B.物体做匀速运动,它的机械能一定守恒
C.物体所受的合外力不为零,机械能可能守恒
D.物体所受合外力做的功为零,它一定保持静止或匀速直线运动
C
含有弹簧的机械能守恒
(多选)如图所示,一根轻弹簧下端固定,竖立在水平面上.其正上方A位置有一只小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在小球下降阶段,下列说法中正确的是(不计空气阻力) ( )
A.在B位置小球动能最大
B.在C位置小球动能最大
C.从A→C位置小球重力势能的减少等于小球动能的增加
D.整个过程中小球和弹簧组成的系统机械能守恒
BD
一小球从地面以30m/s的速度竖直上抛,能上升的最大高度是多少?当重力势能是动能的一半时,高度是多少?(不计空气阻力,g=10m/s2 )
解:以地面为参考面,只有重力做功,机械能守恒:
当重力势能是动能的一半时:
h
v0
如图所示,粗细均匀的U形管内装有总长为4L的水,开始时阀门闭合,左右支管内水面高度差为L。打开阀门K后,当左右水面刚好相平时,左管液面的速度是多大?(摩擦力忽略不计)
解:设水的总质量为M,则由机械能守恒:
如图,轻弹簧一端与墙相连处于自然状态,质量为4kg的木块沿光滑的水平面以5 m/s的速度运动并开始挤压弹簧,求:
(1)弹簧的最大弹性势能;
(2)木块被弹回速度增大到3 m/s时弹簧的弹性势能。
答案:(1)50J,(2)32J
系统机械能守恒
如图,一固定的楔形木块,倾角θ=300,顶上有一定滑轮。细线跨过定滑轮,两端分别与物块A和B连结,A的质量为4m,B的质量为m,开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升。物块A与斜面间无摩擦。当A沿斜面下滑 x 距离后,细线突然断了。求物块B上升离地的最大高度H.
解:以地面为参考面,则
细线断后B做竖直上抛运动,由机械能守恒定律得
θ
B
A
系统机械能守恒
如图,质量均为m的小球A、B固定在轻杆上,杆长L,OA=AB。轻杆由水平位置静止释放,当两小球运动到最低点时,求两小球速度各为多少.
解: 机械能守恒:
vA
vB
